Giải bài 1 tr 18 sách GK Toán GT lớp 12
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau:
a) \(y = 2x^3 + 3x^2 - 36x - 10\).
b) \(y = x^4+ 2x^2 - 3\).
c) \(y = x + \frac{1}{x}\).
d) \(y = x^3(1 - x)^2\).
e) \(y = \sqrt {x^2-x+1}\).
Hướng dẫn giải chi tiết bài 1
Phương pháp giải:
Để giải bài 1 các em cần ôn lại các bước tìm cực trị bằng quy tắc 1:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Lời giải:
Áp dụng các bước trên ta tiến hành giải các câu a, b, c, d, e của bài 1 như sau:
Câu a:
Xét hàm số \(y = 2x^3 + 3x^2 - 36x - 10\)
Tập xác định: \(D=\mathbb{R}\).
Ta có đạo hàm: \(y' = 6{x^2} + 6x - 36\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 2\\ x = - 3 \end{array} \right.\)
Với x=2 ta có y=-54.
Với x=-3 ta có y=71.
Bảng biến thiên:
.png)
Hàm số đạt cực đại tại x=-3, giá trị cực đại ycđ = y(-3) = 71.
Hàm số đạt cực tiểu tại x = 2 , giá trị cực tiểu yct=y(2) =- 54.
Câu b:
Xét hàm số \(y = x^4+ 2x^2 - 3\)
Tập xác định: \(D=\mathbb{R}\).
Đạo hàm: \(y' = 4{x^3} + 4x = 4x({x^2} + 1)\)
\(y' = 0 \Leftrightarrow x = 0\)
Với x=0 ta có y=-3.
Bảng biến thiên của hàm số:
.png)
Hàm số đạt cực tiểu tại x=0, giá trị cực tiểu yct=y(0)=- 3.
Hàm số không có cực đại.
Câu c:
Xét hàm số \(y = x + \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
\(y'=1-\frac{1}{x^2}=\frac{x^2-1}{x^2}=\frac{(x-1)(x+1)}{x^2}\)
\(y' = 0 \Leftrightarrow (x - 1)(x + 1) = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 1 \end{array} \right.\)
Với x=1 ta có y=2.
Với x=-1 ta có y=-2.
Bảng biến thiên:
.png)
Hàm số đạt cực đại tại x=-1, giá trị cực đại ycđ = y(-1) = -2.
Hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu yct = y(1) = 2.
Câu d:
Xét hàm số \(y = x^3(1 - x)^2\)
Tập xác định: \(D=\mathbb{R}\).
Đạo hàm: \(y' = 3{x^2}{(1 - x)^2} - 2{x^3}(1 - x) \)
\(= {x^2}(1 - x)(3 - 5x)\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = \frac{3}{5}\\ x = 0 \end{array} \right.\)
Với \(x=1\) ta có \(y=0.\)
Với \(x=\frac{3}{5}\) ta có \(y=\frac{108}{3125}.\)
Với x=0 ta có \(y=0.\)
Bảng biến thiên:
.png)
Hàm số đạt cực đại tại \(x=\frac{3}{5},\) giá trị cực đại \(y_{cd} =y\left ( \frac{3}{5} \right )\frac{108}{3125}.\)
Hàm số đạt cực tiểu tại \(x=1,\) giá trị cực tiểu \(y_{ct}=y(1)=0.\)
Câu e:
Xét hàm số \(y = \sqrt {x^2-x+1}\)
Tập xác định: \(D=\mathbb{R}\).
Đạo hàm:
\({y' = \frac{{2x - 1}}{{2\sqrt {{x^2} - x + 1} }}}\)
\({y' = 0 \Leftrightarrow 2x - 1 = 0 \Leftrightarrow x = \frac{1}{2}}\)
Với \(x=\frac{1}{2}\) ta có \(y=\frac{\sqrt 3}{2}\).
Bảng biến thiên:
.png)
Vậy hàm số đạt cực tiểu tại \(x=\frac{1}{2}\), giá trị cực tiểu \(y_{ct}=y\left ( \frac{1}{2} \right )=\frac{\sqrt 3}{2}.\)
-- Mod Toán 12 HỌC247
-


Tìm cực trị của hàm số: (y={x}^{6}{(1-x)}^{5})?
bởi Nguyen Ngoc Anh
 13/09/2023
13/09/2023
1) \(y={x}^{6}{(1-x)}^{5}\) (định lý 1,2)
2) \(y=2cos2x+1\) (định lý 2)
Theo dõi (1) 0 Trả lời -


Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
bởi Sam sung
 15/05/2023
15/05/2023

Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( \sin x-\cos x \right)=m-1\) có hai nghiệm phân biệt trên khoảng \(\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\)?
A. \(13\). B. \(12\). C. \(11\). D. \(21\).
Theo dõi (0) 1 Trả lời -


Cho hàm đa thức bậc ba \(y=f\left( x \right)\) liên tục, có đạo hàm trên \(\left[ -2;2 \right]\) và có đồ thị như hình vẽ
bởi Kieu Oanh
 12/05/2023
12/05/2023
Cho hàm đa thức bậc ba \(y=f\left( x \right)\) liên tục, có đạo hàm trên \(\left[ -2;2 \right]\) và có đồ thị như hình vẽ
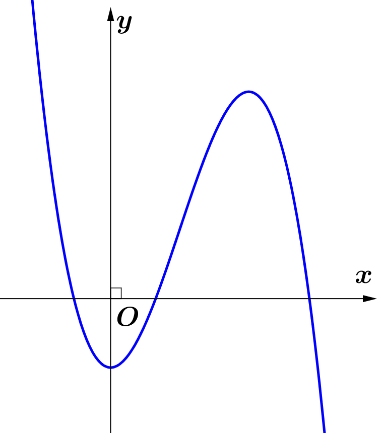
Số điểm cực tiểu của hàm số \(y=\sqrt[3]{{{\left( f\left( x \right) \right)}^{2}}}\) là
A. 1.
B. 2.
C. 3.
D. 5.
Theo dõi (0) 1 Trả lời -


Hyax tìm các hệ số a, b, c sao cho hàm số: \(f(x) = {x^3} + a{x^2} + bx + c\) đạt cực tiểu tại điểm \(x = 1,{\rm{ }}f\left( 1 \right) = - 3\) và đồ thị của hàm số cắt trục tung tại điểm có tung độ là 2.
bởi Hương Lan
 18/10/2022
Theo dõi (0) 1 Trả lời
18/10/2022
Theo dõi (0) 1 Trả lời -


Thực hiện tìm cực trị hàm số sau: \(y = 2\sin x + {\rm{cos2}}x;x \in \left[ {0;\pi } \right]\)
bởi Co Nan
 19/10/2022
Theo dõi (0) 1 Trả lời
19/10/2022
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho biết hàm số \(y = {x^3} + \dfrac{3}{2}{x^2}\). Khoảng cách \(d\) giữa hai điểm cực trị của đồ thị hàm số là:
bởi Mai Thuy
 19/09/2022
Theo dõi (0) 1 Trả lời
19/09/2022
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để hàm số sau có cực trị: \(y = {x^3} - 3\left( {m - 1} \right){x^2} - 3\left( {m + 3} \right)x - 5\)
bởi Lê Tường Vy
 19/09/2022
Theo dõi (0) 1 Trả lời
19/09/2022
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để hàm số sau không có cực trị: \(y = \dfrac{1}{3}m{x^3} + m{x^2} + 2\left( {m - 1} \right)x - 2\)
bởi hành thư
 19/09/2022
Theo dõi (0) 1 Trả lời
19/09/2022
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = - {x^4} + 4{x^2} - 3\). Hàm số có bao nhiêu điểm cực đại, bao nhiêu điểm cực tiểu?
bởi Việt Long
 19/09/2022
Theo dõi (0) 1 Trả lời
19/09/2022
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để hàm số \(y = \dfrac{{{x^2} - 2mx + 5}}{{x - m}}\) có cực trị:
bởi Nguyễn Lê Tín
 19/09/2022
Theo dõi (0) 1 Trả lời
19/09/2022
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + mx - 5\) có cực trị:
bởi A La
 19/09/2022
Theo dõi (0) 1 Trả lời
19/09/2022
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Hàm số \(y = {\left( {x + 1} \right)^3}\left( {5 - x} \right)\) có mấy điểm cực trị?
bởi Van Dung
 20/09/2022
Theo dõi (0) 1 Trả lời
20/09/2022
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để hàm số sau không có cực trị: \(y = \dfrac{{{x^2} + 2mx - 3}}{{x - m}}\)
bởi Mai Bảo Khánh
 20/09/2022
Theo dõi (0) 1 Trả lời
20/09/2022
Theo dõi (0) 1 Trả lời -


Hãy xác định m để hàm số: \(y = {x^3} - m{x^2} + \left( {m - \dfrac{2}{3}} \right)x + 5\) có cực trị tại \(x = 1\). Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
bởi Bao Chau
 20/09/2022
Theo dõi (0) 1 Trả lời
20/09/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 18 SGK Giải tích 12
Bài tập 3 trang 18 SGK Giải tích 12
Bài tập 4 trang 18 SGK Giải tích 12
Bài tập 5 trang 18 SGK Giải tích 12
Bài tập 6 trang 18 SGK Giải tích 12
Bài tập 1.17 trang 15 SBT Toán 12
Bài tập 1.18 trang 15 SBT Toán 12
Bài tập 1.19 trang 16 SBT Toán 12
Bài tập 1.20 trang 16 SBT Toán 12
Bài tập 1.21 trang 16 SBT Toán 12
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





