Giải bài 1.21 tr 16 SBT Toán 12
Xác định giá trị của tham số m để hàm số sau có cực trị:
\(y = {x^3} + 2m{x^2} + mx - 1\).
Hướng dẫn giải chi tiết
TXĐ:
\(y' = 3{x^2} + 4mx + m\)
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên
\( \Leftrightarrow 3{x^2} + 4mx + m\) có hai nghiệm phân biệt
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\Leftrightarrow \Delta ' = 4{m^2} - 3m > 0\\
\Leftrightarrow m\left( {4m - 3} \right) > 0
\end{array}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m < 0}\\
{m > \frac{3}{4}}
\end{array}} \right.}
\end{array}\)
Vậy hàm số đã cho có cực đại, cực tiểu khi hoặc
-- Mod Toán 12 HỌC247
-


Tìm nguyên hàm của f(x)=tan²x-2x+1
bởi Nguyen Hung Anh
 12/01/2020
Nguyen ham cua ham f(x)=tan²x-2x 1Theo dõi (0) 0 Trả lời
12/01/2020
Nguyen ham cua ham f(x)=tan²x-2x 1Theo dõi (0) 0 Trả lời -


Hàm số f(x) có bao nhiêu điểm cực trị biết f'(x)=x^4.(x-1).(2-x)^3.(x-4)^2?
bởi Trịnh Thị Hạnh
 09/01/2020
09/01/2020
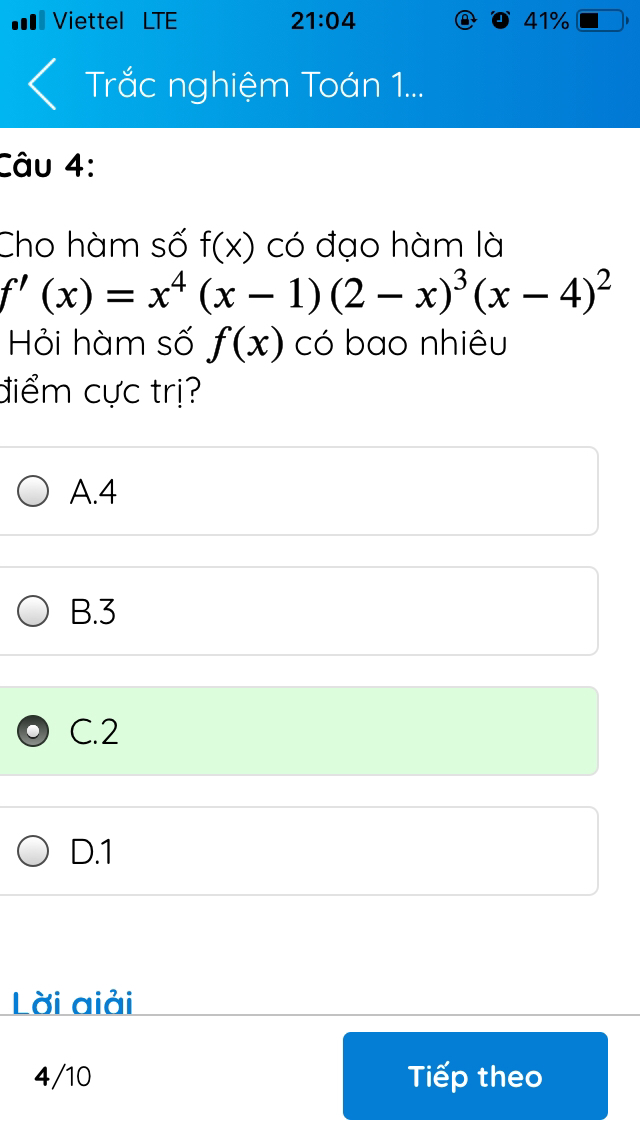 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


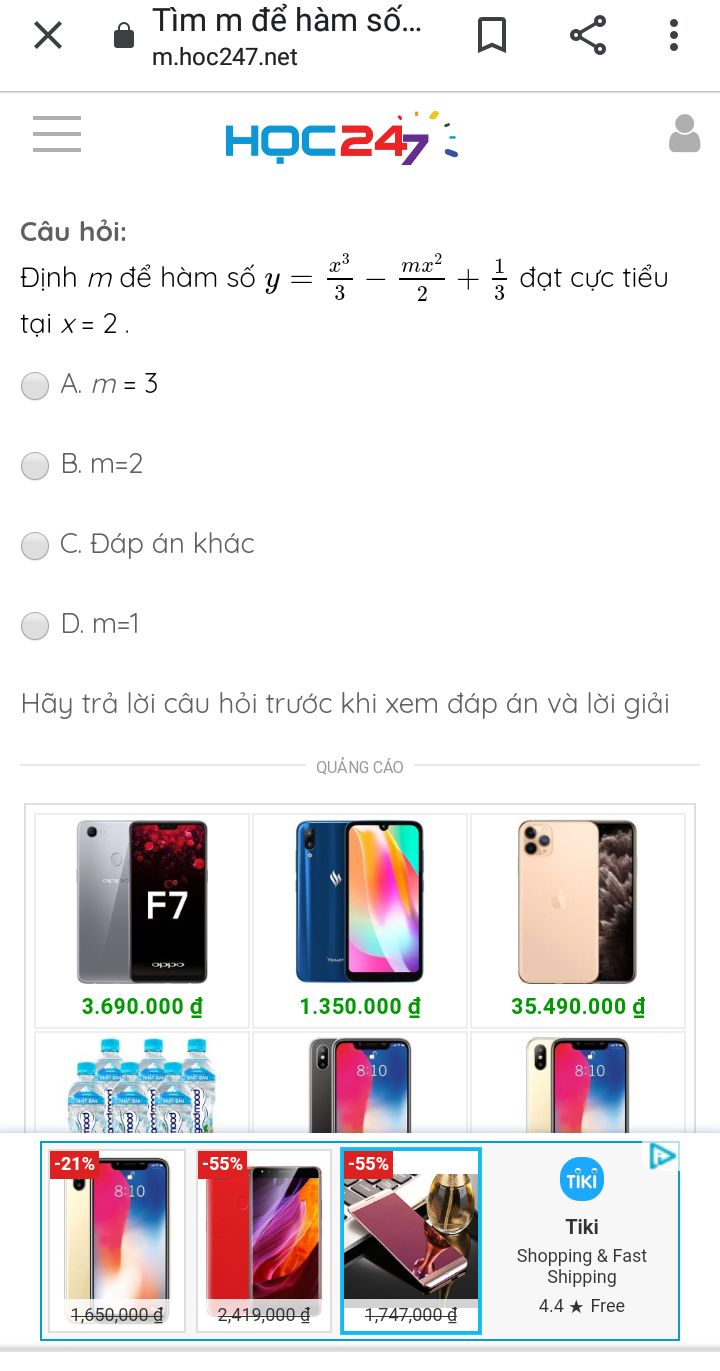 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm số điểm cực đại của hàm số có đạo hàm f'(x)=(x-1)^2.(x+3).(x-2).(x-3)^3
bởi Lê thị quỳnh nga
 30/12/2019
Giải hộ em câu 17 với ạ
30/12/2019
Giải hộ em câu 17 với ạ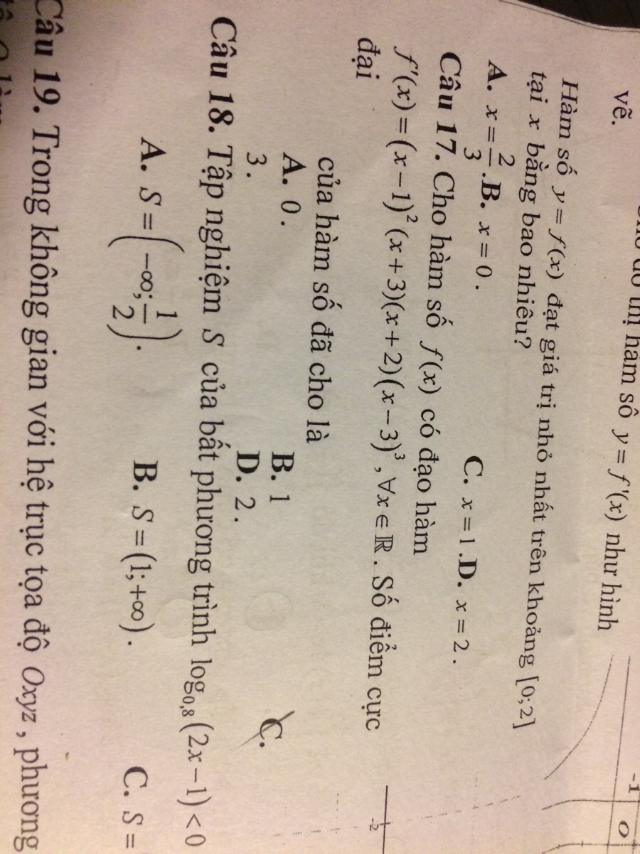 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để hàm số y=(x^2+mx+m^2-1)/x có cực trị
bởi Băng Như
 25/12/2019
25/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giá trị của P=3^a+2^b biết a, b(a < b) là các nghiệm của phương trình 6^x +6=2^(x 1) +3^(x +1)
bởi Hải Yến Nguyễn
 25/12/2019
25/12/2019
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Cách tìm cực trị bằng máy tính?
bởi Vũ Huế
 22/12/2019
Tìm cực trị bằng máy tínhTheo dõi (0) 3 Trả lời
22/12/2019
Tìm cực trị bằng máy tínhTheo dõi (0) 3 Trả lời -


Định m để hàm số y=1/3x^3-(m+1)x+m không có cực trị
bởi Mỹ DuyÊn
 22/12/2019
22/12/2019
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Hàm số y=(2-x)/(x+2) có tiệm cận ngang là?
bởi Vân Hồng Đặng
 19/12/2019
19/12/2019
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Hàm số y=x^4-2x^2+1 có bao nhiêu điểm cực trị?
bởi Nguyễn Thị Huệ
 18/12/2019
hàm số y=x^4-2x^2 1 có bao nhiêu điểm cực trịTheo dõi (0) 4 Trả lời
18/12/2019
hàm số y=x^4-2x^2 1 có bao nhiêu điểm cực trịTheo dõi (0) 4 Trả lời -


Tìm m để đoạn AB có độ dài nhỏ nhất biết đường thẳng d:y=-x+m luông cắt đồ thị hàm số tại 2 điểm phân biệt A, B
bởi Phạm Lan
 17/12/2019
17/12/2019
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tìm số nghiệm của phương trình 2f(x)-3=0
bởi Hero Duong
 17/12/2019
17/12/2019
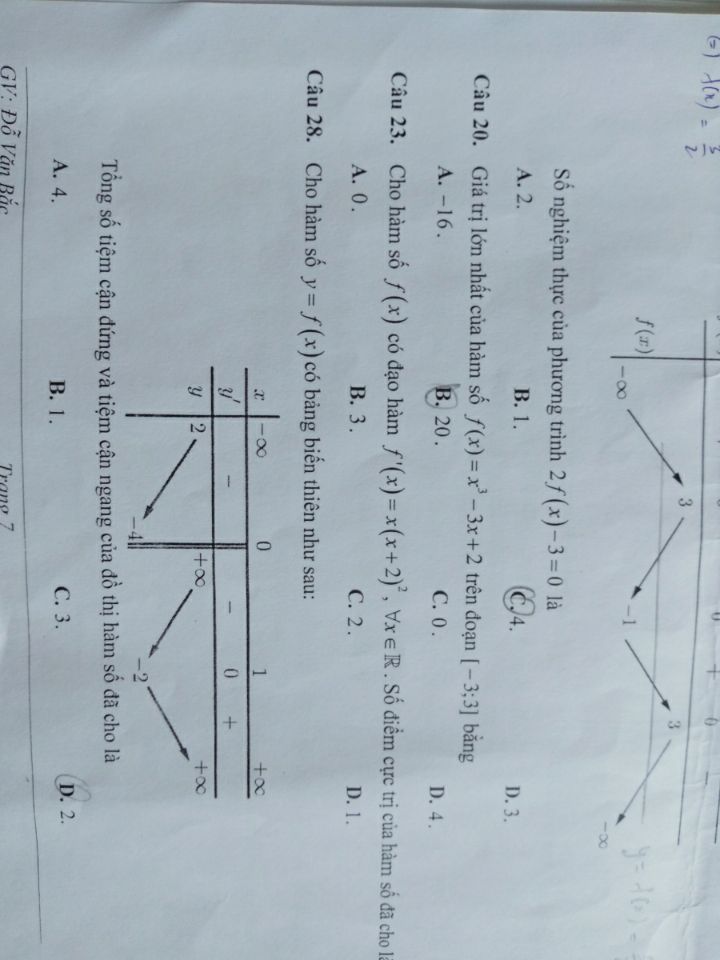 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tất cả các giá trị nguyên của m để hàm số y=(m-1)x^4-2(m-3)x^2+1 không có cực đại
bởi Trinh Cam
 17/12/2019
.
17/12/2019
.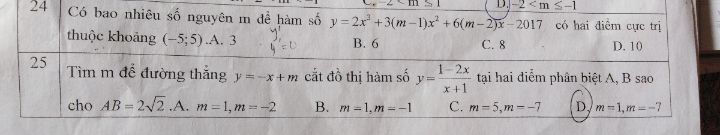 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Hàm số y=x^4+4x^2+3 đồng biến trên khoảng nào?
bởi Cẩm Đào
 15/12/2019
15/12/2019
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Hàm số nào sau đây có cực trị?
bởi Văn Thị Mỹ Tiên
 15/12/2019
Hàm số nào sau đây có cực trịTheo dõi (0) 1 Trả lời
15/12/2019
Hàm số nào sau đây có cực trịTheo dõi (0) 1 Trả lời -


Đồ thị hàm số y=(căn x+1)/căn(f(x)) có nhiều nhất bao nhiêu điểm cực trị?
bởi Nguyễn Văn Hoàng
 14/12/2019
Câu 37
14/12/2019
Câu 37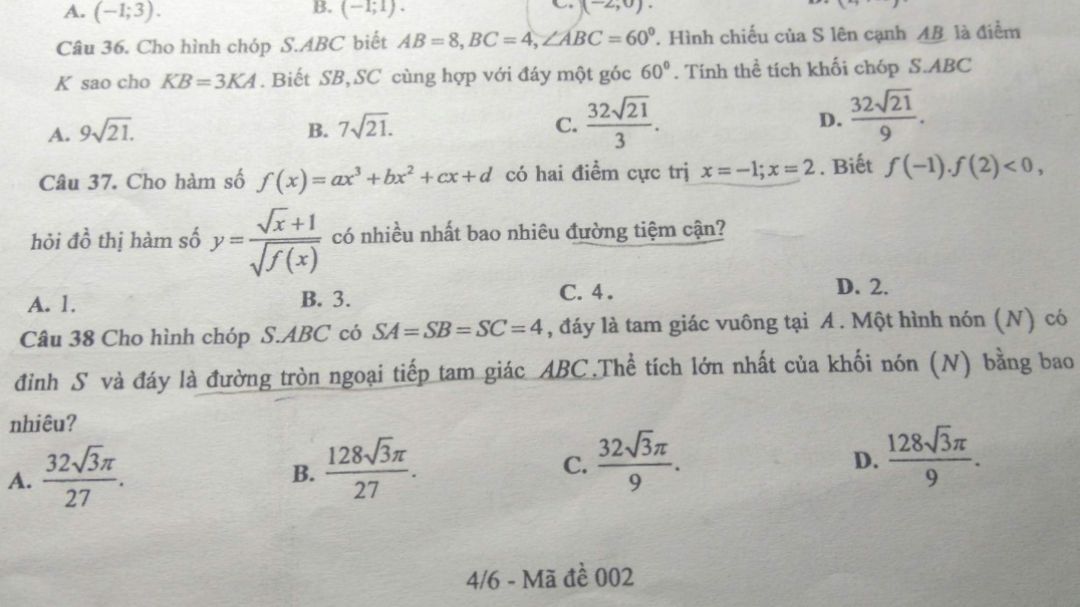 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 1.19 trang 16 SBT Toán 12
Bài tập 1.20 trang 16 SBT Toán 12
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





