Giải bài 1.20 tr 16 SBT Toán 12
Tìm cực trị của các hàm số sau:
a) ;
b) ;
c) .
Hướng dẫn giải chi tiết
a)
Hàm số có chu kì \(T = \pi \)
Xét hàm số trên đoạn \(\left[ {0;\pi } \right]\), ta có:
\(\begin{array}{l}
y' = 2\cos 2x\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{4}\\
x = \frac{{3\pi }}{4}
\end{array} \right.
\end{array}\)
Bảng biến thiên:
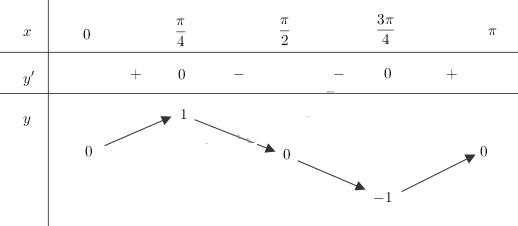
Do đó trên đoạn \(\left[ {0;\pi } \right]\), hàm số đạt cực đại tại \(\frac{\pi }{4}\), đạt cực tiểu tại \(\frac{{3\pi }}{4}\) và:
\(\begin{array}{l}
{y_{{\rm{CD}}}} = y\left( {\frac{\pi }{4}} \right) = 1;\\
{y_{CT}} = y\left( {\frac{{3\pi }}{4}} \right) = - 1
\end{array}\)
Vậy trên ta có:
\({y_{{\rm{CD}}}} = y\left( {\frac{\pi }{4} + k\pi } \right) = 1;\)
\({y_{CT}} = y\left( {\frac{{3\pi }}{4} + k\pi } \right) = - 1,\,k \in Z\)
b) \(y = \cos x - \sin x\). Hàm số tuần hoàn chu kì \(2\pi \) nên ta xét trên đoạn \(\left[ { - \pi ;\pi } \right]\)
\(\begin{array}{l}
y' = - \sin x - \cos x\\
y' = 0 \Leftrightarrow \tan x = - 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi ,k \in Z
\end{array}\)
Lập bảng biến thiên trên đoạn \(\left[ { - \pi ;\pi } \right]\)
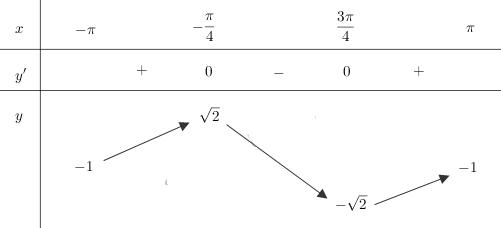
Hàm số đạt cực đại tại \(y = - \frac{\pi }{4} + k2\pi \), đạt cực tiểu tại \(y = \frac{{3\pi }}{4} + k2\pi \left( {k \in Z} \right)\) và
\(\begin{array}{l}
{y_{{\rm{CD}}}} = y\left( { - \frac{\pi }{4} + k2\pi } \right) = \sqrt 2 \\
{y_{CT}} = y\left( {\frac{{3\pi }}{4} + k2\pi } \right) = - \sqrt 2 \left( {k \in Z} \right)
\end{array}\)
c) Ta có \(y = {\sin ^2}x = \frac{{1 - \cos 2x}}{2}\)
Do đó, hàm số đã cho tuần hoàn theo chu kì \(\pi \). Ta xét hàm số \(y = \frac{1}{2} - \frac{1}{2}\cos 2x\) trên đoạn \(\left[ {0;\pi } \right]\)
\(\begin{array}{l}
y' = \sin 2x\\
y' = 0 \Leftrightarrow \sin 2x = 0 \Leftrightarrow x = k\frac{\pi }{2}\left( {k \in Z} \right)
\end{array}\)
Lập bảng biến thiên trên đoạn \(\left[ {0;\pi } \right]\)
.png)
Từ đó, ta thấy hàm số đạt cực tiểu tại \(x = k\frac{\pi }{2}\) với k chẵn, đạt cực đại tại \(x = k\frac{\pi }{2}\) với k lẻ, và \({y_{CT}} = y\left( {2m\pi } \right) = 0;\,\,{y_{{\rm{CD}}}} = y\left( {\left( {2m + 1} \right)\frac{\pi }{2}} \right) = 1\,\,\left( {m \in Z} \right)\)
-- Mod Toán 12 HỌC247
-


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính tổng M=a^2+b^2+c^2+d^2 biết đồ thị hàm số y=(3a^2-1)x^3-(b^3+1)x^2+3c^2x+4d có 2 điểm cực trị
bởi Nguyen Hong Duc
 19/04/2020
19/04/2020
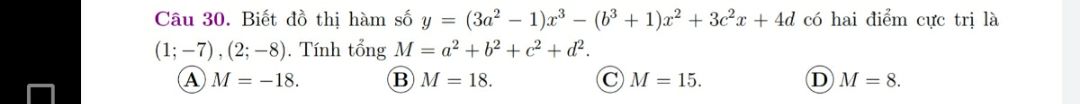 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Giải dùm mình với
Giải dùm mình với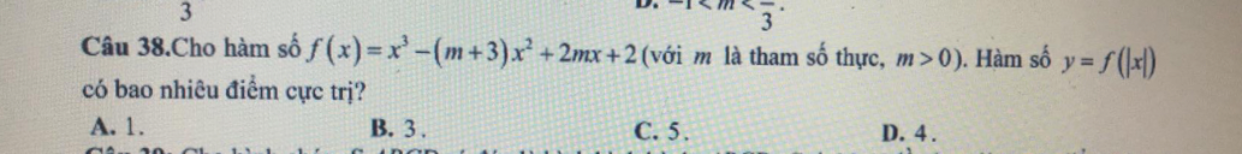 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cực trị dương của hàm số là gì
bởi Tran Hien Nhung
 17/04/2020
Cực trị dương của hàm số là gì ?Theo dõi (0) 2 Trả lời
17/04/2020
Cực trị dương của hàm số là gì ?Theo dõi (0) 2 Trả lời -

 Giải giúp câu 13 đi
Giải giúp câu 13 đi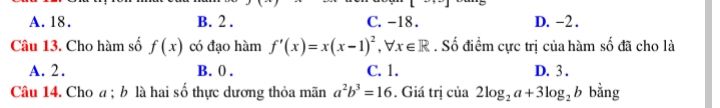 Theo dõi (1) 16 Trả lời
Theo dõi (1) 16 Trả lời -


y=mx^4+ (m-1)x +1-2m. tìm m để hàm số chỉ có duy nhất 1 cực trị
Theo dõi (0) 7 Trả lời -


Tìm tập hợp giá trị của tham số thực m để hàm số y=ln(x^2+1)-mx+1 đồng biến trên R
bởi Thương Võ
 23/03/2020
23/03/2020
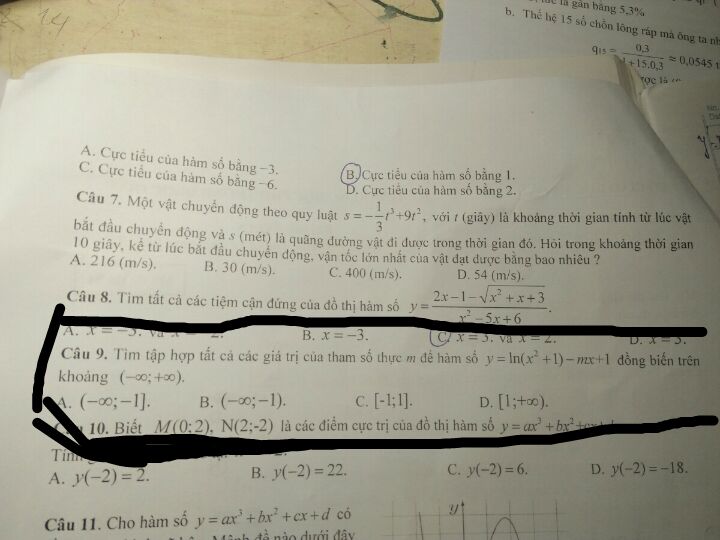 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm tất cả các giá trị của tham số m để đồ thị của hàm số y=x^3-2(mx)^2+1 có ba điểm cực trị tạo thahf một tam giác đều
bởi Hằng Mon
 18/03/2020
Tìm giá trị thực của than số
18/03/2020
Tìm giá trị thực của than số Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Hàm số y=x^4+2x^2+3 có bao nhiêu cực trị?
bởi Hiếu
 09/03/2020
09/03/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tất cả các giá trị thực của tham số m sao cho ddood thị của hàm số y=x⁴ 2mx² 1 có ba điểm cực trị tạo thành một tam giác vuông cân
bởi Otaku Nhi
 05/03/2020
tìm tất cả các giá trị thực của tham số m sao cho ddood thị của hàm số y=x⁴ 2mx² 1 có ba điểm cực trị tạo thành một tam giác vuông cânTheo dõi (0) 2 Trả lời
05/03/2020
tìm tất cả các giá trị thực của tham số m sao cho ddood thị của hàm số y=x⁴ 2mx² 1 có ba điểm cực trị tạo thành một tam giác vuông cânTheo dõi (0) 2 Trả lời -


Tìm a, b là các số thực sao cho điểm A(0;1) là điểm cực đại của đồ thị hàm số y=ax^2+a^2+b/(x+1)
bởi Lâm Hậu
 22/02/2020
ai giải dùm em câu 39 với ạ...càng chi tiết càng tốt
22/02/2020
ai giải dùm em câu 39 với ạ...càng chi tiết càng tốt Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Hàm số y=|x^2+3x-2| có bao nhiêu điểm cực trị?
bởi Trần Nụ
 22/02/2020
22/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tất cả các giá trị thực của m để hàm số y=x^3-3mx^2+(2m+1)x-m+5 có cực đại, cực tiểu
bởi Mặt Trời Nhỏ
 20/02/2020
20/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Hàm số y=f(x) liên tục trên R và f′(x)=(x−2)(x^2−1)^2 có số điểm cực trị là?
bởi Đức Mạnh
 17/02/2020
17/02/2020
Cho hàm số y=f(x)y=f(x) liên tục trên RR và f′(x)=(x−2)(x2−1)2f′(x)=(x−2)(x2−1)2. Hàm số có số điểm cực trị là
Theo dõi (0) 0 Trả lời -

 Giúp mk câu 24 và 25 vs
Giúp mk câu 24 và 25 vs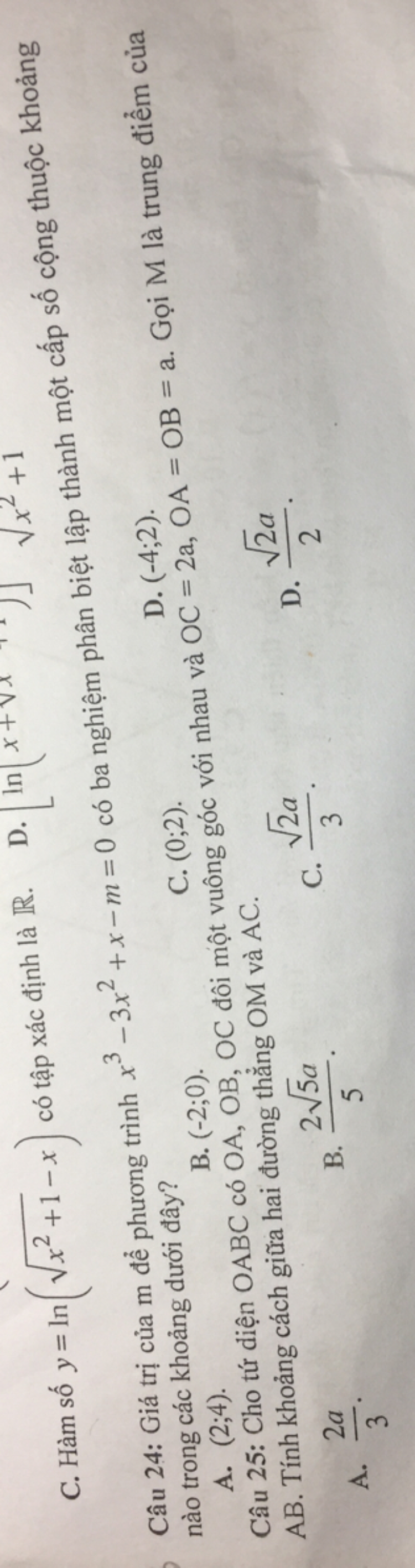 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Khi hàm số |f(x)+m| có 7 điểm cực trị thì pt f(x^3-3x)+m=0 có bao nhiêu nghiệm x thuộc (-2;2)?
bởi Phạm Trúc Vân
 19/01/2020
19/01/2020
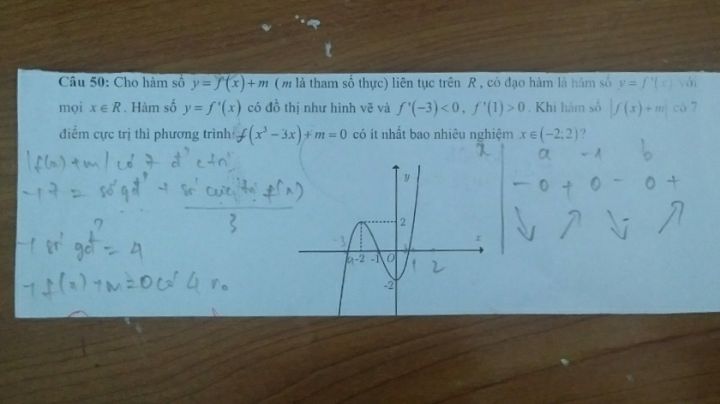 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 1.18 trang 15 SBT Toán 12
Bài tập 1.19 trang 16 SBT Toán 12
Bài tập 1.21 trang 16 SBT Toán 12
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





