Giải bài 1.23 tr 16 SBT Toán 12
Xác định giá trị của tham số m để hàm số \(y = {x^3} - m{x^2} + \left( {m - \frac{2}{3}} \right)x + 5\) có cực trị tại . Khi đó, hàm số đạt cực tiểu hay đạt cực đại ? Tính cực trị tương ứng.
Hướng dẫn giải chi tiết
Ta biết hàm số có cực trị khi phương trình có nghiệm và y’ đổi dấu khi qua các nghiệm đó. Ta có:
\(y' = 3{x^2} - 2mx + \left( {m - \frac{2}{3}} \right)\)
Xét , ta có: \({\rm{\Delta '}} = {m^2} - 3\left( {m - \frac{2}{3}} \right) = {m^2} - 3m + 2\)
khi hoặc (*)
Để hàm số có cực trị tại thì
\(y'\left( 1 \right) = 3 - 2m + m - \frac{2}{3} = 0 \Leftrightarrow m = \frac{7}{3}\) (thỏa mãn điều kiện (*))
Với \(m = \frac{7}{3}\) thì hàm số đã cho trở thành
\({y = {x^3} - \frac{7}{3}{x^2} + \frac{5}{3}x + 5}\)
Ta có
\({y' = 3{x^2} - \frac{{14}}{3}x + \frac{5}{3};\,\,y'' = 6x - \frac{{14}}{3}}\)
Vì \(y''\left( 1 \right) = 6 - \frac{{14}}{3} > 0\) nên hàm số đạt cực tiểu tại và \({y_{CT}} = y\left( 1 \right) = \frac{{16}}{3}\)
-- Mod Toán 12 HỌC247
-

 Ai giải giúp mình bài này với ạ
Ai giải giúp mình bài này với ạ Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm m để hàm số y=x^3-3mx+1 có 2 cực trị B và C cùng với A(2;3) tạo tam giác ABC cân tại A
bởi Nguyễn Thị Thu Hà
 04/07/2019
04/07/2019
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm m để hàm số y=1/3x^3-1/2(3m+2)x^2+(2m^2+3m+1)x-4 có 2 điểm cực trị x=3, x=5
bởi Nguyễn Nhi
 24/06/2019
24/06/2019
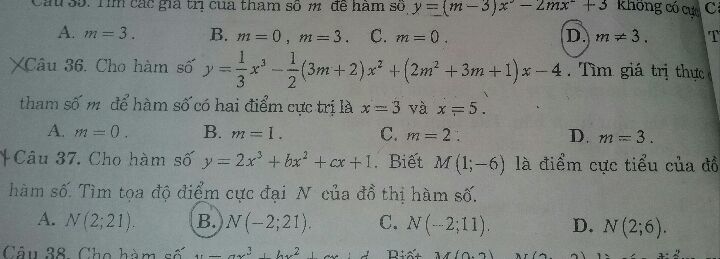 Theo dõi (2) 19 Trả lời
Theo dõi (2) 19 Trả lời -

 Tính khoảng cách giữa 2 điểm cực trị của hàm số y=(x^2 2x) /(x-1)Theo dõi (0) 3 Trả lời
Tính khoảng cách giữa 2 điểm cực trị của hàm số y=(x^2 2x) /(x-1)Theo dõi (0) 3 Trả lời -


Tìm cực trị hàm số y=(7-x). căn bậc 3(x+5)
bởi aladin
 23/06/2019
Giải giúp em câu 10 với ạ
23/06/2019
Giải giúp em câu 10 với ạ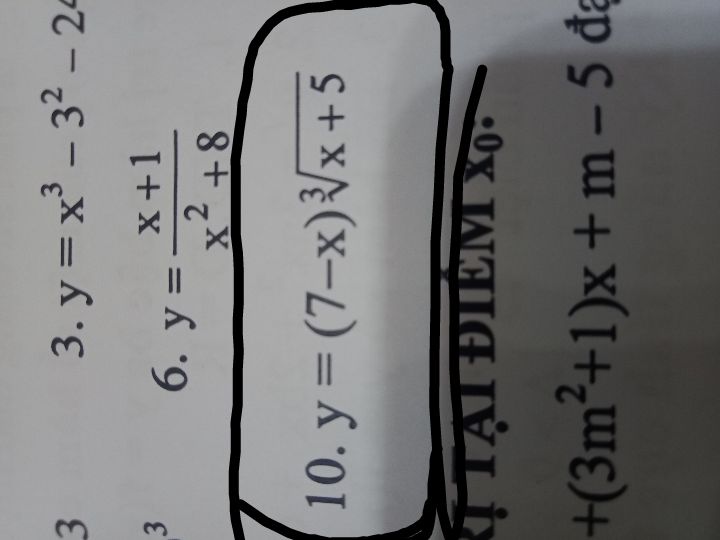 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -

 A.3 B.5 C.2 D.1Theo dõi (0) 9 Trả lời
A.3 B.5 C.2 D.1Theo dõi (0) 9 Trả lời -


Tìm m để hàm số y=1/3x^3-mx^2+(m^2-1)x đạt cực tiểu tại điểm nằm bên phải trục Oy
bởi Ngọc Thoa
 18/06/2019
Giúp mình giải câu này với
18/06/2019
Giúp mình giải câu này với Theo dõi (3) 6 Trả lời
Theo dõi (3) 6 Trả lời -


Tìm tập hợp số thực m để phương trình ln(x^2-mx-2019)=lnx có nghiệm duy nhất
bởi Hữu Nghĩa
 19/05/2019
tập hợp các số thực m để pt ln(x^2-mx-2019)=lnx có nghiệm duy nhất làTheo dõi (0) 0 Trả lời
19/05/2019
tập hợp các số thực m để pt ln(x^2-mx-2019)=lnx có nghiệm duy nhất làTheo dõi (0) 0 Trả lời -


hàm số y=f(x)=(x-1)(x-2)(x-3)...(x-2018) có bao nhiêu điểm cực đại
Theo dõi (1) 9 Trả lời -


Tìm tất cả các giá trị thực để hàm số có 2 điểm cực trị x1, x2 thoả x1^2+x2^2=6
bởi Hồ Minh Nguyệt
 16/12/2018
16/12/2018
Cho hàm số y= x3 -3x2+mx-1.Tìm tất cả các giá trị thực để hàm số có 2 điểm cực trị x1,x2 thoả x12+x22=6
Theo dõi (0) 7 Trả lời -


Số điểm cực trị của hàm số y=(x-1)^2017 ?
bởi Long Phi
 02/12/2018
02/12/2018
Y=(x-1)2017
Theo dõi (0) 5 Trả lời -


Tìm m để (Cm) có ba điểm cực trị A, B, C lập thành một tam giác có bán kính đường tròn
bởi Thụy Thật Thà
 02/12/2018
02/12/2018
Cho hàm số y=x4-2(m+1)x2+1 có đồ thị là (Cm). Tìm m để (Cm) có ba điểm cực trị A, B, C lập thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Theo dõi (0) 5 Trả lời -


Tìm m để pt có 3 nghiệm x căn(9-x)+2m+2=0
bởi Nguyễn Thị hoa
 03/10/2018
03/10/2018
tìm m để pt có 3 nghiệm xcan(9-x)+2m+2=0
b,canx+can(9-x)=can(-x^2+9x+m)
Theo dõi (0) 4 Trả lời -


cho hàm số y=ax^3+bx^2+cx+d , d> 2018, a+b+c+d-2018 <0. Số cực trị của hàm số y= / f(x)-2018/ là
a,3
b,2
c,1
d,5
Theo dõi (1) 1 Trả lời -


Tìm các điểm cực trị của hàm số y =x^2.căn(x^2+2)
bởi Yee Trinh
 30/09/2018
30/09/2018
Tìm các điểm cực trị của hàm số y =x2.
Theo dõi (0) 2 Trả lời -


Tính giá trị biểu thức P=a+3b-3ab biết hàm số y=asin2x+bcos3x-2x đạt cực trị tại x=pi/2
bởi Yee Trinh
 16/09/2018
16/09/2018
Hàm số y=asin2x+bcos3x-2x (0<x<2π) đạt cực trị tại x=π/2 và x=π .Khi đó, giá trị của biểu thức P=a+3b-3ab bằng bao nhiêu ?
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





