Giải bài 1.19 tr 16 SBT Toán 12
Tìm cực trị của các hàm số sau:
a) \(y = x - 6\sqrt[3]{{{x^2}}}\)
b) \(y = \left( {7 - x} \right)\sqrt[3]{{x + 5}}\)
c) \(y = \frac{x}{{\sqrt {10 - {x^2}} }}\)
d) \(y = \frac{{{x^3}}}{{\sqrt {{x^2} - 6} }}\)
Hướng dẫn giải chi tiết
a) TXĐ:
\({y' = 1 - \frac{4}{{\sqrt[3]{x}}} = \frac{{\sqrt[3]{x} - 4}}{{\sqrt[3]{x}}} \Rightarrow y' = 0 \Leftrightarrow x = 64}\)
Bảng biến thiên:
.png)
Vậy ta có \({y_{{\rm{CD}}}} = y\left( 0 \right) = 0;{y_{CT}} = y\left( {64} \right) = - 32\).
b) \(y = \left( {7 - x} \right)\sqrt[3]{{x + 5}}\)
Hàm số xác định trên khoảng
\(y' = - \sqrt[3]{{x + 5}} + \frac{{7 - x}}{{3\sqrt[3]{{{{\left( {x + 5} \right)}^2}}}}} = \frac{{ - 4\left( {x + 2} \right)}}{{3\sqrt[3]{{{{\left( {x + 5} \right)}^2}}}}}\)
Bảng biến thiên:
.png)
Vậy \({y_{{\rm{CD}}}} = y\left( { - 2} \right) = 9\sqrt[3]{3}\)
c) Hàm số xác định trên khoảng \(\left( { - \sqrt {10} ;\sqrt {10} } \right)\)
\(y' = \frac{{\sqrt {10 - {x^2}} + \frac{{{x^2}}}{{\sqrt {10 - {x^2}} }}}}{{10 - {x^2}}} = \frac{{10}}{{\left( {10 - {x^2}} \right)\sqrt {10 - {x^2}} }}\)
Vì với mọi \(x \in \left( { - \sqrt {10} ;\sqrt {10} } \right)\) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
d) Tập xác định: \(D = \left( { - \infty ; - \sqrt 6 } \right) \cup \left( {\sqrt 6 ; + \infty } \right)\).
\(y' = \frac{{3{x^2}\sqrt {{x^2} - 6} - \frac{{{x^4}}}{{\sqrt {{x^2} - 6} }}}}{{{x^2} - 6}} = \frac{{3{x^2}\left( {{x^2} - 6} \right) - {x^4}}}{{\sqrt {{{\left( {{x^2} - 6} \right)}^3}} }} \)
\(= \frac{{2{x^2}\left( {{x^2} - 9} \right)}}{{\sqrt {{{\left( {{x^2} - 6} \right)}^3}} }}\)
Bảng biến thiên:
.jpg)
Từ đó ta thấy hàm số đạt cực đại tại , đạt cực tiểu tại và \({y_{CT}} = y\left( 3 \right) = 9\sqrt 3 ;\)
\({y_{{\rm{CD}}}} = y\left( { - 3} \right) = - 9\sqrt 3 \)
-- Mod Toán 12 HỌC247
-


Tìm cực trị của hs y = -4x^4 - 15x^2 + 7?
bởi Minh Anh
 12/08/2020
Giúp tôi nhaaaaTheo dõi (0) 1 Trả lời
12/08/2020
Giúp tôi nhaaaaTheo dõi (0) 1 Trả lời -


Câu 3: Chọn mệnh đề đúng?
bởi Nguyễn Mỹ Ngọc
 30/07/2020
30/07/2020
 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm cực trị của hàm số y=x 1/x²-2x?
bởi ngọc lan
 26/07/2020
26/07/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Cho hàm số f(x) liên tục trên đoạn [-1;3] và có đồ thị như hình bên.số nghiệm phương trình |f(x)| =1 trên đoạn [-1;3] bằngTheo dõi (0) 0 Trả lời
Cho hàm số f(x) liên tục trên đoạn [-1;3] và có đồ thị như hình bên.số nghiệm phương trình |f(x)| =1 trên đoạn [-1;3] bằngTheo dõi (0) 0 Trả lời -


Số điểm của trị của hàm số g(x) là?
bởi Nguyễn Đức
 20/07/2020
20/07/2020
Giúp em với
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chọn đáp án đúng?
bởi Le Thu Thao
 01/07/2020
Chỉ câu 65,64 giúp mk nhé
01/07/2020
Chỉ câu 65,64 giúp mk nhé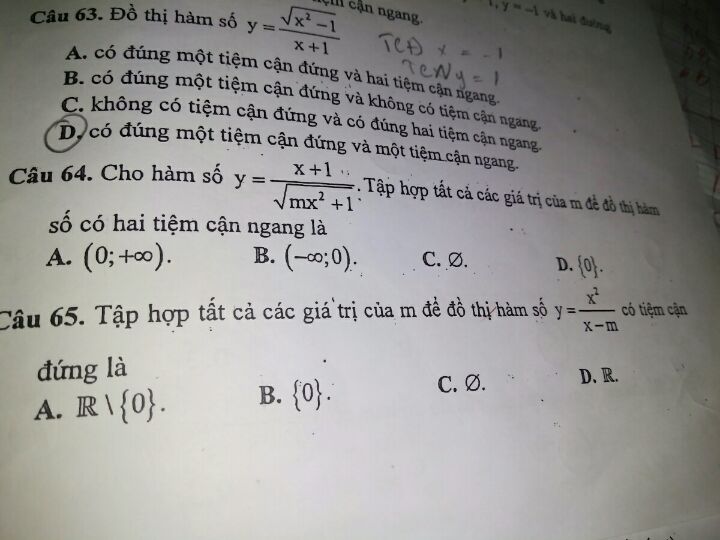 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Chỉ tui điii
Chỉ tui điii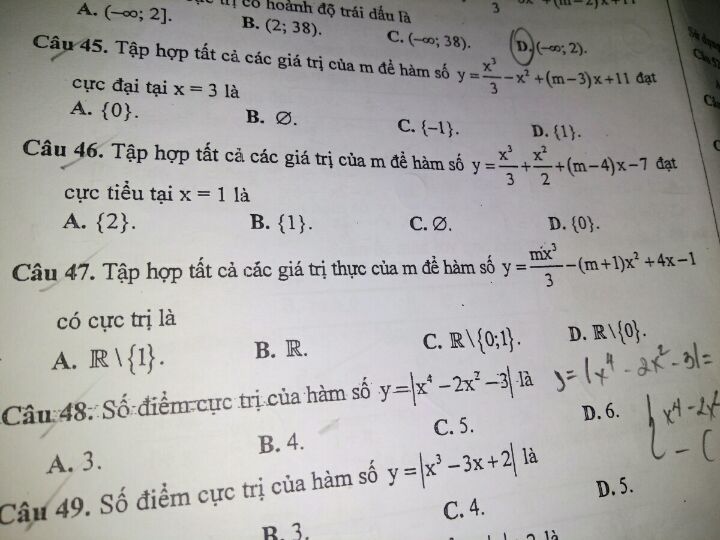 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Phát biểu nao sau đây đúng?
bởi Le Thu Thao
 30/06/2020
30/06/2020
Câu 31 b phai không các bạn?
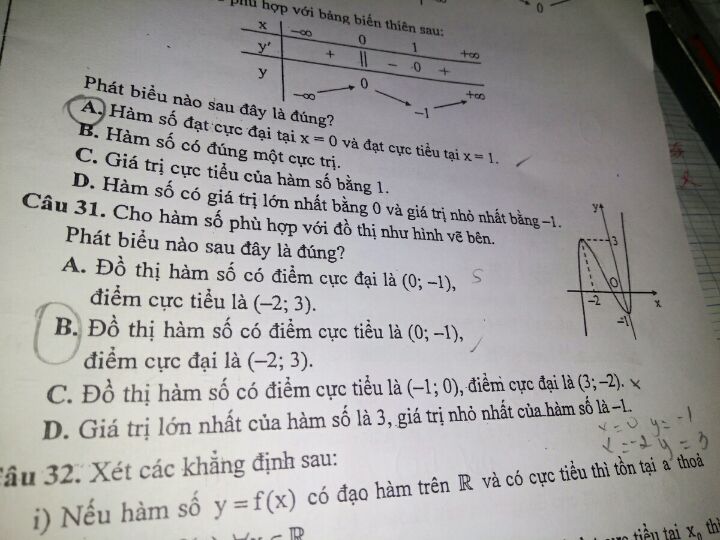 Theo dõi (1) 10 Trả lời
Theo dõi (1) 10 Trả lời -


Chọn đáp án đúng:
bởi Le Thu Thao
 30/06/2020
30/06/2020
Chỉ câu 23,24,25
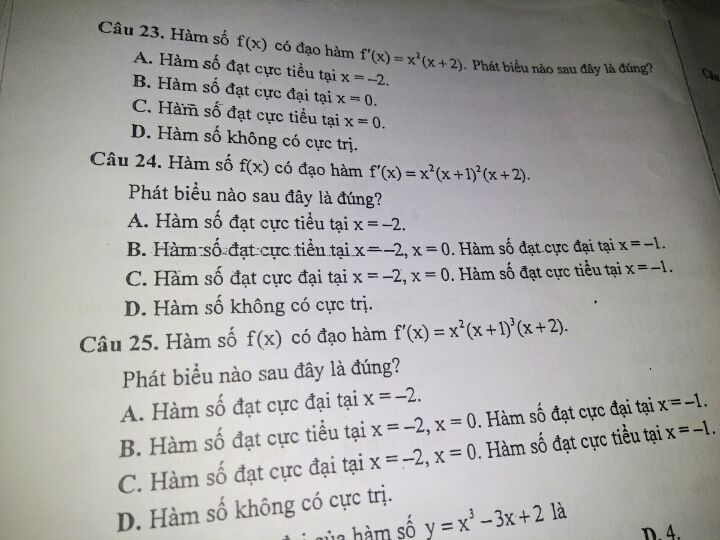 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


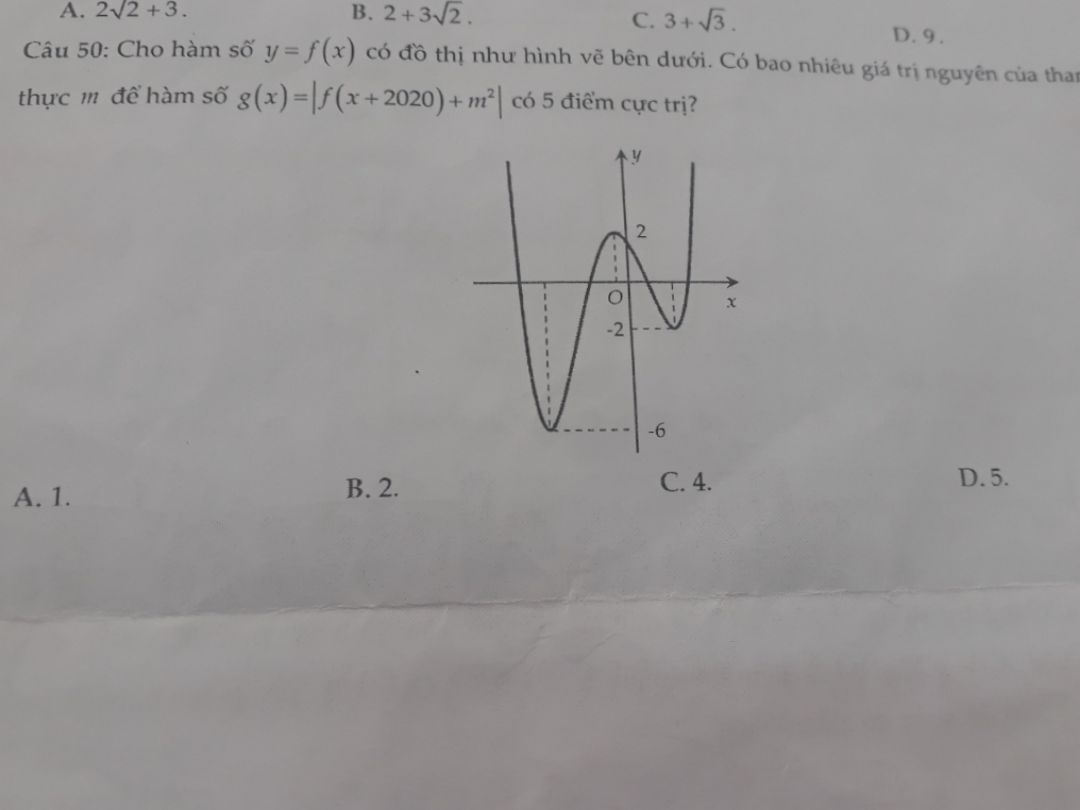 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm a để phương trình 4x^3-3x-4a^3 +3a=0 có hai nghiệm âm và một nghiệm dương?
bởi Ngọc Như
 19/06/2020
19/06/2020
Cho hàm số y=-4x^3 +3x+ 2, có đồ thị là (C). Tìm a để phương trình 4x^3-3x-4a^3 +3a=0 có hai nghiệm âm và một nghiệm dương
Theo dõi (0) 0 Trả lời -


Hàm số \(g(x) = f\left( {{e^x} - \frac{{{x^2} + 2x}}{2}} \right)\) có bao nhiêu điểm cực trị?
bởi Nguyễn thị thúy hằng
 13/06/2020
13/06/2020
Giúp mình câu 46 với ạ
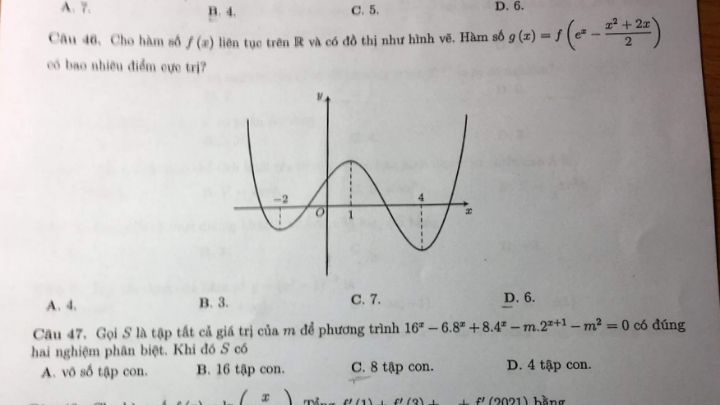 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Số nghiệm thuộc đoạn \(\left[ {0;\frac{{9\pi }}{2}} \right]\) của phương trình?
bởi Nguyễn Lê Ngọc Ánh
 03/06/2020
03/06/2020
Câu 47
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Độ dài đoạn MN bằng?
bởi Thời Tit
 03/06/2020
03/06/2020
..
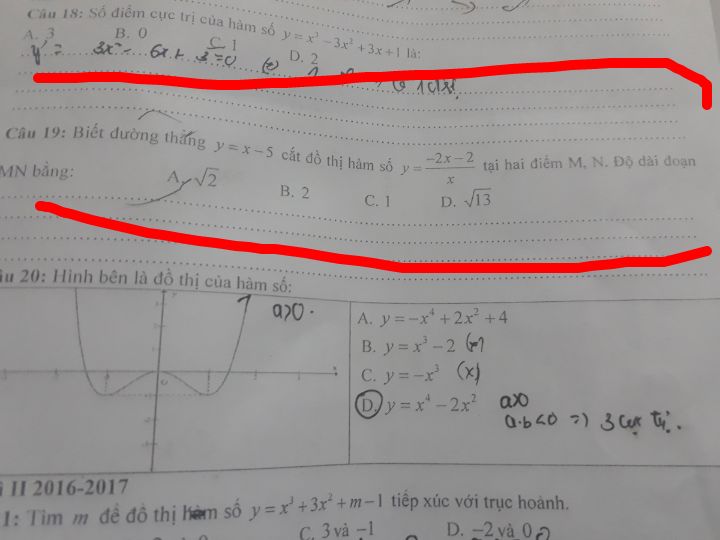 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Đạo hàm có hàm f'(1) bằng?
bởi Bùi Thị Lan Anh
 01/06/2020
01/06/2020
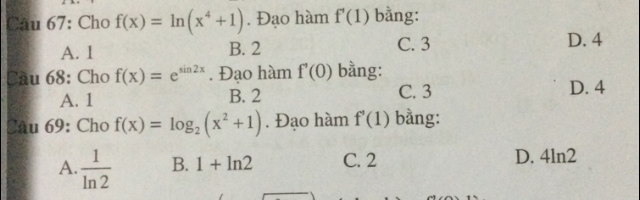 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Định m để hàm số: \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - m + 1} \right)x + 1\) đạt cực tiểu tại x = 1
bởi Nguyễn Sơn Ca
 19/05/2020
19/05/2020
em đang cần gấp, mn giúp em với
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.17 trang 15 SBT Toán 12
Bài tập 1.18 trang 15 SBT Toán 12
Bài tập 1.20 trang 16 SBT Toán 12
Bài tập 1.21 trang 16 SBT Toán 12
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





