Giải bài 1.22 tr 16 SBT Toán 12
Xác định giá trị của tham số m để hàm số \({y = {x^2} - 2{x^2} + mx + 1}\) đạt cực tiểu tại .
Hướng dẫn giải chi tiết
Tập xác định:
\(\begin{array}{l}
y' = 3{x^2} - 4x + m\\
y' = 0 \Leftrightarrow 3{x^2} - 4x + m = 0
\end{array}\)
Phương trình trên có hai nghiệm phân biệt khi
\({\rm{\Delta '}} = 4 - 3m > 0 \Leftrightarrow m < \frac{4}{3}\) (*)
Hàm số có cực trị tại thì
\(y'\left( 1 \right) = 3 - 4 + m = 0 \Rightarrow m = 1\) (thỏa mãn điều kiện (*))
Mặt khác, \(y'' = 6x - 4 \Rightarrow y''(1) = 6 - 4 = 2 > 0\) nên tại , hàm số đạt cực tiểu.
Vậy, với hàm số đã cho có cực tiểu tại .
-- Mod Toán 12 HỌC247
-


Tính diện tích của tam giác OAB biết đồ thị hàm số y=-x^3+3x^2+5 có 2 điểm cực trị A, B
bởi Cao Thị Thu Hiền
 10/12/2019
10/12/2019
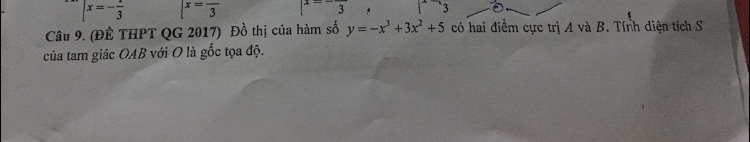 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm m để hàm số đạt cực tiểu tại x=1
bởi Yv Yv
 08/12/2019
08/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tập xác định D của hàm số y=(x−1)^13
bởi Nguyễn Thanh
 08/12/2019
Tìm tập xác định D của hàm số y=(x−1)13.y=(x−1)13.Theo dõi (0) 0 Trả lời
08/12/2019
Tìm tập xác định D của hàm số y=(x−1)13.y=(x−1)13.Theo dõi (0) 0 Trả lời -


Đường cong trong hình vẽ trên dưới là đô thị của hàm số nào dưới đây?
bởi Mai'anh Mai'anh
 06/12/2019
06/12/2019
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Câu 26 ạ
Câu 26 ạ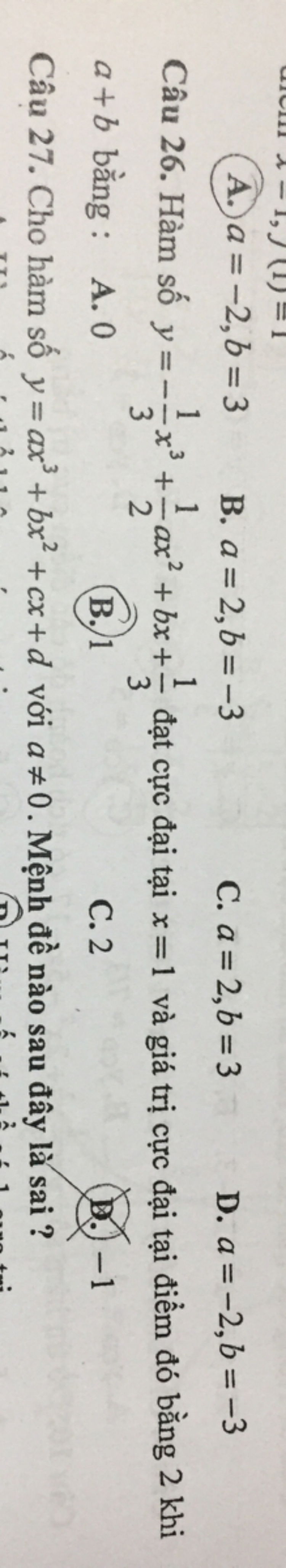 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm cực trị của hàm số y=x^4+2x^2-3
bởi Nguyễn ĐạiHiệp
 01/12/2019
01/12/2019
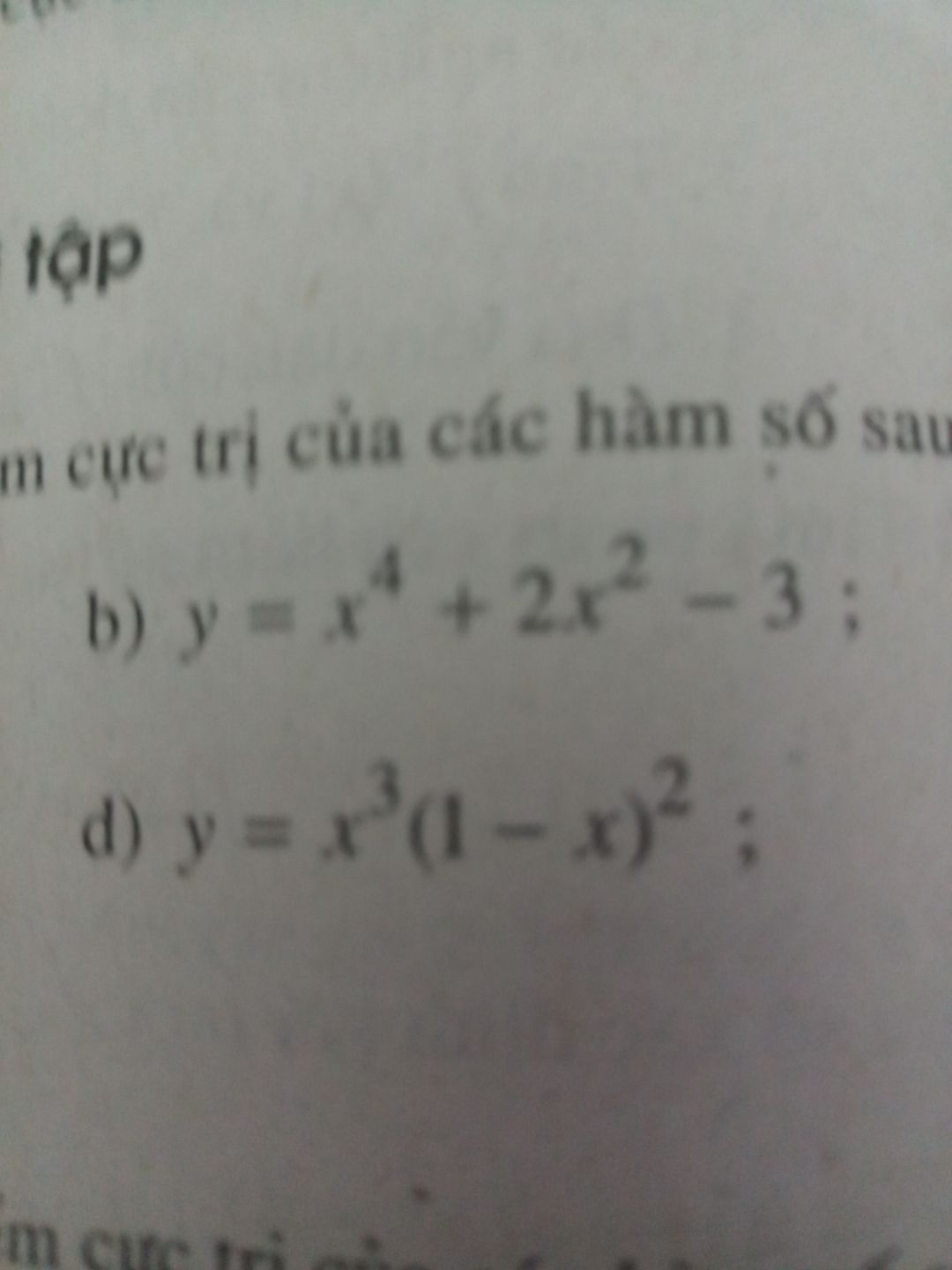 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m đêt đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có diện tích bằng 1
bởi Vu Minh Anh
 24/11/2019
24/11/2019
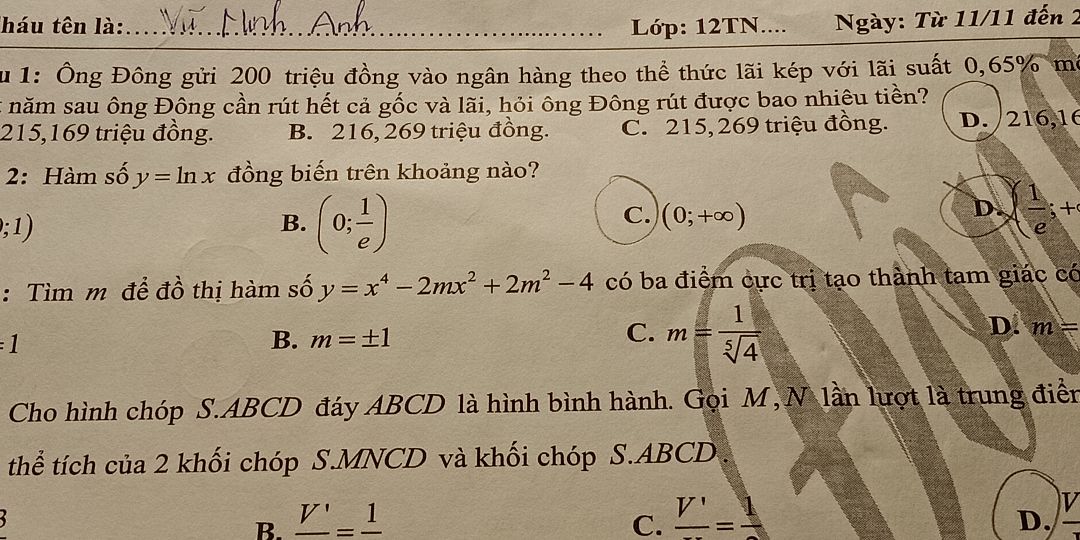 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -

 A. S=9B. S=10/3C. S=10D. S=5Theo dõi (0) 2 Trả lời
A. S=9B. S=10/3C. S=10D. S=5Theo dõi (0) 2 Trả lời -

 Câu 29 làm ntn ạ?
Câu 29 làm ntn ạ? Theo dõi (0) 11 Trả lời
Theo dõi (0) 11 Trả lời -

 Giúp mk với ạ
Giúp mk với ạ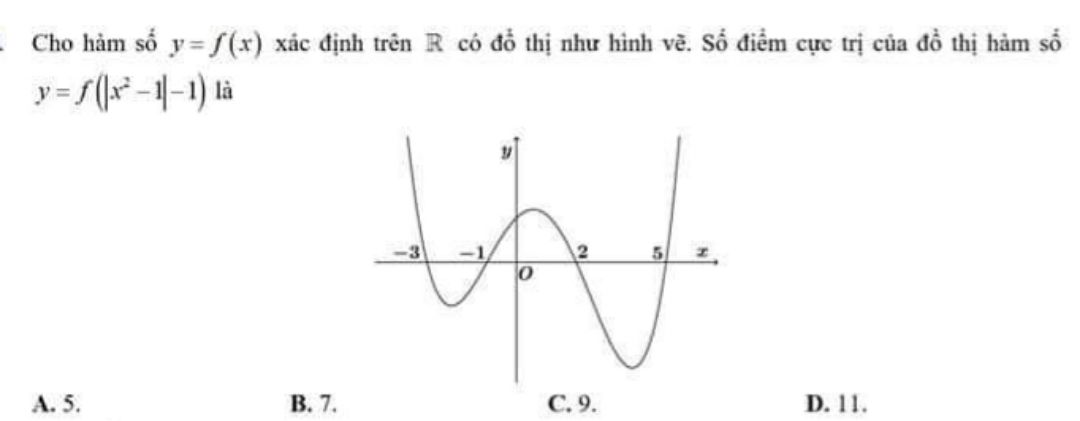 Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Tìm m để đồ thị hàm số y=x^4-2mx^2+2m-3 có 3 điểm cực trị là ba đỉnh của một tam giác cân
bởi Thương Phan
 22/10/2019
Tìm tất cả các giá trị của m để đồ thị hàm số y=x^4-2mx^2 2m-3 có ba điểm cực trị là ba đỉnh của một tam giác cânTheo dõi (0) 7 Trả lời
22/10/2019
Tìm tất cả các giá trị của m để đồ thị hàm số y=x^4-2mx^2 2m-3 có ba điểm cực trị là ba đỉnh của một tam giác cânTheo dõi (0) 7 Trả lời -


Tìm số điểm cực trị của f(x) biết f(x) có đạo hàm f'(x)=(x+1)^2(x-2)^3(2x+3)
bởi Trúc Thanh
 19/10/2019
19/10/2019
 Theo dõi (0) 11 Trả lời
Theo dõi (0) 11 Trả lời -


Tìm m để đồ thị hàm số y=mx^4+(2m-1)x^2+m-2 chỉ có cực đại mà không có cực tiểu
bởi Quốc Lực Phan
 19/10/2019
19/10/2019
 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Biện luận số nghiệm của phương trình x^4-4x^2-2m=0?
bởi Ngoan Ngọc
 16/10/2019
Biện luận số nghiệm của phương trình x^4-4x^2-2m=0Theo dõi (0) 6 Trả lời
16/10/2019
Biện luận số nghiệm của phương trình x^4-4x^2-2m=0Theo dõi (0) 6 Trả lời -


Có tất cả bao nhiêu giá trị nguyên của m để hàm số y=mx^4+(2m-5)x^2+m+1 có 3 cực trị?
bởi Phạm Trang
 14/10/2019
Câu 26
14/10/2019
Câu 26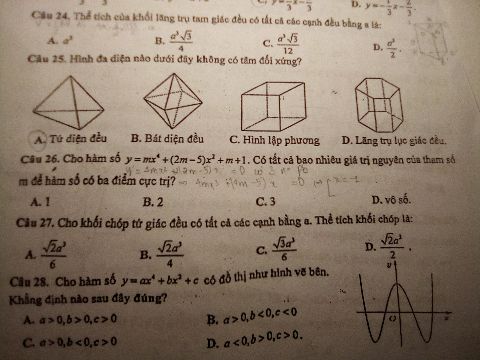 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời
Bài tập SGK khác
Bài tập 1.20 trang 16 SBT Toán 12
Bài tập 1.21 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





