Giải bài 1.24 tr 16 SBT Toán 12
Chứng minh rằng hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
- 2x,\,\,\,\,x \ge 0\\
\sin \frac{x}{2},\,\,x < 0
\end{array} \right.\)
không có đạo hàm tại nhưng đạt cực đại tại điểm đó.
Hướng dẫn giải chi tiết
Hàm số
\(f\left( x \right) = \left\{ \begin{array}{l}
- 2x,\,\,\,\,x \ge 0\\
\sin \frac{x}{2},\,\,x < 0
\end{array} \right.\)
Không có đạo hàm tại vì:
\(\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{ - 2x}}{x} = - 2,}\\
\begin{array}{l}
\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin \frac{x}{2}}}{x}\\
= \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin \frac{x}{2}}}{{2.\frac{x}{2}}} = \frac{1}{2}
\end{array}
\end{array}\)
Mặt khác, với thì \(y' = \frac{1}{2}\cos \frac{x}{2}\), với thì
Bảng biến thiên
.png)
Từ đó, ta thấy hàm số đạt cực đại tại và
-- Mod Toán 12 HỌC247
-

 Cho hàm số y=x^4-2mx^2 2m-m^4 .Tìm m để ba cực trị của hàm số tạo thành tam giác đều
Cho hàm số y=x^4-2mx^2 2m-m^4 .Tìm m để ba cực trị của hàm số tạo thành tam giác đều Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Hàm số y=x^4+3x^2-4 có bao nhiêu điểm cực trị?
bởi Trung Nghĩa
 10/10/2019
10/10/2019
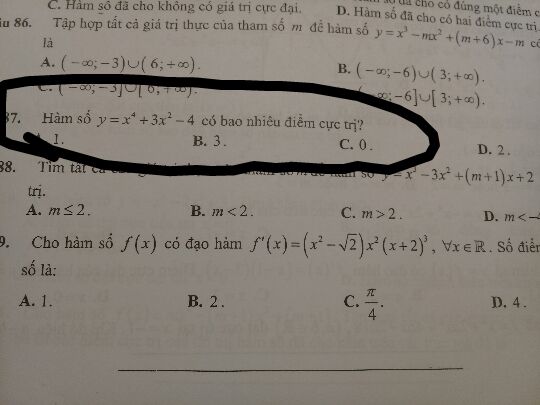 Theo dõi (0) 11 Trả lời
Theo dõi (0) 11 Trả lời -


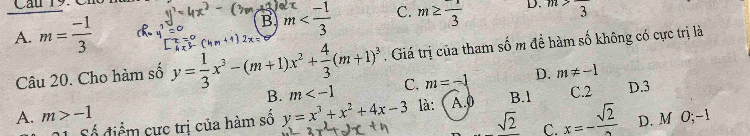 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -

 Tìm m
Tìm m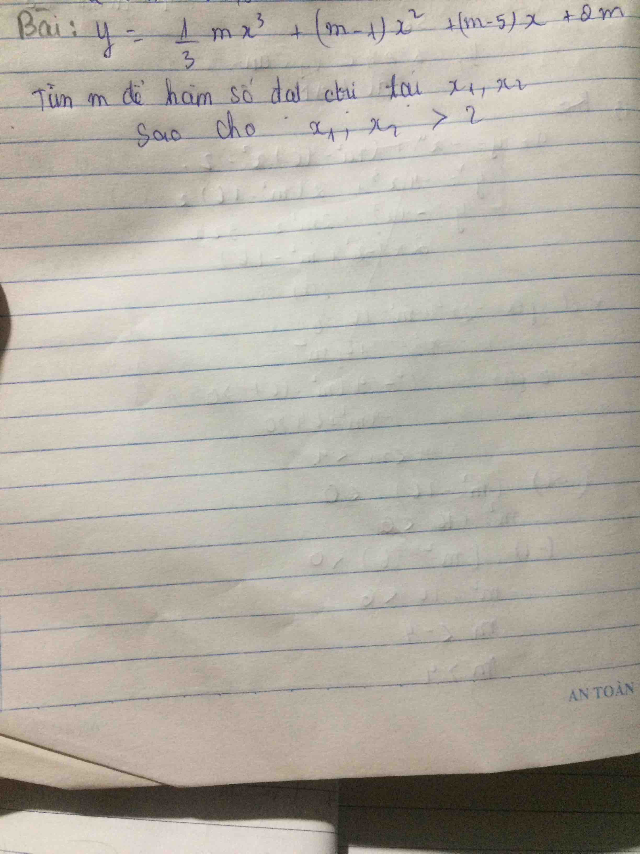 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 Tìm m
Tìm m Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm m để đồ thị hàm số y=x^4-2mx^2 có ba điểm cực trị tạo thành 1 tam giác có diện tích nhỏ hơn 1
bởi Trần Hữu Hoàng
 06/10/2019
06/10/2019
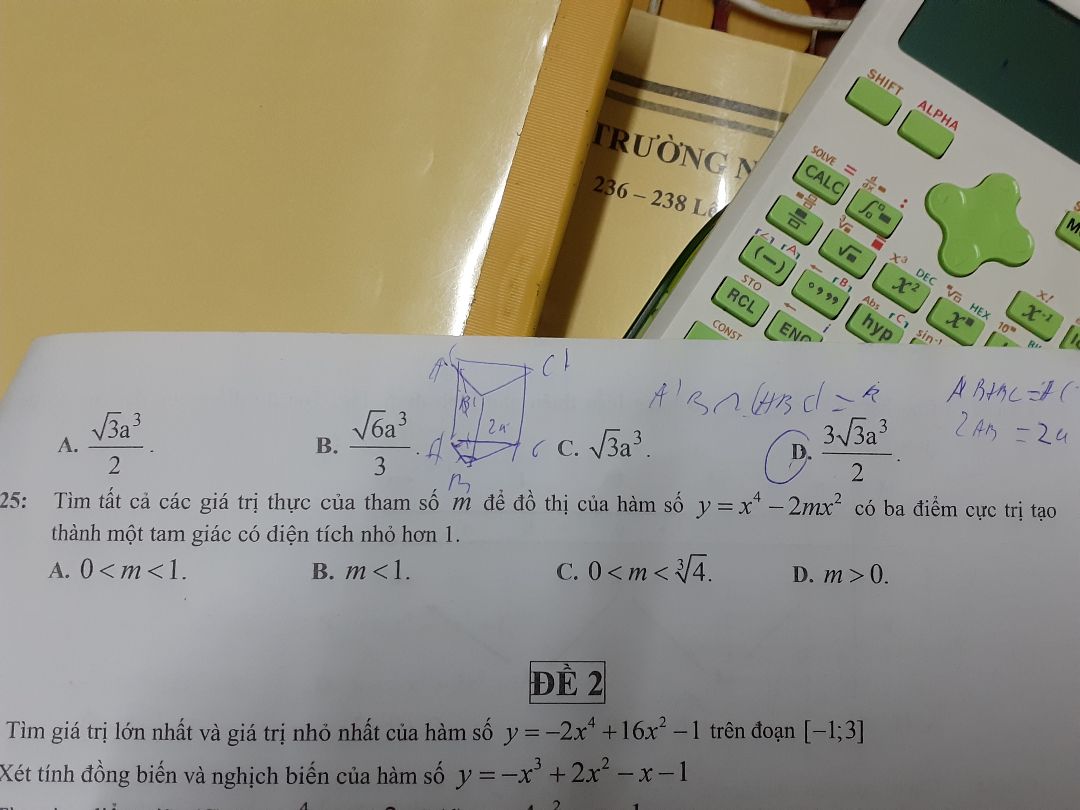 Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -

 Làm sao
Làm sao Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tìm số cực trị của hàm số y=1/x
bởi Nguyễn Văn Đoàn
 27/09/2019
27/09/2019
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tìm cực trị hàm số y= căn (1-2x+x^2)
bởi le dinh phong
 09/09/2019
09/09/2019
y= căn (1-2x+x^2)
y= trị tuyệt đối của x^2-4x+1
Theo dõi (2) 5 Trả lời -


Viết pt đt ∆ đi qua 2 đ.cực trị của y= x^3/3 - x^2 - 2x
bởi nguyen
 26/08/2019
Viết pt đt ∆ đi qua 2 đ.cực trị của y= x^3/3 - x^2 - 2xTheo dõi (0) 4 Trả lời
26/08/2019
Viết pt đt ∆ đi qua 2 đ.cực trị của y= x^3/3 - x^2 - 2xTheo dõi (0) 4 Trả lời -

 Giá trị m để hàm số f(x) = 1/3x^3 -mx^2 (4m-3)x 1 đạt cực đại, cực tiểu
Giá trị m để hàm số f(x) = 1/3x^3 -mx^2 (4m-3)x 1 đạt cực đại, cực tiểu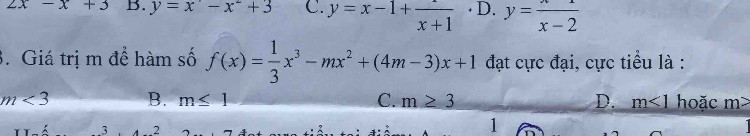 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm m để hàm số y=m/3x^3-(m-1)x^2+3(m-2)x+1 đạt cực trị tại x1, x2 thỏa x1+2x2=1
bởi Đỗ Hà Chi
 31/07/2019
31/07/2019
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm m để đồ thị hàm số y=x^4-2mx^2+2 có 3 điểm cực trị A, B, C thỏa OA.OB.OC=12
bởi Nguyễn Nhi
 24/07/2019
24/07/2019
 Theo dõi (2) 6 Trả lời
Theo dõi (2) 6 Trả lời -


cho hàm số
.để hàm số đạt cực đại x1;x2 Tm X1+2X2=1 thì giá trị cần tìm của m là bao nhiêu ?? giúp e với e vám ơn ạ
Theo dõi (1) 6 Trả lời -


Tìm m để hàm số y=x^3=2(m-1)X^2+(m^2-4m+1)x-2 có cực đại, cực tiểu tại x1, x2
bởi Thu Thủy
 08/07/2019
08/07/2019
Xác định giá trị của m để hàm số y=X^3=2(m-1)X^2+(m^2-4m+1)x-2 có cực đại , cực tiểu tại X1,X2 thỏa mãn 1/X1 +1/X2 = X1+X2/2
Theo dõi (0) 2 Trả lời -


Tính tỉ số MP/NP biết (d) là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
bởi Anh Pham
 08/07/2019
08/07/2019
Cho hàm số y = x^3 - 3x^2 + 4 và M(3;2), N(-1;0). Gọi (d) là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đường thẳng (MN) cắt (d) tại P. Tính tỉ số MP/NP
Theo dõi (0) 5 Trả lời
Bài tập SGK khác
Bài tập 1.21 trang 16 SBT Toán 12
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





