Giải bài 1.18 tr 15 SBT Toán 12
Tìm cực trị của các hàm số sau:
a) \(y = \frac{{x + 1}}{{{x^2} + 8}}\)
b) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\)
c) \(y = \frac{{{x^2} + x - 5}}{{x + 1}}\)
d) \(y = \frac{{{{(x - 4)}^2}}}{{{x^2} - 2x + 5}}\,\)
Hướng dẫn giải chi tiết
a) TXĐ:
\(\begin{array}{l}
y' = \frac{{{x^2} + 8 - 2x\left( {x + 1} \right)}}{{{{\left( {{x^2} + 8} \right)}^2}}} = \frac{{ - {x^2} - 2x + 8}}{{{{\left( {{x^2} + 8} \right)}^2}}}\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 4\\
x = 2
\end{array} \right.
\end{array}\)
Bảng biến thiên:
.png)
Hàm số đạt cực đại tại , cực tiểu tại và \({y_{{\rm{CD}}}} = y\left( 2 \right) = \frac{1}{4};\)
\({y_{CT}} = y\left( { - 4} \right) = - \frac{1}{8}\).
b) Hàm số xác định và có đạo hàm với mọi
\({y' = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}} \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1 - \sqrt 2 \\
x = 1 + \sqrt 2
\end{array} \right.}\)
Bảng biến thiên:
.png)
Hàm số đạt cực đại tại \(x = 1 - \sqrt 2 \), đạt cực tiểu tại \(x = 1 + \sqrt 2 \)
Ta có: \({y_{{\rm{CD}}}} = y\left( {1 - \sqrt 2 } \right) = - 2\sqrt 2 ;\)
\({y_{CT}} = y\left( {1 + \sqrt 2 } \right) = 2\sqrt 2 \).
c) TXĐ:
\(y' = \frac{{{x^2} + 2x + 6}}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \ne - 1\)
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
d) \(y = \frac{{{{\left( {x - 4} \right)}^2}}}{{{x^2} - 2x + 5}}\)
Vì \({x^2} - 2x + 5\) luôn dương nên hàm số xác định trên .
\(y' = \frac{{2\left( {x - 4} \right)\left( {{x^2} - 2x + 5} \right) - {{\left( {x - 4} \right)}^2}\left( {2x - 2} \right)}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}\)
\( = \frac{{2\left( {x - 4} \right)\left( {3x + 1} \right)}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = - \frac{1}{3}}\\
{x = 4}
\end{array}} \right.\)
Bảng biến thiên:
.png)
Hàm số đạt cực đại tại \(x = - \frac{1}{3}\), đạt cực tiểu tại và \({y_{{\rm{CD}}}} = y\left( { - \frac{1}{3}} \right) = \frac{{13}}{4};\)
\({y_{CT}} = y\left( 4 \right) = 0\).
-- Mod Toán 12 HỌC247
-


Cho hàm số có đạo hàm f'(x)=(4-x)(x^3-1)+2x số điểm cực trị của f(x^{2})-x^{4}-m
bởi Ng Dung
 21/01/2021
21/01/2021
cho hàm số có đạo hàm f'(x)=(4-x)(x^3-1)+2x số điểm cực trị của f(x^{2})-x^{4}-m
Theo dõi (1) 3 Trả lời -

 Câu 25 ạ
Câu 25 ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Xét tính đơn điệu của hàm số:
y = sin^2(x) + cos(x) với x thuộc [0;pi]
Theo dõi (0) 0 Trả lời -


Tìm m để hàm số (y = m{x^4} + (2m - 1){x^3} + m - 2) chỉ có cực đại và không có cực tiểu.
bởi Hoàng Minh Phúc
 08/09/2020
08/09/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Hàm số f(x)=x^2-2|x| 2016 có bao nhiêu cực trị?
bởi Híp
 31/08/2020
Số cực trị của hàm số f(x)=x^2-2|x| 2016 là???Theo dõi (0) 4 Trả lời
31/08/2020
Số cực trị của hàm số f(x)=x^2-2|x| 2016 là???Theo dõi (0) 4 Trả lời -


Có bao nhiêu số nguyên m để hàm số có 2 điểm cực trị đồng thời giá trị cực trị cùng dấu?
bởi Nguyễn Tiến Dũng
 28/08/2020
Câu 5 ạ
28/08/2020
Câu 5 ạ Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm m đê hàm số có cực đại, cực tiểu?
bởi Thanh Vân
 26/08/2020
26/08/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


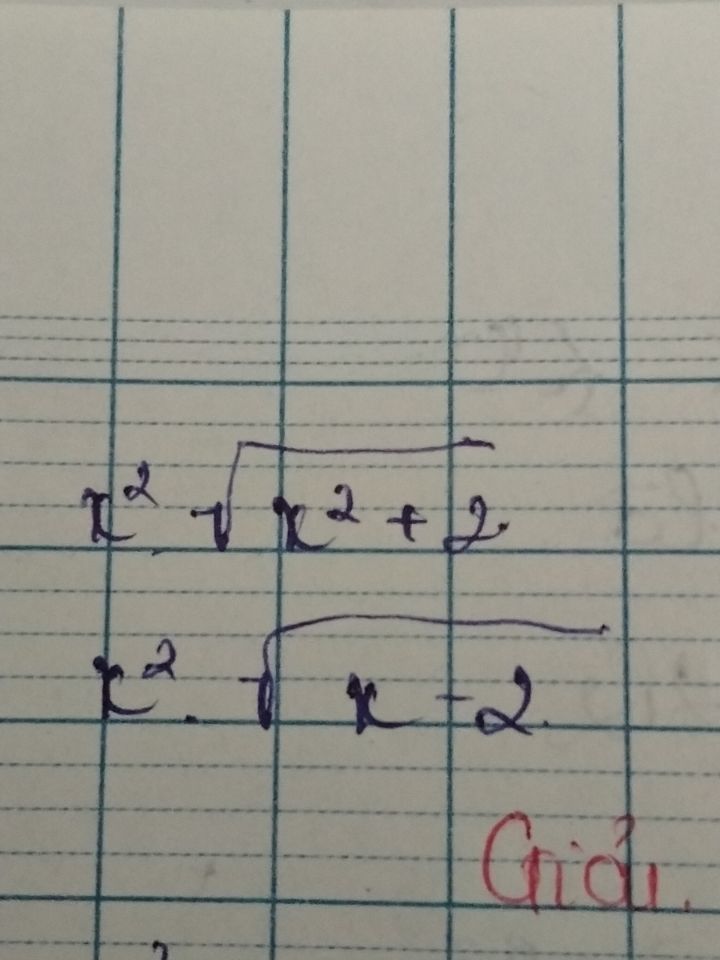
Tính đạo hàm của \(x^2.\sqrt {x^2+2}\)?
bởi Đặng Thùy Linh
 25/08/2020
25/08/2020
giúp mình tìm đạo hàm câu này với
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giá trị m để đồ thị hàm số có 2 điểm cực trị nằm về 2 phía của trục Ox?
bởi Hương Lê Thị Diễm
 24/08/2020
24/08/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Ý d ạ
Ý d ạ Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Trung điểm của đoạn thẳng nối 2 điểm cực trị của đồ thị hàm số \(y=(x-1)(x-2)^2\) nằm trên đường thẳng nào?
bởi Hà Nguyễn
 20/08/2020
20/08/2020
Cho hàm số y=(x-1)(x-2)^2 .Trung điểm của đoạn thẳng nối 2 điểm cực trị của đồ thị hàm số nằm trên đường thẳng nào?
Theo dõi (1) 1 Trả lời -


Giúp mình câu 9 với!
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Xác định dấu cực trị của hàm số f'(x) biết \(f(x)=(x^4-1)(4-2x)^3.x^9\)?
bởi Đặng Linh
 18/08/2020
18/08/2020
Xác định dấu cực trị của hàm số f'(x) biết
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Có bao nhiêu giá trị nguyên m thỏa mãn bài toán?
bởi Kim Hoa
 12/08/2020
12/08/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm cực trị của hs \(y =\dfrac{ -2x + 3}{ x+ 1}\)?
bởi Minh Anh
 12/08/2020
12/08/2020
Giúp tôi nha
Theo dõi (0) 3 Trả lời -


Tìm cực trị của hs \(y = x^3 + 3x^2 + 10x - 6\)?
bởi Minh Anh
 12/08/2020
12/08/2020
Giải chi tiết hộ tôi nha
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 6 trang 18 SGK Giải tích 12
Bài tập 1.17 trang 15 SBT Toán 12
Bài tập 1.19 trang 16 SBT Toán 12
Bài tập 1.20 trang 16 SBT Toán 12
Bài tập 1.21 trang 16 SBT Toán 12
Bài tập 1.22 trang 16 SBT Toán 12
Bài tập 1.24 trang 16 SBT Toán 12
Bài tập 1.23 trang 16 SBT Toán 12
Bài tập 1.25 trang 16 SBT Toán 12
Bài tập 1.26 trang 16 SBT Toán 12
Bài tập 1.27 trang 17 SBT Toán 12
Bài tập 1.28 trang 17 SBT Toán 12
Bài tập 1.29 trang 17 SBT Toán 12
Bài tập 1.30 trang 17 SBT Toán 12
Bài tập 1.31 trang 17 SBT Toán 12
Bài tập 1.32 trang 17 SBT Toán 12
Bài tập 1.33 trang 17 SBT Toán 12
Bài tập 11 trang 16 SGK Toán 12 NC
Bài tập 12 trang 17 SGK Toán 12 NC
Bài tập 13 trang 17 SGK Toán 12 NC





