Bài tập 4 trang 121 SGK Hình học 11

69 BT SGK

Giải bài 4 tr 121 sách GK Toán Hình lớp 11

Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc \(\widehat{BAD} = 60^o\). Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và \(SO = \frac{3a}{4}\). Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.

a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).

b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).

Hướng dẫn giải chi tiết bài 4

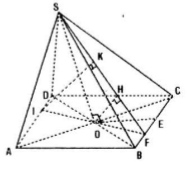
Câu a:

Vì E là trung điểm BC và O là trung điểm AC.

\(\Rightarrow OE=\frac{1}{2}AB=\frac{a}{2}\)

Do ABCD là hình thoi nên góc \(\widehat {BAD} = {60^0}.\)

\(\Rightarrow \Delta BAD\) đều \(\Rightarrow BD=a\Rightarrow OB=\frac{a}{2}\)

\(\Rightarrow \Delta OBE\) làm tam giác đều.

F là trung điểm \(BE\Rightarrow OF\perp BE\Rightarrow OF\perp BC\) (1)

Lại có \(SO \perp (ABCD)\Rightarrow SO\perp BC\) (2)

Từ (1) và (2) suy ra \(BC\perp (SOF)\)

Mà \(BC\subset (SBC)\Rightarrow (SOF )\perp (SBC)\) (đpcm).

Câu b:

Trong mặt phẳng (SOF) và \(OH\perp SF(H\in SF)\)

vì \(BC\perp (SOF)\Rightarrow BC\perp OH\Rightarrow OH\perp (SBC)\)

⇒ độ dài đoạn thẳng OH là khoảng cách từ O đến mặt phẳng (SBC).

Trong tam giác vuông OSF có đường cao \(OH\Rightarrow \frac{1}{OH^2}=\frac{1}{OS^2}+\frac{1}{OF^2}\)

\(\Rightarrow \frac{1}{OH^2} = \frac{1}{\frac{9a^2}{16}}+\frac{1}{\frac{3a^2}{16}}= \frac{64}{9a^2}\Rightarrow OH=\frac{3a}{8}\)

Gọi I là giao điểm của OF và AD. Trong mặt phẳng (SIF) dựng \(IK\perp SF\)

Vì \(OH\perp SF, IK\perp SF\Rightarrow OH // IK\Rightarrow IK\perp (SBC)\)

⇒ độ dài đoạn thẳng IK là khoảng cách từ I đến mặt phẳng (SBC)

Lại thấy \(I\in AD\) mà AD // (SBC) ⇒ IK là khoảng csch từ AD đến mặt phẳng (SBC) hay IK là khoảng cách từ A đến mặt phẳng (SBC).

Dễ thấy OH là đường trung bình của \(\Delta FIK\)

\(\Rightarrow IK=3.OH=\frac{3a}{4}\)

Vậy \(d(O,(SBC))=\frac{3a}{8}\) và \(d(A,(SBC))=\frac{3a}{4}\).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 4 trang 121 SGK Hình học 11 HAY thì click chia sẻ

YOMEDIA

Trong không gian cho điểm \(O\) và bốn điểm \(A, B, C, D\) không thẳng hàng. Điều kiện cần và đủ để \(A, B, C, D\) tạo thành hình bình hành là:

bởi Lan Anh 26/02/2021

A. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).

B. \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \).

C. \(\overrightarrow {OA} + \dfrac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \dfrac{1}{2}\overrightarrow {OD} \).

D. \(\overrightarrow {OA} + \dfrac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \dfrac{1}{2}\overrightarrow {OD} \).

Theo dõi (0) 1 Trả lời
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Chọn khẳng định sai ?

bởi Hoang Viet 25/02/2021

A. \(\overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {B{B_1}} = \overrightarrow {B{D_1}} \).

B. \(\overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {{B_1}{C_1}} + \overrightarrow {{B_1}{A_1}} \).

C. \(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {DC} \).

D. \(\overrightarrow {BA} + \overrightarrow {D{D_1}} + \overrightarrow {B{D_1}} = \overrightarrow {BC} \).

Theo dõi (0) 1 Trả lời
Cho tứ diện \(ABCD\). Đặt \(\overrightarrow {AB} = \overrightarrow b \,,\,\overrightarrow {AC} = \,\overrightarrow c \,,\,\overrightarrow {AD} = \overrightarrow d \). Gọi G là trọng tâm của tam giác BCD. Trong các đẵng thức sau, đẳng thức nào đúng ?

bởi Xuan Xuan 25/02/2021

A. \(\overrightarrow {AG} = \dfrac{1}{4}\left( {\overrightarrow b + \overrightarrow c + \overrightarrow d } \right)\).

B. \(\overrightarrow {AG} = \dfrac{1}{3}\left( {\overrightarrow b + \overrightarrow c + \overrightarrow d } \right)\).

C. \(\overrightarrow {AG} = \dfrac{1}{2}\left( {\overrightarrow b + \overrightarrow c + \overrightarrow d } \right)\).

D. \(\overrightarrow {AG} = \overrightarrow d + \overrightarrow c + \overrightarrow b \).

Theo dõi (0) 1 Trả lời
Cho hai hình vuông \(ABCD\) và \(ABEF\) cạnh a nằm trên hai mặt phẳng vuông góc . Đường thẳng DE vuông góc với:

bởi thuy tien 25/02/2021

A. Chỉ với AC.

B. Chỉ với BF.

C. Chỉ với AC và BF.

D. Hoặc với AC hoặc với BF.

Theo dõi (0) 1 Trả lời