Giải bài 3.51 tr 163 SBT Hình học 11
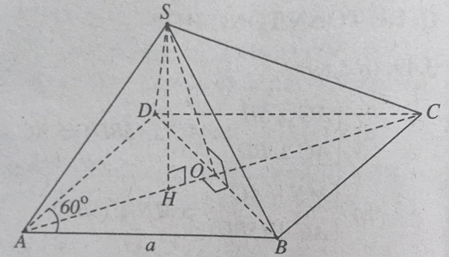
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, \(BAD = {60^0}\), SA = SB = SD = a.
a) Chứng minh (SAC) vuông góc với (ABCD).
b) Chứng minh tam giác SAC vuông.
c) Tính khoảng cách từ S đến (ABCD).
Hướng dẫn giải chi tiết
a) Tam giác ABD là tam giác đều. Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABD), ta có:
SA = SB = SD ⇒ H là tâm đường tròn ngoại tiếp tam giác ABD ⇒ H là trọng tâm tam giác ABD.
Do đó H ∈ AC, suy ra (SAC) ⊥ (ABCD).
b) Ta có:
\(AH = \frac{2}{3}AO = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
\(AH.AC = \frac{{a\sqrt 3 }}{3}.a\sqrt 3 = {a^2} = A{S^2} \Rightarrow \) \(\Delta SAC\) vuông tại S.
c) \(d\left[ {S,\left( {ABCD} \right)} \right] = SH = \sqrt {HA.HC} = \frac{{a\sqrt 6 }}{3}\)
-- Mod Toán 11 HỌC247
-


A. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD} \).
B. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AB'} \).
C. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
D. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD'} \).
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S. ABC\) có đáy là tam giác đều cạnh a, \(SA \bot (ABC)\,,SA = \dfrac{a}{2}\).Từ A kẻ \(AH \bot SM\) với M là trung điểm của của BC. Khi dđó góc giữa hai vec tơ \(\overrightarrow {SA} \,,\overrightarrow {AH} \) bằng:
bởi May May
 25/02/2021
25/02/2021
A. 400
B. 450
C. 900
D. 1500
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh a, \(SA = a\sqrt {3\,} ,\,SA \bot BC\). Tính góc giữa hai đường thẳng \(SD\) và \(BC\) ?
bởi Nhi Nhi
 26/02/2021
26/02/2021
A.900
B. 600
C. 450
D. 300
Theo dõi (0) 1 Trả lời -


Cho hình lập phương \(ABCD.A’B’C’D’\). Hình chiếu vuông góc của A lên mặt phẳng \((A’BD)\) là:
bởi bich thu
 26/02/2021
26/02/2021
A. Trung điểm của BD.
B. Trung điểm của A’B.
C. Trung điểm của A’D.
D. Tâm O của tam giác BDA’.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.49 trang 163 SBT Hình học 11
Bài tập 3.50 trang 163 SBT Hình học 11
Bài tập 3.52 trang 163 SBT Hình học 11
Bài tập 3.53 trang 163 SBT Hình học 11
Bài tập 3.54 trang 164 SBT Hình học 11
Bài tập 3.55 trang 164 SBT Hình học 11
Bài tập 3.56 trang 164 SBT Hình học 11
Bài tập 3.57 trang 164 SBT Hình học 11
Bài tập 3.58 trang 164 SBT Hình học 11
Bài tập 3.59 trang 165 SBT Hình học 11
Bài tập 3.60 trang 165 SBT Hình học 11
Bài tập 3.61 trang 165 SBT Hình học 11
Bài tập 3.62 trang 165 SBT Hình học 11
Bài tập 3.63 trang 165 SBT Hình học 11
Bài tập 3.64 trang 165 SBT Hình học 11
Bài tập 3.65 trang 165 SBT Hình học 11
Bài tập 3.66 trang 166 SBT Hình học 11
Bài tập 3.67 trang 166 SBT Hình học 11
Bài tập 3.68 trang 166 SBT Hình học 10
Bài tập 3.69 trang 166 SBT Hình học 11
Bài tập 3.70 trang 167 SBT Hình học 11
Bài tập 3.71 trang 167 SBT Hình học 11
Bài tập 3.72 trang 167 SBT Hình học 11
Bài tập 3.73 trang 168 SBT Hình học 11
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC