Bài tập 3.50 trang 163 SBT Hình học 11

Lý thuyết10 Trắc nghiệm

69 BT SGK

238 FAQ

Giải bài 3.50 tr 163 SBT Hình học 11

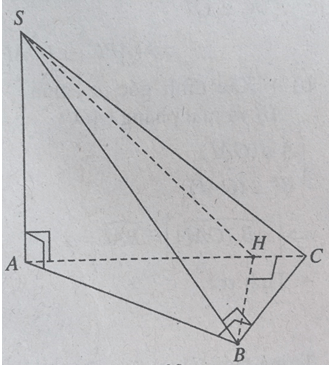
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.

a) Chứng minh tam giác SBC vuông

b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.

Chứng minh (SAC) ⊥ (SBH)

c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)

Hướng dẫn giải chi tiết

Giải sách bài tập Toán 11 | Giải sbt Toán 11

a) \(\left\{ \begin{array}{l}
BC \bot SA\\
BC \bot AB
\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)

⇒ Tam giác SBC vuông tại B.

b) \(\left\{ \begin{array}{l}
BH \bot AC\\
BH \bot SA
\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow \left( {SBH} \right) \bot \left( {SAC} \right)\)

c) d[B, (SAC)] = BH. Ta có:

\(\frac{1}{{B{H^2}}} = \frac{1}{{B{A^2}}} + \frac{1}{{B{C^2}}} = \frac{5}{{4{a^2}}} \Rightarrow BH = \frac{{2a\sqrt 5 }}{5}\)

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 3.50 trang 163 SBT Hình học 11 HAY thì click chia sẻ

YOMEDIA

Cho tứ diện \(ABCD\). Các điểm \(M\) và \(N\) lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp nào sau đây ?

bởi Mai Đào 25/02/2021

A. \(GM = GN\).

B. \(\overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \).

C. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).

\(D.\overrightarrow {PG} = \dfrac{1}{4}\left( {\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} } \right)\) với P là điểm bất kì.

Theo dõi (0) 1 Trả lời
Cho tứ diện \(ABCD\) có \(BCD\) là tam giác đều cạnh bằng \(a\), AB vuông góc với (BCD) và AB = 2a. Tang của góc giữa AC và mặt phẳng (ABD) bằng:

bởi My Van 26/02/2021

A.\(\sqrt 5 \)

B. 1

C. Không xác định.

D. \(\dfrac{{\sqrt {51} }}{{17}}\).

Theo dõi (0) 1 Trả lời
Cho hình chóp \(S.ABCD\), với \(O\) là giao điểm của \(AC\) và \(BD\). Mệnh đề nào sau đây đúng?

bởi Huong Giang 25/02/2021

A. Nếu ABCD là hình bình hành thì \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).

B. Nếu \(SA + SC = SB + SD\) thì ABCD là hình bình hành.

C. Nếu ABCD là hình bình hành thì \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).

D. Nếu \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) thì ABCD là hình bình hành.

Theo dõi (0) 1 Trả lời
Cho hình lập phương \(ABCD.EFGH\), thực hiện phép toán \(\overrightarrow x = \overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CG} \).

bởi thuy linh 25/02/2021

A. \(\overrightarrow x = \overrightarrow {GE} \).

B. \(\overrightarrow x = \overrightarrow {CE} \).

C. \(\overrightarrow x = \overrightarrow {CH} \).

D. \(\overrightarrow x = \overrightarrow {EC} \).

Theo dõi (0) 1 Trả lời