Bài tập 3.52 trang 163 SBT Hình học 11

Lý thuyết10 Trắc nghiệm

69 BT SGK

238 FAQ

Giải bài 3.52 tr 163 SBT Hình học 11

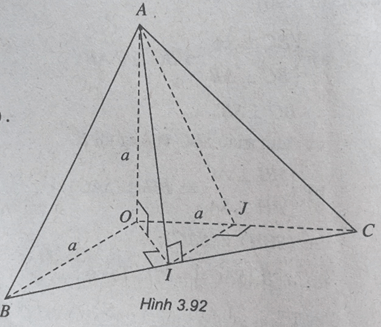
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC.

a) Chứng minh rằng: BC ⊥ (AOI), (OAI) ⊥ (ABC).

b) Tính góc giữa AB và mặt phẳng (AOI).

c) Tính góc giữa các đường thẳng AI và OB.

Hướng dẫn giải chi tiết

Giải sách bài tập Toán 11 | Giải sbt Toán 11

a) \(\left\{ \begin{array}{l}
BC \bot OA\\
BC \bot OI
\end{array} \right. \Rightarrow BC \bot \left( {OAI} \right) \Rightarrow \left( {ABC} \right) \bot \left( {OAI} \right)\).

b) + Xác định góc \(\alpha \) giữa AB và mặt phẳng (AOI):

Ta có: \(\left\{ \begin{array}{l}
A \in \left( {OAI} \right)\\
BI \bot \left( {OAI} \right)
\end{array} \right. \Rightarrow \left[ {\widehat {AB,\left( {OAI} \right)}} \right] = \widehat {BA}I = \alpha \)

+ Tính \(\alpha \):

Trong tam giác vuông BAI, ta có: \(\sin \alpha {\rm{ = }}\frac{1}{2} \Rightarrow \alpha = {30^0}\).

c) Xác định góc β giữa hai đường thẳng AI và OB:

Gọi J là trung điểm OC, ta có: IJ // OB và IJ ⊥ (AOC). Như vậy \(\left( {\widehat {AB,OB}} \right) = \widehat {\left( {AI,IJ} \right)} = \widehat {AIJ} = \beta \)

+ Tính góc β:

Trong tam giác IJA, ta có: \(\tan \beta = \frac{{AI}}{{IJ}} = \sqrt 5 \Rightarrow \beta = acr\tan \sqrt 5 \).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 3.52 trang 163 SBT Hình học 11 HAY thì click chia sẻ

YOMEDIA

Cho tứ diện \(ABCD\), \(O\) là trọng tâm tam giác \(BCD\). Tìm mệnh đề đúng.

bởi Dang Thi 25/02/2021

A. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {OA} \).

B. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AO} \).

C. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AO} \).

D. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {AO} \).

Theo dõi (0) 1 Trả lời
Cho hình hộp \(MNPQ.M’N’P’Q’\). Mệnh đề nào sau đây là mệnh đề đúng?

bởi Lê Văn Duyệt 25/02/2021

A. \(\overrightarrow {NQ'} = \overrightarrow {NM} + \overrightarrow {NP'} + \overrightarrow {NQ} \).

B. \(\overrightarrow {NQ'} = \overrightarrow {NM'} + \overrightarrow {NP} + \overrightarrow {NP'} \).

C. \(\overrightarrow {NQ'} = \overrightarrow {NM} + \overrightarrow {NQ} + \overrightarrow {NP'} \).

D. \(\overrightarrow {NQ'} = \overrightarrow {NM} + \overrightarrow {NP} + \overrightarrow {NN'} \).

Theo dõi (0) 1 Trả lời
Cho hình tứ diện \(ABCD\) có \(AB, BC, CD\) đôi một vuông góc . Mặt phẳng (ABD) vuông góc với mặt phẳng nào cua tứ diện ?

bởi hi hi 26/02/2021

A. (ACD).

B.(ABC).

C. (BCD).

D. Không có mặt phẳng nào .

Theo dõi (0) 1 Trả lời
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng \(\alpha \). Tan của góc giữa mặt bên và mặt đay bằng:

bởi Nguyễn Lệ Diễm 25/02/2021

A. \(\tan \alpha \).

B. \(\cot \alpha \).

C. \(\sqrt 2 \tan \alpha \).

D. \(\dfrac{{\sqrt 2 }}{{2\tan \alpha }}\).

Theo dõi (0) 1 Trả lời