Giải bài 3.45 tr 162 SBT Hình học 11
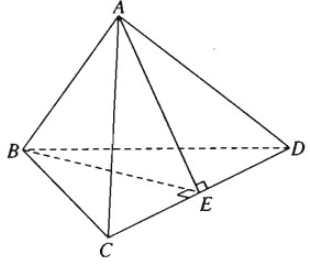
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi AC2 + BD2 = AD2 + BC2
Hướng dẫn giải chi tiết
Giả sử AB ⊥ CD ta chứng minh AC2 + BD2 = AD2 + BC2
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE.
Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
AC2 = AE2 + CE2
BD2 = BE2 + ED2
BC2 = AE2 + EC2
AD2 = AE2 + ED2
Từ đó ta suy ra AC2 + BD2 = AD2 + BC2
Ngược lại nếu tứ diện ABCD có AC2 + BD2 = AD2 + BC2 thì AC2 − AD2 = BC2 − BD2.
+ Nếu AC2 − AD2 = BC2 − BD2 = k2 thì trong mp(ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho \(I{H^2} = \frac{{{k^2}}}{{2CD}}\).
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
+ Nếu AC2 − AD2 = BC2 − BD2 = −k2 thì ta có và đưa về trường hợp xét như trên AD2 − AC2 = BD2 − BC2 = −k2.
-- Mod Toán 11 HỌC247
-


Cho hình chóp \(S. ABCD\) có đáy là tam giác đều cạnh a, \(SA \bot (ABC)\,,SA = \dfrac{a}{2}\). Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
bởi Thùy Trang
 25/02/2021
25/02/2021
A. 00
B. 450
C. 600
D. 900
Theo dõi (0) 1 Trả lời -


Cho hình hộp \(ABCD. A’B’C’D’\) có tất cả các cạnh bằng nhau. Điều nào sau đây sai?
bởi thu phương
 26/02/2021
26/02/2021
A. \(AC \bot B'D'\).
B. ACC’A’ là hình thoi.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Theo dõi (0) 1 Trả lời -


Cho hình lập phương \(ABCD. A’B’C’D’\). Mặt phẳng \((ACC’A’)\) vuông góc với mặt phẳng nào sau đây:
bởi Nguyễn Tiểu Ly
 26/02/2021
26/02/2021
A. (ABCD).
B.(CDD’C’).
C. (BDC’).
D. (A’BD).
Theo dõi (0) 1 Trả lời -


Cho hình lập phương \(ABCD.EFGH\), góc giữa hai đường thẳng \(AB\) và GH là:
bởi Mai Trang
 25/02/2021
25/02/2021
A. 00
B. 450
C. 1800
D. 900
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.43 trang 161 SBT Hình học 11
Bài tập 3.44 trang 162 SBT Hình học 11
Bài tập 3.46 trang 162 SBT Hình học 11
Bài tập 3.47 trang 162 SBT Hình học 11
Bài tập 3.49 trang 163 SBT Hình học 11
Bài tập 3.50 trang 163 SBT Hình học 11
Bài tập 3.51 trang 163 SBT Hình học 11
Bài tập 3.52 trang 163 SBT Hình học 11
Bài tập 3.53 trang 163 SBT Hình học 11
Bài tập 3.54 trang 164 SBT Hình học 11
Bài tập 3.55 trang 164 SBT Hình học 11
Bài tập 3.56 trang 164 SBT Hình học 11
Bài tập 3.57 trang 164 SBT Hình học 11
Bài tập 3.58 trang 164 SBT Hình học 11
Bài tập 3.59 trang 165 SBT Hình học 11
Bài tập 3.60 trang 165 SBT Hình học 11
Bài tập 3.61 trang 165 SBT Hình học 11
Bài tập 3.62 trang 165 SBT Hình học 11
Bài tập 3.63 trang 165 SBT Hình học 11
Bài tập 3.64 trang 165 SBT Hình học 11
Bài tập 3.65 trang 165 SBT Hình học 11
Bài tập 3.66 trang 166 SBT Hình học 11
Bài tập 3.67 trang 166 SBT Hình học 11
Bài tập 3.68 trang 166 SBT Hình học 10
Bài tập 3.69 trang 166 SBT Hình học 11
Bài tập 3.70 trang 167 SBT Hình học 11
Bài tập 3.71 trang 167 SBT Hình học 11
Bài tập 3.72 trang 167 SBT Hình học 11
Bài tập 3.73 trang 168 SBT Hình học 11
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC