Bài tập 1 trang 120 SGK Hình học 11 NC

Lý thuyết10 Trắc nghiệm

69 BT SGK

238 FAQ

Tứ diện OABC có OA = OB = OC = a và \(\widehat {AOB} = \widehat {AOC} = {60^0},\widehat {BOC} = {90^0}\)

a. Chứng tỏ rằng ABC là tam giác vuông và OA ⊥ BC

b. Tìm đường vuông góc chung IJ của OA và BC ; tính khoảng cách giữa hai đường thẳng OA và BC.

c. Chứng minh rằng hai mặt phẳng (ABC) và (OBC) vuông góc với nhau.

Hướng dẫn giải chi tiết

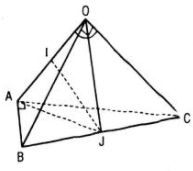
a) Vì \(\widehat {AOB} = \widehat {AOC} = {60^0}\)

OA = OB = OC = a

Nên AB = AC = a

Suy ra ΔABC = ΔOBC

Vậy tam giác ABC vuông cân tại A

Gọi J là trung điểm của BC thì OJ ⊥ BC, AJ ⊥ BC nên OA ⊥ BC.

b) Gọi I là trung điểm của OA, do OJ = AJ nên JI ⊥ OA, mà JI ⊥ BC, vậy IJ là đường vuông góc chung của OA và BC.

\(\begin{array}{l}
I{J^2} = O{J^2} - O{I^2}\\
= {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}
\end{array}\)

\(\begin{array}{*{20}{l}}
\begin{array}{l}
I{J^2} = O{J^2} - O{I^2}\\
= {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}
\end{array}\\
{ \Rightarrow d\left( {OA;BC} \right)\frac{a}{2}}
\end{array}\)

c) Từ các kết quả trên ta có :

OJ ⊥ BC, AJ ⊥ BC, IJ = \(\frac{1}{2}OA\)

Vậy góc giữa mp(OBC) và mp(ABC) bằng góc \(\widehat {OJA}\) và \(\widehat {OJA} = {90^0}\), do đó mp(OBC) ⊥ mp(ABC).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1 trang 120 SGK Hình học 11 NC HAY thì click chia sẻ

YOMEDIA

CM nếu tổng độ dài 2 đường trung bình...thì tứ giác là 1 hình bình hành

bởi ngọc trang 01/11/2018

Gọi đoạn nối trung điểm hai cạnh đối diện của một tứ giác lồi là đường trung bình của tứ giác đó. Chứng minh rằng nếu tổng độ dài hai đường trung bình của một tứ giác bằng nửa chu vi thì tứ giác đó là một hình bình hành

Theo dõi (0) 1 Trả lời
Chứng minh DA/cos(BDC)=DB/cos(CDA)=DC/cos(ADB)

bởi Việt Long 01/11/2018

Cho tứ diện ABCD. Gọi E, F,G lần lượt là trung điểm các cạnh DA, DB, DC và H, I, K tương ứng là trung điểm BC, CA, AB. Biết rằng EH=FI=GK. Chứng minh rằng :
\(\frac{DA}{\cos\widehat{BDC}}=\frac{DB}{\cos\widehat{CDA}}=\frac{DC}{\cos\widehat{ADB}}\)

Theo dõi (0) 1 Trả lời
Xác định và tính độ dài đoạn vuông góc chung của AB' và BC' biết AB=a, AC=a căn 2

bởi hành thư 01/11/2018

Cho hình lăng trụ đứng ABC.A'B'C' có hai đáy là tam giác vuông tại A, A', AB = a, AC=\(a\sqrt{2}\) và AA'=\(a\sqrt{3}\). Xác định và tính độ dài đoạn vuông góc chung của AB' và BC'

Theo dõi (0) 1 Trả lời
Chứng minh EGFH là hình bình hành, biết ABE, CDF là các tam giác đều

bởi thanh hằng 01/11/2018

Cho tứ giác lồi ABCD. Lấy các cạnh AB, CD làm đáy, dựng ra ngoài hai tam giác đều ABE, CDF. Lấy các cạnh BC, DA làm đáy, dựng vào trong hai tam giác đều BCG, DAH (tam giác BCG và tứ giác ABCD nằm về cùng một phía của đường thẳng BC, tam giá DAH và tứ giác ABCD nằm về cùng một phía của đường thẳng DA). Chứng minh rằng tứ giác EGFH là một hình bình hành

Theo dõi (0) 1 Trả lời