Giải bài 3.47 tr 162 SBT Hình học 11
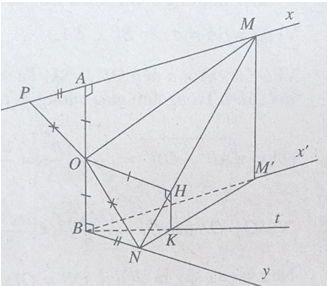
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN.
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc ∠x'By.
c) Chứng minh điểm H nằm trên một đường tròn cố định.
Hướng dẫn giải chi tiết
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Ta có ΔOMP = ΔOMN (c.c.c) ⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có HK // MM’ với K ∈ NM’.
Khi đó \(\frac{{KM'}}{{KN}} = \frac{{HM}}{{HN}} = \frac{{AM}}{{BN}} = \frac{{BM'}}{{BN}}\)
Do đó đối với \(\Delta BNM’\) đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β).
Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mp cố định (β) = (AB, BK)
-- Mod Toán 11 HỌC247
-


Cho hình chóp \(S. ABCD\) có đáy là tam giác đều cạnh a, \(SA \bot (ABC)\,,SA = \dfrac{a}{2}\). Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
bởi Bảo khanh
 26/02/2021
26/02/2021
A. 00
B. 450
C. 600
D. 900.
Theo dõi (0) 1 Trả lời -


Cho tứ diện \(ABCD\) có \(AB, AC, AD\) đôi một vuông góc với nhau. Khi đó góc giữa AB và CD bằng:
bởi Phí Phương
 25/02/2021
25/02/2021
A. 450
B. 600
C. 900
D. 300
Theo dõi (0) 1 Trả lời -


Cho hình tứ diện \(ABCD\) có \(AB , BC, CD\) đôi một vuông góc . Điểm cách đều bốn điểm \(A, B, C, D\) là:
bởi Hoang Viet
 26/02/2021
26/02/2021
A. Trung điểm J của AB.
B. Trung điểm I của BC.
C. Trung điểm M của AD.
D. Trung điểm N của CD.
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Véc tơ nào sau đây là véc tơ chỉ phương của đường thẳng \(AB\) ?
bởi thuy linh
 25/02/2021
25/02/2021
A. \(\overrightarrow {A'C'} \).
B. \(\overrightarrow {A'C} \).
C. \(\overrightarrow {A'B'} \).
D. \(\overrightarrow {A'B} \).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.45 trang 162 SBT Hình học 11
Bài tập 3.46 trang 162 SBT Hình học 11
Bài tập 3.49 trang 163 SBT Hình học 11
Bài tập 3.50 trang 163 SBT Hình học 11
Bài tập 3.51 trang 163 SBT Hình học 11
Bài tập 3.52 trang 163 SBT Hình học 11
Bài tập 3.53 trang 163 SBT Hình học 11
Bài tập 3.54 trang 164 SBT Hình học 11
Bài tập 3.55 trang 164 SBT Hình học 11
Bài tập 3.56 trang 164 SBT Hình học 11
Bài tập 3.57 trang 164 SBT Hình học 11
Bài tập 3.58 trang 164 SBT Hình học 11
Bài tập 3.59 trang 165 SBT Hình học 11
Bài tập 3.60 trang 165 SBT Hình học 11
Bài tập 3.61 trang 165 SBT Hình học 11
Bài tập 3.62 trang 165 SBT Hình học 11
Bài tập 3.63 trang 165 SBT Hình học 11
Bài tập 3.64 trang 165 SBT Hình học 11
Bài tập 3.65 trang 165 SBT Hình học 11
Bài tập 3.66 trang 166 SBT Hình học 11
Bài tập 3.67 trang 166 SBT Hình học 11
Bài tập 3.68 trang 166 SBT Hình học 10
Bài tập 3.69 trang 166 SBT Hình học 11
Bài tập 3.70 trang 167 SBT Hình học 11
Bài tập 3.71 trang 167 SBT Hình học 11
Bài tập 3.72 trang 167 SBT Hình học 11
Bài tập 3.73 trang 168 SBT Hình học 11
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC