Bài tập 4 trang 120 SGK Hình học 11 NC
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC).
Chứng minh rằng \(si{n^2}\alpha = si{n^2}\beta + si{n^2}\gamma \)
Hướng dẫn giải chi tiết
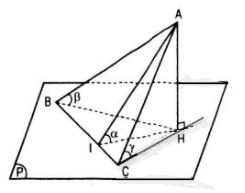
Kẻ AH ⊥ mp(P) và AI ⊥ BC
Thì \(\beta = \widehat {ABH},\gamma = \widehat {ACH},\alpha = \widehat {AIH}\)
Vì ΔABC vuông ở A nên:
\(\begin{array}{*{20}{l}}
{\frac{1}{{A{I^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}}\\
{ \Rightarrow \frac{{A{H^2}}}{{A{I^2}}} = \frac{{A{H^2}}}{{A{B^2}}} + \frac{{A{H^2}}}{{A{C^2}}}}\\
{hay{\mkern 1mu} {\mkern 1mu} {{\sin }^2}\alpha = {{\sin }^2}\beta + {{\sin }^2}\gamma }
\end{array}\)
-- Mod Toán 11 HỌC247
-


Cho hình hộp ABCD.A'B'C'D'. Xét M thuộc BB', N thuộc Cd sao cho BM : MB' = CN : ND và gọi I, J theo thứ tự là trungd diểm BC, D'A'. Chứng minh rằng M, N, I, J đồng phẳng.
Theo dõi (0) 3 Trả lời -


Trong mặt phẳng cho góc xOy và một điểm A cố định. Một đường tròn \(\omega\) đi qua O và A cắt tại các tia Ox, Oy theo thứ tự tại M, N. Chứng minh rằng khi \(\omega\) thay đổi, trung điểm MN luôn nằm trên một đường thẳng cố định
Theo dõi (0) 1 Trả lời -


Trên các cạnh BC, CA, AB của tam giác ABC tương ứng lấy các điểm A1, B1, C1. Gọi Ga, Gb, Gc theo thứ tự là trọng tâm các tam giác AB1C1, C1A1B, A1B1C và G, G1, G2 là trọng tâm của các tam giác ABC, A1B1C1, GaGbGc theo thứ tự đó. Chứng minh rằng G, G1, G2 thẳng hàng.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC. Xét điểm M trên tian AB, điểm N trên tia AC sao cho AB = m và AC = (m+1). AN với m>0 nào đó. Chứng minh rằng các đường thẳng MN luôn đi qua một điểm cố định
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC







