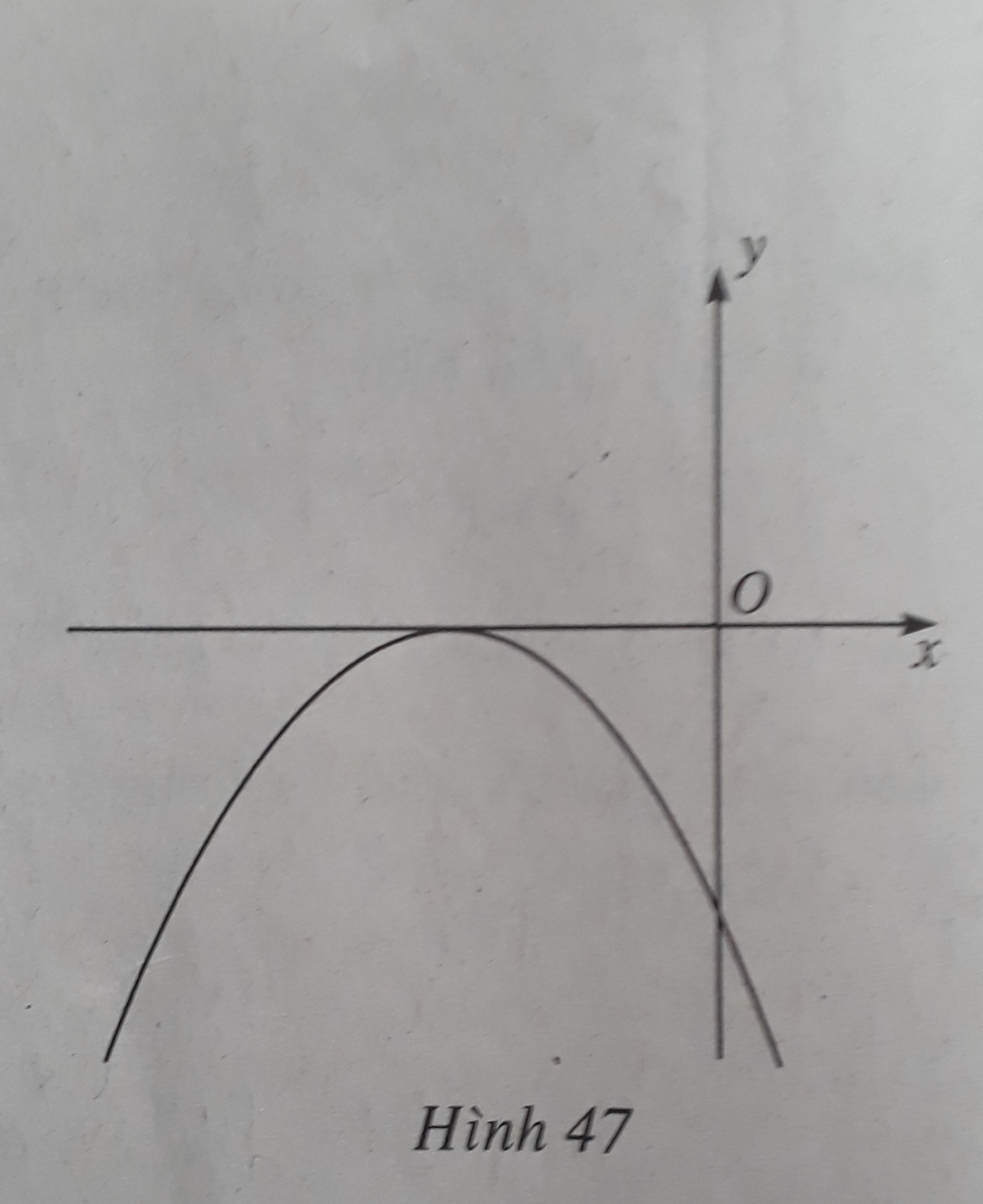Phần hướng dẫn giải bài tập Toán 10 Bài 5 Dấu của tam thức bậc hai sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
-
Bài tập 1 trang 105 SGK Đại số 10
Xét dấu các tam thức bậc hai
a) 5x2−3x+1;5x2−3x+1;
b) −2x2+3x+5;−2x2+3x+5;
c) x2+12x+36;x2+12x+36;
d) (2x−3)(x+5).(2x−3)(x+5).
-
Bài tập 2 trang 105 SGK Đại số 10
Lập bảng xét dấu các biểu thức sau
a) f(x)=(3x2−10x+3)(4x−5);f(x)=(3x2−10x+3)(4x−5);
b) f(x)=(3x2−4x)(2x2−x−1);f(x)=(3x2−4x)(2x2−x−1);
c) f(x)=(4x2−1)(−8x2+x−3)(2x+9);f(x)=(4x2−1)(−8x2+x−3)(2x+9);
d) f(x)=(3x2−x)(3−x2)4x2+x−3.f(x)=(3x2−x)(3−x2)4x2+x−3.
-
Bài tập 3 trang 105 SGK Đại số 10
Giải các bất phương trình sau
a) 4x2−x+1<0;4x2−x+1<0;
b) −3x2+x+4≥0;−3x2+x+4≥0;
c) 1x2−4<33x2+x−4;1x2−4<33x2+x−4;
d) x2−x−6≤0.x2−x−6≤0.
-
Bài tập 4 trang 105 SGK Đại số 10
Tìm các giá trị của tham số m để các phương trình sau vô nghiệm
a) (m−2)x2+2(2m−3)x+5m−6=0;(m−2)x2+2(2m−3)x+5m−6=0;
b) (3−m)x2−2(m+3)x+m+2=0.(3−m)x2−2(m+3)x+m+2=0.
-
Bài tập 4.51 trang 121 SBT Toán 10
Xét dấu của các tam thức bậc hai sau:
a) 2x2+5x+22x2+5x+2
b) 4x2−3x−14x2−3x−1
c) −3x2+5x+1−3x2+5x+1
d) 3x2+x+53x2+x+5
-
Bài tập 4.52 trang 121 SBT Toán 10
Giải các bất phương trình sau:
a) x2 - 2x + 3 > 0;
b) x2 + 9 > 6x.
-
Bài tập 4.53 trang 121 SBT Toán 10
Giải các bất phương trình sau:
a) 6x2 - x - 2 ≥ 0;
b) x23+3x+6<0x23+3x+6<0
-
Bài tập 4.54 trang 122 SBT Toán 10
Giải các bất phương trình sau:
a) x2+1x2+3x−10<0x2+1x2+3x−10<0
b) 10−x5+x2>1210−x5+x2>12
-
Bài tập 4.55 trang 122 SBT Toán 10
Giải các bất phương trình sau:
a) x+1x−1+2>x−1xx+1x−1+2>x−1x
b) 1x+1+2x+3<3x+21x+1+2x+3<3x+2
-
Bài tập 4.56 trang 122 SBT Toán 10
Giải các hệ bất phương trình sau:
a) {x2≥4x(2x−1)2<9{x2≥4x(2x−1)2<9
b) {2x−3<(x+1)(x−2)x2−x≤6{2x−3<(x+1)(x−2)x2−x≤6
-
Bài tập 4.57 trang 122 SBT Toán 10
Giải các hệ bất phương trình sau:
a) {x2≥4(2x−1)2≤9{x2≥4(2x−1)2≤9
b) {2x−3≤(x+1)(x−2)x2−x<6{2x−3≤(x+1)(x−2)x2−x<6
-
Bài tập 4.58 trang 122 SBT Toán 10
Giải các bất phương trình (ẩn m) sau:
a) 2m2−m−5>02m2−m−5>0
b) −m2+m+9>0−m2+m+9>0
-
Bài tập 4.59 trang 122 SBT Toán 10
Giải các bất phương trình (ẩn m) sau:
a) (2m - 1)2 - 4(m + 1)(m - 2) ≥ 0
b) m2 - (2m - 1)(m + 1) < 0
-
Bài tập 4.60 trang 122 SBT Toán 10
Giải các hệ bất phương trình (ẩn m) sau:
a) {(2m−1)2−4(m2−m)≥01m2−m>02m−1m2−m>0⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩(2m−1)2−4(m2−m)≥01m2−m>02m−1m2−m>0
b) {(m−2)2−(m+3)(m−1)≥0m−2m+3>0m−1m+3>0⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩(m−2)2−(m+3)(m−1)≥0m−2m+3>0m−1m+3>0
-
Bài tập 4.61 trang 122 SBT Toán 10
Giải các hệ bất phương trình (ẩn m) sau:
a) {2m−1>0m2−(m−2)(2m−1)<0{2m−1>0m2−(m−2)(2m−1)<0
b) {m2−m−2>0(2m−1)2−4(m2−m−2)≤0{m2−m−2>0(2m−1)2−4(m2−m−2)≤0
-
Bài tập 4.62 trang 122 SBT Toán 10
Tìm các giá trị của tham số m để các tam thức bậc hai sau có dấu không đổi (không phụ thuộc vào x).
a) f(x) = 2x2 - (m + 2)x + m2 - m + 1
b) f(x) = (m2 - m - 1)x2 - (2m - 1)x + 1
-
Bài tập 4.63 trang 122 SBT Toán 10
Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm phân biệt trái dấu
a) (m2 - 1)x2 + (m + 3)x + (m2 + m) = 0
b) x2 - (m3 + m - 2)x + m2 + m - 5 = 0.
-
Bài tập 4.64 trang 123 SBT Toán 10
Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm dương phân biệt
a) x2 - 2x + m2 + m + 3 = 0;
b) (m2 + m + 3)x2 + (4m2 + m + 2)x + m = 0
-
Bài tập 4.65 trang 123 SBT Toán 10
Với giá trị nào của tham số m hệ phương trình có nghiệm thỏa mãn điều kiện x > 0, y < 0?
{2x−(m2+m+1)y=−m2−9m4x+(2m2+1)y=1{2x−(m2+m+1)y=−m2−9m4x+(2m2+1)y=1
-
Bài tập 4.66 trang 123 SBT Toán 10
Tìm các giá trị của tham số m để các bất phương trình sau nghiệm đúng với mọi x
5x2 - x + m > 0
-
Bài tập 4.67 trang 123 SBT Toán 10
Tìm các giá trị của tham số m để các bất phương trình sau nghiệm đúng với mọi x
m(m + 2)x2 + 2mx + 2 > 0
-
Bài tập 4.68 trang 123 SBT Toán 10
Tìm m để bất phương trình sau vô nghiệm
5x2 - x + m ≤ 0
-
Bài tập 4.69 trang 123 SBT Toán 10
Tìm m để phương trình sau có hai nghiệm dương phân biệt
(m2 + m + 1)x2 + (2m - 3)x + m - 5 = 0
-
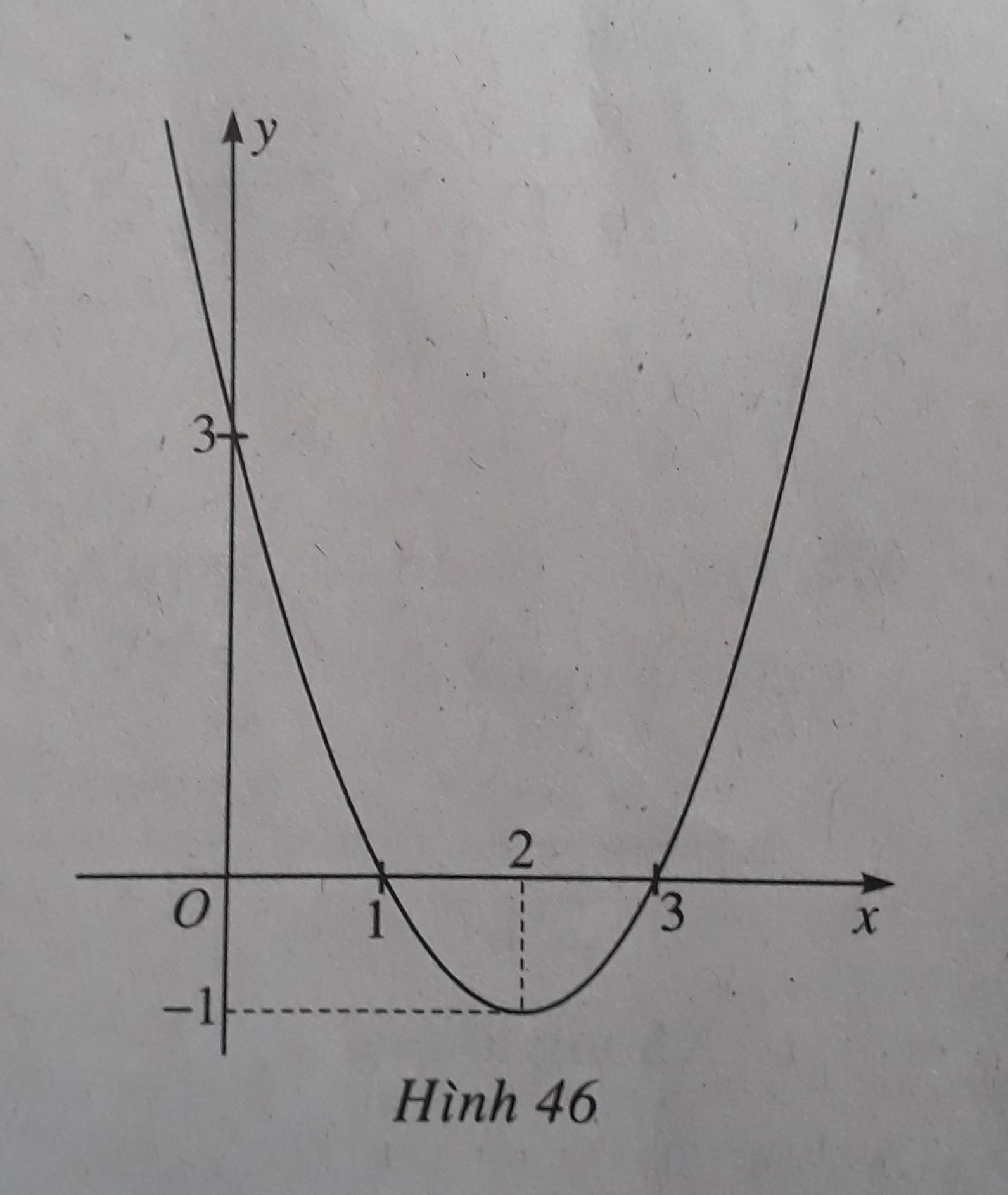
Bài tập 4.70 trang 123 SBT Toán 10
Đồ thị hàm số y = f(x) = x2 - 4x + 3 được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình x2 - 4x + 3 > 0
A. x < 1
B. x ≥ 1
C. 1 < x < 3
D. (-∞; 1) ∪ (3; +∞)
-
Bài tập 4.71 trang 124 SBT Toán 10
Đồ thị hàm số y = f(x) = ax2 + bx + c được cho trong hình 47. Kí hiệu Δ = b2 - 4ac là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
-
Bài tập 4.72 trang 124 SBT Toán 10
Tập nghiệm của bất phương trình - 3x2 + x + 4 ≥ 0 là:
A. S = ∅
B. S = (-∞; -1] ∪ [4343; +∞]
C. S = [-1; 4343]
D. S = (-∞; +∞)
-
Bài tập 4.73 trang 124 SBT Toán 10
Tìm tập xác định của hàm số
y=√x2+x−2x2−1y=√x2+x−2x2−1
A. x < -2; x ≤ -2;
B. x ≤ -2; x ≥ -1;
C. x ≤ -2; x ≤ -2;
D. x ≤ -2; -1 < x < 1; x > 1.
-
Bài tập 4.74 trang 124 SBT Toán 10
Tìm các giá trị của tham số m để phương trình mx2 + 2(2m - 1)x + m + 2 = 0 vô nghiệm
A. 3−√63<m<3+√633−√63<m<3+√63
B. Không tồn tại m
C. m < 112112
D. m ≠ 0; m < 112112
-
Bài tập 4.75 trang 124 SBT Toán 10
Tìm các giá trị của tham số m để bất phương trình mx2 - (2m - 1)x + 1 < 0
A. 4−2√34<m<4+2√344−2√34<m<4+2√34
B. 4−2√3<m<4+2√34−2√3<m<4+2√3
C. Không tồn tại m
D. 4−2√34<m<04−2√34<m<0
-
Bài tập 49 trang 140 SGK Toán 10 NC
Xét dấu các tam thức bậc hai sau:
a) 3x2 - 2x + 1
b) - x2 + 4x – 1
c) x2−√3x+34x2−√3x+34
d) (1−√2)x2−2x+1+√2(1−√2)x2−2x+1+√2
-
Bài tập 50 trang 140 SGK Toán 10 NC
Tìm các giá trị của m để mỗi biểu thức sau luôn dương:
a) (m2+2)x2 - 2(m+1)x + 1
b) (m+2)x2 + 2(m+2)x + m + 3
-
Bài tập 51 trang 141 SGK Toán 10 NC
Tìm các giá trị của m để mỗi biểu thức sau luôn âm.
a) −x2+2m√2x−2m2−1−x2+2m√2x−2m2−1
b) (m−2)x2−2(m−3)x+m−1(m−2)x2−2(m−3)x+m−1
-
Bài tập 52 trang 141 SGK Toán 10 NC
Chứng minh định lý về dấu của tam thức bậc 2.
Hướng dẫn: Với các trường hợp Δ < 0 và Δ = 0, sử dụng hệ thức đã biết:
f(x)=a[(x+b2a)2−Δ4a2]f(x)=a[(x+b2a)2−Δ4a2]
Hay af(x)=a2[(x+b2a)2−Δ4a2]af(x)=a2[(x+b2a)2−Δ4a2]
Trong trường hợp Δ > 0, sử dụng hệ thức đã biết:
f(x) = a(x – x1)(x – x2) hay af(x) = a2(x – x1)(x – x2)
trong đó x1 và x2 là hai nghiệm của tam thức bậc hai f(x)
-
Bài tập 53 trang 145 SGK Toán 10 NC
Giải các bất phương trình
a) - 5x2 + 4x + 12 < 0
b) 16x2 + 40x +25 < 0
c) 3x2 - 4x+4 ≥ 0
d) x2 - x - 6 ≤ 0
-
Bài tập 54 trang 145 SGK Toán 10 NC
Giải các bất phương trình sau:
a) x2−9x+14x2−5x+4>0x2−9x+14x2−5x+4>0
b) −2x2+7x+7x2−3x−10≤−1−2x2+7x+7x2−3x−10≤−1
c) (2x + 1)(x2 + x – 30) ≥ 0
d) x4 – 3x2 ≤ 0
-
Bài tập 55 trang 145 SGK Toán 10 NC
Tìm các giá trị của m để mỗi phương trình sau đây có nghiệm.
a) (m-5)x2 - 4mx + m – 2 = 0 (1)
b) (m+1)x2 + 2(m-1)x + 2m – 3 = 0
-
Bài tập 56 trang 145 SGK Toán 10 NC
Giải các hệ phương trình
a) {2x2+9x+7>0x2+x−6<0{2x2+9x+7>0x2+x−6<0
b) {2x2+9x+7>0x2+x−6<0{2x2+9x+7>0x2+x−6<0
c) {−2x2−5x+4<0−x2−3x+10≥0{−2x2−5x+4<0−x2−3x+10≥0
d) {2x2+x−6>03x2−10x+3>0{2x2+x−6>03x2−10x+3>0
-
Bài tập 57 trang 146 SGK Toán 10 NC
Tìm các giá trị m để các phương trình có nghiệm:
x2 + (m - 2)x - 2m + 3 = 0
-
Bài tập 58 trang 146 SGK Toán 10 NC
Chứng minh rằng các phương trình sau vô nghiệm dù m lấy bất kỳ giá trị nào.
a) x2 - 2(m + 1)x + 2m2 + m + 3 = 0
b) (m2 + 1)x2 + 2(m + 2)x + 6 = 0
-
Bài tập 59 trang 146 SGK Toán 10 NC
Tìm m để bất phương trình sau:
(m – 1)2 – 2(m + 1)x + 3(m – 2) > 0 nghiệm đúng với mọi x ∈ R
-
Bài tập 60 trang 146 SGK Toán 10 NC
Giải các bất phương trình:
a) x4−x2x2+5x+6≤0x4−x2x2+5x+6≤0
b) 1x2−5x+4<1x2−7x+101x2−5x+4<1x2−7x+10
-
Bài tập 61 trang 146 SGK Toán 10 NC
Tìm tập xác định của mỗi hàm số sau:
a) y=√(2x+5)(1−2x)y=√(2x+5)(1−2x)
b) y=√x2+5x+42x2+3x+1y=√x2+5x+42x2+3x+1
-
Bài tập 62 trang 146 SGK Toán 10 NC
Giải các hệ bất phương trình:
a) {4x−3<3x+4x2−7x+10≤0{4x−3<3x+4x2−7x+10≤0
b) {2x2+9x−7>0x2+x−6≤0{2x2+9x−7>0x2+x−6≤0
c) {x2−9<0(x−1)(3x2+7x+4)≥0{x2−9<0(x−1)(3x2+7x+4)≥0
-
Bài tập 63 trang 146 SGK Toán 10 NC
Tìm các giá trị của a sao cho với mọi x, ta luôn có:
−1≤x2+5x+a2x2−3x+2<7−1≤x2+5x+a2x2−3x+2<7
-
Bài tập 64 trang 146 SGK Toán 10 NC
Tìm các giá trị của m để hệ bất phương trình sau có nghiệm:
{x2+2x−15<0(m+1)x≥3{x2+2x−15<0(m+1)x≥3
-
Bài tập 65 trang 151 SGK Toán 10 NC
Giải các phương trình vầ bất phương trình sau:
a) |x2 – 5x + 4| = x2 + 6x + 5
b) |x – 1| = 2x – 1
c) |-x2 + x – 1| ≤ 2x + 5
d) |x2 – x| ≤ |x2 – 1|
-
Bài tập 66 trang 151 SGK Toán 10 NC
Giải các phương trình sau:
a) √2x2+4x−1=x+1√2x2+4x−1=x+1
b) √4x2+101x+64=2(x+10)√4x2+101x+64=2(x+10)
c) √x2+2x=−2x2−4x+3√x2+2x=−2x2−4x+3
d) √(x+1)(x+2)=x2+3x−4√(x+1)(x+2)=x2+3x−4
-
Bài tập 67 trang 151 SGK Toán 10 NC
Giải các bất phương trình:
a) √x2+x−6<x−1√x2+x−6<x−1
b) √2x−1≤2x−3√2x−1≤2x−3
c) √2x2−1>1−x√2x2−1>1−x
d) √x2−5x−14≥2x−1√x2−5x−14≥2x−1
-
Bài tập 68 trang 151 SGK Toán 10 NC
Tìm tập xác định của mỗi hàm số sau:
a) y=√|x2+3x−4|−x+8y=√|x2+3x−4|−x+8
b) y=√x2+x+1|2x−1|−x−2y=√x2+x+1|2x−1|−x−2
c) y=√1x2−7x+5−1x2+2x+5y=√1x2−7x+5−1x2+2x+5
d) √√x2−5x−14−x+3√√x2−5x−14−x+3
-
Bài tập 69 trang 154 SGK Toán 10 NC
Giải các phương trình và bất phương trình sau:
a) |x2−2x+1|=2∣∣x2−2x+1∣∣=2
b) |3x+4x−2|≤3∣∣3x+4x−2∣∣≤3
c) |2x−3x−3|≥1∣∣2x−3x−3∣∣≥1
d) |2x+3|=|4−3x||2x+3|=|4−3x|
-
Bài tập 70 trang 154 SGK Toán 10 NC
Giải các bất phương trình sau:
a) |x2 – 5x + 4| ≤ x2 + 6x + 5
b) 4x2 + 4x - |2x + 1| ≥ 5
-
Bài tập 71 trang 154 SGK Toán 10 NC
Giải các phương trình sau:
a) √5x2−6x−4=2(x−1)√5x2−6x−4=2(x−1)
b) √x2+3x+12=x2+3x√x2+3x+12=x2+3x
-
Bài tập 72 trang 154 SGK Toán 10 NC
Giải các bất phương trình
a) √x2+6x+8≤2x+3√x2+6x+8≤2x+3
b) 2x−4√x2−3x−10>12x−4√x2−3x−10>1
c) 6√(x−2)(x−32)≤x2−34x+486√(x−2)(x−32)≤x2−34x+48
-
Bài tập 73 trang 154 SGK Toán 10 NC
Giải các bất phương trình sau:
a) √x2−x−12≥x−1√x2−x−12≥x−1
b) √x2−4x−12>2x+3√x2−4x−12>2x+3
c) √x+51−x<1√x+51−x<1
-
Bài tập 74 trang 154 SGK Toán 10 NC
Tìm các giá trị của m sao cho phương trình:
x4 + (1 - 2m)x2 + m2 – 1 = 0
a) Vô nghiệm
b) Có hai nghiệm phân biệt
c) Có bốn nghiệm phân biệt
-
Bài tập 75 trang 154 SGK Toán 10 NC
Tìm các giá trị của a sao cho phương trình:
(a-1)x4 - ax2 + a2 – 1 = 0 có ba nghiệm phân biệt.