Bài tập 51 trang 141 SGK Toán 10 NC
Tìm các giá trị của m để mỗi biểu thức sau luôn âm.
a) \( - {x^2} + 2m\sqrt 2 x - 2{m^2} - 1\)
b) \(\left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1\)
Hướng dẫn giải chi tiết
a) Vì a = - 1 < 0 nên:
\(\begin{array}{l}
- {x^2} + 2m\sqrt 2 x - 2{m^2} - 1 < 0,\forall x \in R\\
\Leftrightarrow \Delta ' = 2{m^2} - \left( {2{m^2} + 1} \right) < 0\\
\Leftrightarrow - 1 < 0\,\,\left( {ld} \right)
\end{array}\)
Vậy với mọi m thì \( - {x^2} + 2m\sqrt 2 x - 2{m^2} - 1 < 0,\forall x \in R\)
b) Đặt \(f\left( x \right) = \left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1\)
Với m = 2 thì \(f(x) = 2x + 1\) không thỏa mãn điều kiện yêu cầu bài toán.
Với \(m \ne 2\) thì \(f\left( x \right) < 0,\forall x \in R\)
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
a < 0\\
\Delta ' < 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
m - 2 < 0\\
{\left( {m - 3} \right)^2} - \left( {m - 2} \right)\left( {m - 1} \right) < 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
m < 2\\
- 3m + 7 < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m < 2\\
m > \frac{7}{3}
\end{array} \right.
\end{array}\)
Ta không tìm được m thỏa mãn hệ thức trên.
Vậy không có giá trị m để \(f\left( x \right) < 0,\forall x \in R\)
-- Mod Toán 10 HỌC247
-


Bất phương trình ( m - 2) x2 + 2(m -1)x + m +1 <0 vô nghiệm khi và chỉ khi ?
Theo dõi (0) 8 Trả lời -


Giải bất phương trình -1<=(10x^2-3x-2)/(-x^2+3x-2)<1
bởi Đồng Thiên
 06/04/2020
06/04/2020
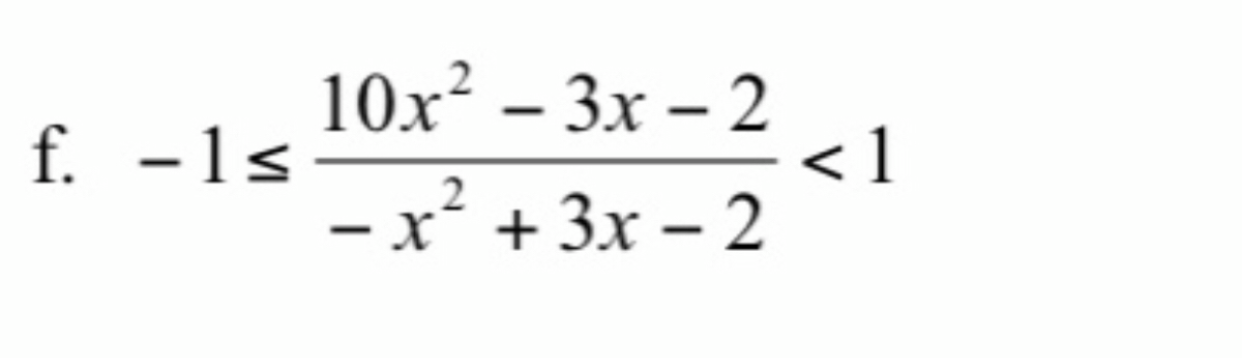 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính số phần tử của S?
bởi linh
 06/04/2020
Khoanh tròn
06/04/2020
Khoanh tròn Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 49 trang 140 SGK Toán 10 NC
Bài tập 50 trang 140 SGK Toán 10 NC
Bài tập 52 trang 141 SGK Toán 10 NC
Bài tập 53 trang 145 SGK Toán 10 NC
Bài tập 54 trang 145 SGK Toán 10 NC
Bài tập 55 trang 145 SGK Toán 10 NC
Bài tập 56 trang 145 SGK Toán 10 NC
Bài tập 57 trang 146 SGK Toán 10 NC
Bài tập 58 trang 146 SGK Toán 10 NC
Bài tập 59 trang 146 SGK Toán 10 NC
Bài tập 60 trang 146 SGK Toán 10 NC
Bài tập 61 trang 146 SGK Toán 10 NC
Bài tập 62 trang 146 SGK Toán 10 NC
Bài tập 63 trang 146 SGK Toán 10 NC
Bài tập 64 trang 146 SGK Toán 10 NC
Bài tập 65 trang 151 SGK Toán 10 NC
Bài tập 66 trang 151 SGK Toán 10 NC
Bài tập 67 trang 151 SGK Toán 10 NC
Bài tập 68 trang 151 SGK Toán 10 NC
Bài tập 69 trang 154 SGK Toán 10 NC
Bài tập 70 trang 154 SGK Toán 10 NC
Bài tập 71 trang 154 SGK Toán 10 NC
Bài tập 72 trang 154 SGK Toán 10 NC
Bài tập 73 trang 154 SGK Toán 10 NC





