Giải bài 4.51 tr 121 SBT Toán 10
Xét dấu của các tam thức bậc hai sau:
a) \(2{x^2} + 5x + 2\)
b) \(4{x^2} - 3x - 1\)
c) \( - 3{x^2} + 5x + 1\)
d) \(3{x^2} + x + 5\)
Hướng dẫn giải chi tiết
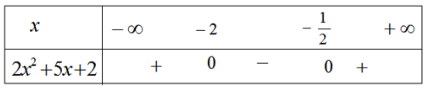
a) Đặt \(f(x) =2{x^2} + 5x + 2\)
Bảng xét dấu
Vậy \(f(x) > 0\) khi \(x \in \left( { - \infty ; - 2} \right) \cup \left( { - \frac{1}{2}; + \infty } \right)\) và \(f(x) < 0\) khi \(x \in \left( { - 2; - \frac{1}{2}} \right)\)
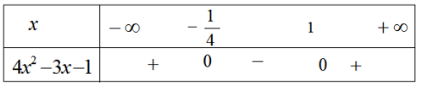 Vậy \(f(x) > 0\) khi \(x \in \left( { - \infty ; - \frac{1}{4}} \right) \cup \left( {1; + \infty } \right)\) và \(f(x) < 0\) khi \(x \in \left( { - \frac{1}{4};1} \right)\)
Vậy \(f(x) > 0\) khi \(x \in \left( { - \infty ; - \frac{1}{4}} \right) \cup \left( {1; + \infty } \right)\) và \(f(x) < 0\) khi \(x \in \left( { - \frac{1}{4};1} \right)\)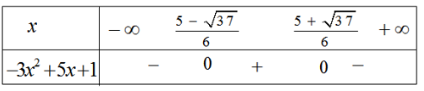 Vậy \(f(x) > 0\) khi \(x \in \left( {\frac{{ - 5 - \sqrt {37} }}{6};\frac{{ - 5 + \sqrt {37} }}{6}} \right)\) và \(f(x) < 0\) khi \(x \in \left( { - \infty ;\frac{{ - 5 - \sqrt {37} }}{6}} \right) \cup \left( {\frac{{ - 5 + \sqrt {37} }}{6}; + \infty } \right)\)
Vậy \(f(x) > 0\) khi \(x \in \left( {\frac{{ - 5 - \sqrt {37} }}{6};\frac{{ - 5 + \sqrt {37} }}{6}} \right)\) và \(f(x) < 0\) khi \(x \in \left( { - \infty ;\frac{{ - 5 - \sqrt {37} }}{6}} \right) \cup \left( {\frac{{ - 5 + \sqrt {37} }}{6}; + \infty } \right)\)Vậy 3x2 + x + 5 > 0, ∀x
-- Mod Toán 10 HỌC247
-


Hãy giải bất phương trình, hệ bất phương trình (ẩn m) sau: \({(2m - 1)^2} - 4(m + 1)(m - 2) \ge 0\)
bởi Thúy Vân
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Hãy giải bất phương trình, hệ bất phương trình (ẩn m) sau: \( - {m^2} + m + 9 > 0.\)
bởi Lê Minh Trí
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Hãy giải bất phương trình, hệ bất phương trình (ẩn m) sau: \(2{m^2} - m - 5 > 0;\)
bởi Minh Hanh
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Giải bất phương trình cho sau đây: \(\left\{ \begin{array}{l}2x - 3 < (x + 1)(x - 2)\\{x^2} - x \le 6\end{array} \right.\)
bởi Song Thu
 26/04/2022
Theo dõi (0) 1 Trả lời
26/04/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3 trang 105 SGK Đại số 10
Bài tập 4 trang 105 SGK Đại số 10
Bài tập 4.52 trang 121 SBT Toán 10
Bài tập 4.53 trang 121 SBT Toán 10
Bài tập 4.54 trang 122 SBT Toán 10
Bài tập 4.55 trang 122 SBT Toán 10
Bài tập 4.56 trang 122 SBT Toán 10
Bài tập 4.57 trang 122 SBT Toán 10
Bài tập 4.58 trang 122 SBT Toán 10
Bài tập 4.59 trang 122 SBT Toán 10
Bài tập 4.60 trang 122 SBT Toán 10
Bài tập 4.61 trang 122 SBT Toán 10
Bài tập 4.62 trang 122 SBT Toán 10
Bài tập 4.63 trang 122 SBT Toán 10
Bài tập 4.64 trang 123 SBT Toán 10
Bài tập 4.65 trang 123 SBT Toán 10
Bài tập 4.66 trang 123 SBT Toán 10
Bài tập 4.67 trang 123 SBT Toán 10
Bài tập 4.68 trang 123 SBT Toán 10
Bài tập 4.69 trang 123 SBT Toán 10
Bài tập 4.70 trang 123 SBT Toán 10
Bài tập 4.71 trang 124 SBT Toán 10
Bài tập 4.72 trang 124 SBT Toán 10
Bài tập 4.73 trang 124 SBT Toán 10
Bài tập 4.74 trang 124 SBT Toán 10
Bài tập 4.75 trang 124 SBT Toán 10
Bài tập 49 trang 140 SGK Toán 10 NC
Bài tập 50 trang 140 SGK Toán 10 NC
Bài tập 51 trang 141 SGK Toán 10 NC
Bài tập 52 trang 141 SGK Toán 10 NC
Bài tập 53 trang 145 SGK Toán 10 NC
Bài tập 54 trang 145 SGK Toán 10 NC
Bài tập 55 trang 145 SGK Toán 10 NC
Bài tập 56 trang 145 SGK Toán 10 NC
Bài tập 57 trang 146 SGK Toán 10 NC
Bài tập 58 trang 146 SGK Toán 10 NC
Bài tập 59 trang 146 SGK Toán 10 NC
Bài tập 60 trang 146 SGK Toán 10 NC
Bài tập 61 trang 146 SGK Toán 10 NC
Bài tập 62 trang 146 SGK Toán 10 NC
Bài tập 63 trang 146 SGK Toán 10 NC
Bài tập 64 trang 146 SGK Toán 10 NC
Bài tập 65 trang 151 SGK Toán 10 NC
Bài tập 66 trang 151 SGK Toán 10 NC
Bài tập 67 trang 151 SGK Toán 10 NC
Bài tập 68 trang 151 SGK Toán 10 NC
Bài tập 69 trang 154 SGK Toán 10 NC
Bài tập 70 trang 154 SGK Toán 10 NC
Bài tập 71 trang 154 SGK Toán 10 NC
Bài tập 72 trang 154 SGK Toán 10 NC
Bài tập 73 trang 154 SGK Toán 10 NC