Giải bài 2 tr 49 sách GK Toán Hình lớp 12
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Hướng dẫn giải chi tiết bài 2
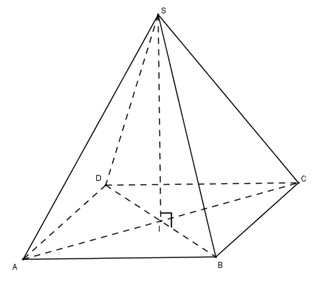
Gọi I = AC ∩ BD. Ta thấy AC = a√2 = BD,
SA = SC = a, nên SA2 + SC2 = AC2. Vậy điểm S nhìn AC dưới một góc vuông. Các điểm B và D cũng nhìn AC dưới một góc vuông.
Vậy mặt cầu ngoại tiếp hình chóp là mặt cầu đường kính AC. Tâm của cầu là điểm I và bán kính R = 
. Ta thấy rằng điểm I cũng là chân đường cao hạ từ đỉnh S xuống đáy.
-- Mod Toán 12 HỌC247
-
Chứng minh có một mặt cầu tiếp xúc với bốn mặt của hình tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện).
bởi Nguyễn Lê Thảo Trang
06/06/2021
Chứng minh có một mặt cầu tiếp xúc với bốn mặt của hình tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện).
Theo dõi (0) 1 Trả lời -
Cho tứ diện ABCD với AB = CD = c, AC = BD = b, AD = BC = a. Tính diện tích mặt cầu ngoại tiếp tứ diện.
bởi trang lan
06/06/2021
Cho tứ diện ABCD với AB = CD = c, AC = BD = b, AD = BC = a. Tính diện tích mặt cầu ngoại tiếp tứ diện.
Theo dõi (0) 1 Trả lời -
Hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh cùng bằng \(a\). Gọi \(A’, B’, C’, D’\) lần lượt là trung điểm của \(SA, SB, SC, SD\). Chứng minh rằng các điểm \(A, B, C, D, A’, B’, C’, D’\) cùng thuộc một mặt cầu và tính thể tích khối cầu đó.
bởi Phan Thị Trinh
06/06/2021
Hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh cùng bằng \(a\). Gọi \(A’, B’, C’, D’\) lần lượt là trung điểm của \(SA, SB, SC, SD\). Chứng minh rằng các điểm \(A, B, C, D, A’, B’, C’, D’\) cùng thuộc một mặt cầu và tính thể tích khối cầu đó.
Theo dõi (0) 1 Trả lời -
Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).
bởi thu phương
06/06/2021
Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).
Theo dõi (0) 1 Trả lời -
Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện \(ABCD\) thì \(AB + CD = AC + BD = AD + BC\).
bởi Dang Tung
07/06/2021
Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện \(ABCD\) thì \(AB + CD = AC + BD = AD + BC\).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 49 SGK Hình học 12
Bài tập 3 trang 49 SGK Hình học 12
Bài tập 4 trang 49 SGK Hình học 12
Bài tập 5 trang 49 SGK Hình học 12
Bài tập 6 trang 49 SGK Hình học 12
Bài tập 7 trang 49 SGK Hình học 12
Bài tập 8 trang 49 SGK Hình học 12
Bài tập 9 trang 49 SGK Hình học 12
Bài tập 10 trang 49 SGK Hình học 12
Bài tập 2.13 trang 60 SBT Hình học 12
Bài tập 2.14 trang 60 SBT Hình học 12
Bài tập 2.15 trang 60 SBT Hình học 12
Bài tập 2.16 trang 60 SBT Hình học 12
Bài tập 2.17 trang 61 SBT Hình học 12
Bài tập 2.18 trang 61 SBT Hình học 12
Bài tập 2.19 trang 61 SBT Hình học 12
Bài tập 2.20 trang 61 SBT Hình học 12
Bài tập 2.21 trang 61 SBT Hình học 12
Bài tập 2.22 trang 61 SBT Hình học 12
Bài tập 2.23 trang 61 SBT Hình học 12
Bài tập 1 trang 45 SGK Hình học 12 NC
Bài tập 2 trang 45 SGK Hình học 12 NC
Bài tập 3 trang 45 SGK Hình học 12 NC
Bài tập 4 trang 45 SGK Hình học 12 NC
Bài tập 5 trang 45 SGK Hình học 12 NC
Bài tập 6 trang 45 SGK Hình học 12 NC
Bài tập 7 trang 45 SGK Hình học 12 NC
Bài tập 8 trang 45 SGK Hình học 12 NC
