Giải bài 10 tr 49 sách GK Toán Hình lớp 12
Cho hình chóp S.ABC có bốn đỉnh đếu nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo bởi mặt cầu đó
Hướng dẫn giải chi tiết bài 10
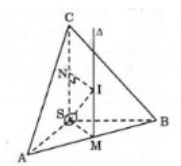
Gọi I là tâm cầu ngoại tiếp hình chóp tam giác S.ABC. Hạ IJ vuông góc (SAB), vì J cách đều 3 điểm S, A, B nên J cũng cách đều 3 điểm S, A, B.
Vì tam giác SAB vuông đỉnh S nên J là trung điểm của AB.
Ta có \(SJ = \frac{1}{2}AB = \frac{1}{2}\sqrt {{a^2} + {b^2}} \).
Do SC vuông góc (SAB) nên IJ // SC.
Gọi H là trung điểm SC, ta có SH = IJ = \(\frac{c}{2}\).
Do vậy, \(IS^2 = IJ^2 + SJ^2 = \frac{(a^2 + b^2 + c^2)}{4}\) và bán kính hình cầu ngoại tiếp S.ABC là
\(r=IS=\frac{1}{2}\sqrt{a^2+b^2+c^2}\)
Diện tích mặt cầu là:
\(S = 4 \pi r^2 = \pi (a^2 + b^2 + c^2)\) (đvdt)
Thể tích khối cầu là:
\(V=\frac{4}{3}\pi ^3=\frac{1}{6}\pi (a^2+b^2+c^2)^{\frac{3}{2}}= \frac{1}{6}\pi (a^2+b^2+c^2)\sqrt{a^2+b^2+c^2}\)(đvtt)
-- Mod Toán 12 HỌC247
-


Trong không gian Oxyz cho mặt phẳng (a):2x-2y-z+3=0 điểm I;(2;1-1) mặt cầu tâm I tiếp xúc(a) có bán kính
bởi Thị Yến
 22/05/2020
22/05/2020
Cho em cách giải bài này
Theo dõi (0) 1 Trả lời -


Thể tích khối cầu ngoại tiếp hình lăng trụ đều có tất cả các cạnh là 2a.căn 3
bởi Lam Tuyet Anh
 20/05/2020
Theo dõi (0) 0 Trả lời
20/05/2020
Theo dõi (0) 0 Trả lời -


Trong không gian với hệ tọa độ Oxyz, tìm m để phương trình \({x^2} + {y^2} + {z^2} - 2mx + 2\left( {m + 1} \right)y - 4z + 1 = 0\) là phương trình mặt cầu
bởi Trịnh Lan Trinh
 20/05/2020
20/05/2020
M.n giúp em giải câu này với ạ
Theo dõi (1) 1 Trả lời -


Viết phương trình mặt cầu (S)?
bởi phamminhtu
 17/04/2020
17/04/2020
Giúp em
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


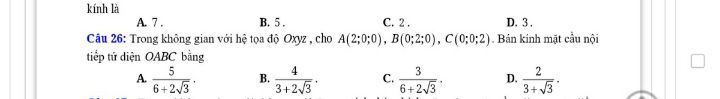 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 8 trang 49 SGK Hình học 12
Bài tập 9 trang 49 SGK Hình học 12
Bài tập 2.13 trang 60 SBT Hình học 12
Bài tập 2.14 trang 60 SBT Hình học 12
Bài tập 2.15 trang 60 SBT Hình học 12
Bài tập 2.16 trang 60 SBT Hình học 12
Bài tập 2.17 trang 61 SBT Hình học 12
Bài tập 2.18 trang 61 SBT Hình học 12
Bài tập 2.19 trang 61 SBT Hình học 12
Bài tập 2.20 trang 61 SBT Hình học 12
Bài tập 2.21 trang 61 SBT Hình học 12
Bài tập 2.22 trang 61 SBT Hình học 12
Bài tập 2.23 trang 61 SBT Hình học 12
Bài tập 1 trang 45 SGK Hình học 12 NC
Bài tập 2 trang 45 SGK Hình học 12 NC
Bài tập 3 trang 45 SGK Hình học 12 NC
Bài tập 4 trang 45 SGK Hình học 12 NC
Bài tập 5 trang 45 SGK Hình học 12 NC
Bài tập 6 trang 45 SGK Hình học 12 NC
Bài tập 7 trang 45 SGK Hình học 12 NC
Bài tập 8 trang 45 SGK Hình học 12 NC





