Giải bài 5 tr 49 sách GK Toán Hình lớp 12
Từ một điểm M nằm nằm bên ngoài mặt cầu S( O; r) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.
a) Chứng minh rằng MA>MB = MC>MD.
b) GỌi MO = d. Tính MA>MB theo r và d.
Hướng dẫn giải chi tiết bài 5
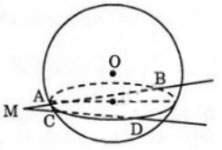
Câu a:
Gọi (P) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng (P) cắt mặt cầu S(O;r) theo một đường tròn tâm I, là hình chiếu vuông góc của O lên mặt phẳng (P).
Xét hai tam giác MAD và MCB có góc 
chung nên hai tam giác đó đồng dạng.
Vì vậy: 
=> MA.MB = MC.MD.
Câu b:
Đặt MO = d, ta có Oi vuông góc với (P) và ta có:
MO2= MI2 = OI2 và OA2 = OI2 + IA2
Hạ IH vuông góc AB, ta có H là trung điểm của AB.
Ta có MA = MH - HA; MB = MH + HB = MH + HA.
Nên MA.MB =
MH2 – HA2 = (MH2 + HI2) – (HA2 + IH2)
= MI2 – IA2 = ( MI2 + OI2) – (IA2 + OI2)
= MO2 – OẢ2
= d2 – r2
Vậy MA.MB = d2 – r2
-- Mod Toán 12 HỌC247
-
Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng:
bởi Trần Hoàng Mai
28/05/2020
A. 4π(cm2) B. 16π/3(cm2)
C. 16π(cm2) D. 64π(cm2)
Theo dõi (0) 3 Trả lời -
Theo dõi (0) 1 Trả lời -
Viết phương trình mặt cầu có đường kính AB với A (4; -3; 7), B(2; 1; 3)
bởi Trần Bảo Việt
25/05/2020
Theo dõi (0) 2 Trả lời -
Theo dõi (0) 1 Trả lời
