Giải bài 7 tr 49 sách GK Toán Hình lớp 12
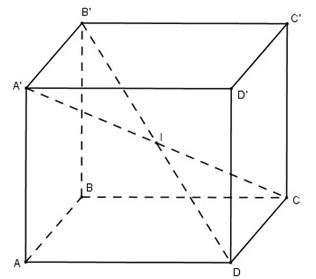
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
b) Tính bán kính của đường tròn là giao tuyến cưa mặt phẳng (ABCD) với mặt cầu trên.
Hướng dẫn giải chi tiết bài 7
Câu a:
Trong hình hộp chữ nhật, bốn đường chéo AC", BD', CA" và DB" căt nhau tại điểm I là trung điểm của mỗi đường.
Vì 4 đường chéo trong hình hộp chữ nhật bằng nhau, nên điểm I cách đề 8 đỉnh của hình hộp chữ nhật. Nó là tâm của mặt cầu ngoại tiếp hình hộp.
Vì AB = b, AD = c, AA' = a nên bán kính mặt cầu\(R=\frac{1}{2}.A'C=\frac{1}{2}.\sqrt{a^2+b^2+c^2}\).
Câu b:
Giao tuyến của mặt phẳng ABCD với mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là hai đwòng tròn ngoại tiếp hình chữ nhật ABCD. Nên bán kính của đường trong giao tuyến là
\(r=\frac{1}{2}.AC=\frac{1}{2}.\sqrt{b^2+c^2}\)
-- Mod Toán 12 HỌC247
-


Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({x^2} + {y^2} + {z^2} - 2x - 2y - 4z + 5 = 0\)
bởi Trần Hoàng Mai
 29/05/2020
29/05/2020
Trong các khẳng định sau, khẳng định nào sai?
A. Mặt cầu (S) có tâm I(1;1;2) và đường kính có độ dài bằng 2.
B. Phương trình chính tắc của mặt cầu (S) là: (x - 1)2 + (y - 1)2 + (z - 2)2 = 1
C. Diện tích của mặt cầu (S) là π
D. Thể tích của khối cầu (S) là 4π/3
Theo dõi (0) 4 Trả lời -


Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB = SB = a , SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là:
bởi Nguyễn Thanh Trà
 29/05/2020
Theo dõi (0) 4 Trả lời
29/05/2020
Theo dõi (0) 4 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD theo a
bởi Lê Gia Bảo
 29/05/2020
Theo dõi (0) 1 Trả lời
29/05/2020
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2AD = 2a, SA vuông góc với đáy, SA = a. Tính bán kính mặt cầu ngoại tiếp hình chóp
bởi Nguyễn Sơn Ca
 28/05/2020
Theo dõi (0) 2 Trả lời
28/05/2020
Theo dõi (0) 2 Trả lời -


Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a. Trong các điểm S, B, C điểm nào nằm trong mặt cầu tâm A bán kính 3a.
bởi Trịnh Lan Trinh
 28/05/2020
28/05/2020
A. Không điểm nào
B. Chỉ điểm S
C. Chỉ hai điểm B và C
D. Cả ba điểm
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 5 trang 49 SGK Hình học 12
Bài tập 6 trang 49 SGK Hình học 12
Bài tập 8 trang 49 SGK Hình học 12
Bài tập 9 trang 49 SGK Hình học 12
Bài tập 10 trang 49 SGK Hình học 12
Bài tập 2.13 trang 60 SBT Hình học 12
Bài tập 2.14 trang 60 SBT Hình học 12
Bài tập 2.15 trang 60 SBT Hình học 12
Bài tập 2.16 trang 60 SBT Hình học 12
Bài tập 2.17 trang 61 SBT Hình học 12
Bài tập 2.18 trang 61 SBT Hình học 12
Bài tập 2.19 trang 61 SBT Hình học 12
Bài tập 2.20 trang 61 SBT Hình học 12
Bài tập 2.21 trang 61 SBT Hình học 12
Bài tập 2.22 trang 61 SBT Hình học 12
Bài tập 2.23 trang 61 SBT Hình học 12
Bài tập 1 trang 45 SGK Hình học 12 NC
Bài tập 2 trang 45 SGK Hình học 12 NC
Bài tập 3 trang 45 SGK Hình học 12 NC
Bài tập 4 trang 45 SGK Hình học 12 NC
Bài tập 5 trang 45 SGK Hình học 12 NC
Bài tập 6 trang 45 SGK Hình học 12 NC
Bài tập 7 trang 45 SGK Hình học 12 NC
Bài tập 8 trang 45 SGK Hình học 12 NC