Phần hướng dẫn giải bài tập SGK bài Ôn tập chương V sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập về Đạo hàm từ SGK Đại số và Giải tích 11 Cơ bản & Nâng cao.
-
Bài tập 1 trang 176 SGK Đại số & Giải tích 11
Tìm đạo hàm của các hàm số sau:
a) \(y=\frac{x^3}{3}-\frac{x^2}{2}+x-5\)
b) \(y=\frac{2}{x}-\frac{4}{x^2}+\frac{5}{x^3}-\frac{6}{7x^4}\)
c) \(y=\frac{3x^2-6x+7}{4x}\)
d) \(y=\left ( \frac{2}{x}+3x \right )(\sqrt{x}-1)\)
e) \(y=\frac{1+\sqrt{x}}{1-\sqrt{x}}\)
f) \(y=\frac{-x^2+7x+5}{x^2-3x}.\)
-
Bài tập 2 trang 176 SGK Đại số & Giải tích 11
Tính đạo hàm của các hàm số sau
a) \(y=2\sqrt{x} .sinx-\frac{cosx}{x}\)
b) \(y= \frac{3cosx}{2x+1}\)
c) \(y= \frac{t^2+2cost}{sin t}\)
d) \(y=\frac{2cos\varphi -sin\varphi }{3sin\varphi +cos\varphi }\)
e) \(y=\frac{tanx}{sinx+2}\)
f) \(y=\frac{cotx}{2\sqrt{x}-1}\)
-
Bài tập 3 trang 176 SGK Đại số & Giải tích 11
Cho hàm số: \(f(x)=\sqrt{1+x}\). Tính \(f(3)+(x-3).f'(3).\)
-
Bài tập 4 trang 176 SGK Đại số & Giải tích 11
Cho hàm số \(f(x)=tan x\) và \(g(x)=\frac{1}{1-x}\). Tính \(\frac{f'(0)}{g'(0)}\).
-
Bài tập 5 trang 176 SGK Đại số & Giải tích 11
Giải phương trình f'(x) = 0, biết rằng:
\(f(x)=3x+\frac{60}{x}-\frac{64}{x^3}+5\)
-
Bài tập 6 trang 176 SGK Đại số & Giải tích 11
Cho \(f_1(x)=\frac{cosx}{x}, f_2(x)=xsinx.\) Tính \(\frac{f_1(1)}{f_2(1)}.\)
-
Bài tập 7 trang 176 SGK Đại số & Giải tích 11
Viết phương trình tiếp tuyến:
a) Của hypebol \(y=\frac{x+1}{x-1}\) tại điểm A(2;3);
b) Của đường cong \(y=x^3+4x^2-1\) tại điểm có hoành độ \(x_0=-1\)
c) Của Parabol \(y=x^2-4x+4\) tại điểm có tung độ \(y_0=1.\)
-
Bài tập 8 trang 177 SGK Đại số & Giải tích 11
Cho chuyển động thẳng xác định bởi phương trình: \(s=t^3-3t^2-9t\) trong đó t được tính bẳng giây và s được tính bằng mét.
a) Tính vận tốc của chuyển động khi t = 3s.
b) Tính gia tốc của chuyển động khi t = 3s.
c) Tính gia tốc tại thời điểm vận tốc triệt tiêu.
d) Tính vận tốc tại thời điểm gia tốc triệt tiêu.
-
Bài tập 9 trang 177 SGK Đại số & Giải tích 11
Cho hai hàm số \(y=\frac{1}{x\sqrt{2}}\) và \(y=\frac{x^2}{\sqrt{2}}\)
Viết phương trình tiếp tuyến với đồ thị của mỗi hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.
-
Bài tập 10 trang 177 SGK Đại số & Giải tích 11
Với \(g(x)=\frac{x^2-2x+5}{x-1}; g'(2)\) bằng:
(A) 1
(B) -3
(C) -5
(D) 0
-
Bài tập 11 trang 177 SGK Đại số & Giải tích 11
Nếu \(f(x)=sin^3x+x^2\) thì \(f''(\frac{\pi }{2})\) bằng:
(A) 0
(B) 1
(C) -2
(D) 5
-
Bài tập 12 trang 177 SGK Đại số & Giải tích 11
Giả sử \(h(x)=5(x+1)^3+4(x+1).\)
Tập nghiệm của phương trình h''(x) = 0 là:
(A) \([-1;2]\)
(B) \((-\infty ;0]\)
(C) \(\left \{ -1 \right \}\)
(D) \(\varnothing\)
-
Bài tập 13 trang 177 SGK Đại số & Giải tích 11
Cho \(f(x)=\frac{x^3}{3}+\frac{x^2}{2}+x.\)
Tập nghiệm của bất phương trình \(f'(x)\leq 0\) là:
(A) \(\varnothing\)
(B) \((0;+\infty )\)
(C) \([-2;2]\)
(D) \((-\infty ;+\infty )\)
-
Bài tập 5.112 trang 217 SBT Toán 11
Tìm đạo hàm của các hàm số sau:
-
Bài tập 5.113 trang 217 SBT Toán 11
Giải phương trình \(f'\left( x \right) = g\left( x \right),\) biết rằng:
-
Bài tập 5.114 trang 217 SBT Toán 11
Tìm đạo hàm của hàm số tại điểm đã chỉ ra?
a) \(f(x) = \frac{{\sqrt {x + 1} }}{{\sqrt {x + 1} + 1}},f\prime (0) = ?\)
b) \(y = {(4x + 5)^2},y\prime (0) = ?\)
c) \(g(x) = \sin 4x\cos 4x,g\prime \left( {\frac{\pi }{3}} \right) = ?\)
-
Bài tập 5.115 trang 217 SBT Toán 11
Chứng minh rằng \(f'\left( x \right) > 0,\forall x \in R\), nếu
-
Bài tập 5.116 trang 217 SBT Toán 11
Xác định a để \(f'\left( x \right) > 0,\forall x \in R\), biết rằng \(f(x) = {x^3} + (a - 1){x^2} + 2x + 1\)
-
Bài tập 5.117 trang 217 SBT Toán 11
Xác định a để \(g'\left( x \right) \ge 0,\forall x \in R\), biết rằng:
\(g(x) = \sin x - a\sin 2x - \frac{1}{3}\sin 3x + 2ax\)
-
Bài tập 5.118 trang 217 SBT Toán 11
Tìm hệ số góc của tiếp tuyến của đồ thị hàm số \(y = \tan x\) tại điểm có hoành độ
-
Bài tập 5.119 trang 218 SBT Toán 11
Trên đường cong \(y = 4{x^2} - 6x + 3\), hãy tìm điểm tại đó tiếp tuyến song song với đường thẳng
-
Bài tập 5.120 trang 218 SBT Toán 11
Đồ thị hàm số \(y = \frac{1}{{\sqrt 3 }}\sin 3x\) cắt trục hoành tại gốc tọa độ dưới một góc bao nhiêu độ (góc giữa trục hoành và tiếp tuyến của đồ thị tại giao điểm)?
-
Bài tập 5.121 trang 218 SBT Toán 11
Cho các hàm số
\(\begin{array}{l}
f\left( x \right) = {x^3} + b{x^2} + cx + d;\,\,\,\left( C \right)\\
g\left( x \right) = {x^2} - 3x - 1
\end{array}\)a) Xác định b, c, d sao cho đồ thị (C ) đi qua các điểm và \(f'\left( {\frac{1}{3}} \right) = \frac{5}{3}\)
b) Viết phương trình tiếp tuyến của (C ) tại điểm có hoành độ x0 = 1;
c) Giải phương trình \(f'\left( {\sin t} \right) = 3\)
d) Giải phương trình \(f''\left( {\cos t} \right) = g'\left( {\sin t} \right)\)
e) Tìm giới hạn \(\mathop {\lim }\limits_{z \to 0} \frac{{f\prime \prime (\sin 5z) + 2}}{{g\prime (\sin 3z) + 3}}\)
-
Bài tập 5.122 trang 218 SBT Toán 11
Chứng minh rằng tiếp tuyến của hypebol \(y = \frac{{{a^2}}}{x}\) lập thành với các trục tọa độ một tam giác có diện tích không đổi.
-
Bài tập 5.123 trang 218 SBT Toán 11
Chứng minh rằng nếu hàm số f(z) có đạo hàm đến cấp n thì \(\left[ {f\left( {ax + b} \right)} \right]_x^{\left( n \right)} = {a^n}f_z^{\left( n \right)}\left( {ax + b} \right)\)
-
Bài tập 5.124 trang 218 SBT Toán 11
Đạo hàm của hàm số y = x3 - 2x2 + x + 1 tại x = 0 bằng
A. 1 B. 0 C. 2 D. - 2
-
Bài tập 5.125 trang 218 SBT Toán 11
Hàm số \(y = \left\{ \begin{array}{l}
2x,\,\,\,x \ge 0\\
- 3x,\,x < 0
\end{array} \right.\) không có đạo hàm tạiA. x = 2 B. x = 1 C. x = 0 D. x = -1
-
Bài tập 5.126 trang 218 SBT Toán 11
Phương trình tiếp tuyến với đồ thị của hàm số tại là:
-
Bài tập 5.127 trang 218 SBT Toán 11
Đạo hàm của hàm số \(y = \frac{{2x}}{{\sin x}}\) là:
-
Bài tập 5.128 trang 219 SBT Toán 11
Cho \(f(x) = \frac{{{x^3}}}{3} - 2{x^2} + {m^2}x - 5\). Tìm tham số m để f′(x) > 0 với mọi x ∈ R
A. m > 2
B. m > 2 hoặc m < −2
C. m < −2
D. m ∈ R
-
Bài tập 5.129 trang 219 SBT Toán 11
Cho \({f\left( x \right) = \tan \left( {2{x^3} - 5} \right)}\). Tìm
-
Bài tập 5.130 trang 219 SBT Toán 11
Tìm nghiệm của phương trình \(f''\left( x \right) = 0\) biết \(f\left( x \right) = 3\cos x - \sqrt 3 \sin x\)
B. \(x = \frac{\pi }{6} + k\pi \)
\(x = \frac{\pi }{3} + k\pi \)
D. \(x = \frac{\pi }{6} + k\pi \)
-
Bài tập 5.131 trang 219 SBT Toán 11
Cho \(y = {\tan ^3}x\). Tìm
-
Bài tập 49 trang 220 SGK Toán 11 NC
Tìm đạo hàm của các hàm số sau :
a. \(y = \frac{{{x^4}}}{2} + \frac{{5{x^3}}}{3} - \sqrt {2x} + 1\)
b. \(y = \frac{{{x^2} + 3x - {a^2}}}{{x - 1}}\) (a là hằng số)
c. \(y = (2 - {x^2})\cos x + 2x\sin x\)
d. \(y = {\tan ^2}x + \tan {x^2}\)
-
Bài tập 50 trang 221 SGK Toán 11 NC
a. Chứng minh rằng \(\left( {\frac{1}{{{x^n}}}} \right)\prime = - \frac{n}{{{x^{n + 1}}}},\) trong đó n ϵ N*
b. Với x ≠ 0 và n ϵ N*, ta đặt \({x^{ - n}} = \frac{1}{{{x^n}}}\). Từ đó hãy so sánh đẳng thức trong câu a với công thức \({\left( {{x^n}} \right)^\prime } = n{x^{n - 1}}\) và nêu nhận xét.
-
Bài tập 51 trang 221 SGK Toán 11 NC
Tìm đạo hàm đến cấp được nêu kèm theo của các hàm số sau (n ϵ N*)
\(\begin{array}{*{20}{l}}
{a)y = \sin x,\:y'''}\\
{b)y = \sin x\sin 5x,{y^{(4)}}}\\
{c)y = {{(4 - x)}^5},{y^{(n)}}}\\
{d)y = \frac{1}{{2 + x}},{y^{(n)}}}\\
{e)y = \frac{1}{{2x + 1}},{y^{(n)}}}\\
{f)y = {{\cos }^2}x,{y^{(2n)}}}
\end{array}\) -
Bài tập 52 trang 221 SGK Toán 11 NC
Tính vi phân của hàm số \(y = \frac{1}{{{{(1 + tanx)}^2}}}\) tại điểm \(x = \frac{\pi }{6}\) ứng với \(\Delta x = \frac{\pi }{{360}}\) (tính chính xác đến hàng phần vạn).
-
Bài tập 53 trang 221 SGK Toán 11 NC
Gọi (C) là đồ thị của hàm số \(f(x) = {x^4} + 2{x^2} - 1\). Viết phương trình tiếp tuyến của (C) trong mỗi trường hợp sau :
a. Biết tung độ tiếp điểm bằng 2
b. Biết rằng tiếp tuyến song song với trục hoành
c. Biết rằng tiếp tuyến vuông góc với đường thẳng \(y = - \frac{1}{8}x + 3\)
d. Biết rằng tiếp tuyến đi qua điểm A(0 ; -6)
-
Bài tập 54 trang 221 SGK Toán 11 NC
Tìm một điểm trên đồ thị của hàm số \(y = \frac{1}{{x - 1}}\) sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2.
-
Bài tập 55 trang 221 SGK Toán 11 NC
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).
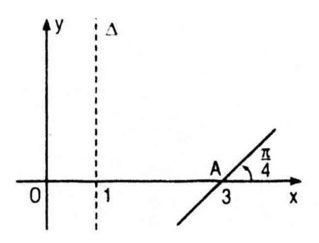
-
Bài tập 56 trang 221 SGK Toán 11 NC
Cho parabol (P) : y = x2. Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = - 2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.
-
Bài tập 57 trang 222 SGK Toán 11 NC
Một chất điểm chuyển động có phương trình S = t3 − 3t2 − 9t + 2, t > 0, t tính bằng giây (s) và S tính bằng mét (m)
a. Tính vận tốc tại thời điểm t = 2
b. Tính gia tốc tại thời điểm t = 3
c. Tính gia tốc tại thời điểm vận tốc bằng 0
d. Tính vận tốc tại thời điểm gia tốc bằng 0.
-
Bài tập 58 trang 222 SGK Toán 11 NC
Mỗi khẳng định sau đây đúng hay sai ?
a. Hàm số y = cotx có đạo hàm tại mọi điểm mà nó xác định
b. Hàm số \(y = \sqrt x \) có đạo hàm tại mọi điểm mà nó xác định
c. Hàm số y = |x| có đạo hàm tại mọi điểm mà nó xác định.
-
Bài tập 59 trang 222 SGK Toán 11 NC
Tiếp tuyến của đồ thị hàm số \(y = \frac{4}{{x - 1}}\) tại điểm với hoành độ x = -1 có phương trình là
A. y = −x–3
B. y = −x+2
C. y = x–1
D. y = x+2
-
Bài tập 60 trang 222 SGK Toán 11 NC
Tiếp tuyến của đồ thị hàm số \(y = \frac{1}{{\sqrt {2x} }}\) tại điểm với hoành độ \(x = \frac{1}{2}\) có phương trình là :
A. \(2x-2y = - 1\)
B. \(2x-2y = 1\)
C. \(2x + 2y = 3\)
D. \(2x + 2y = - 3\)
-
Bài tập 61 trang 222 SGK Toán 11 NC
Hàm số có đạo hàm bằng \(2x + \frac{1}{{{x^2}}}\) là :
A. \(y = \frac{{{x^3} + 1}}{x}\)
B. \(y = \frac{{{x^3} + 5x - 1}}{x}\)
C. \(y = \frac{{3\left( {{x^2} + x} \right)}}{{{x^3}}}\)
D. \(y = \frac{{2{x^2} + x - 1}}{x}\)
-
Bài tập 62 trang 223 SGK Toán 11 NC
Đạo hàm cấp 2010 của hàm số y = cosx là :
A. sinx
B. – sinx
C. cosx
D. – cosx
-
Bài tập 63 trang 223 SGK Toán 11 NC
Điền nội dung thích hợp vào chỗ trống.
a. Hàm số hợp của hàm số y = cotu và hàm số trung gian \(u = \sqrt x \) là y = …………….
b. Hàm số hợp của hàm số y = un và hàm số trung gian u = cosx + sinx là y = ………….
c. Hàm số y = tan3x là hàm số hợp của hàm số y = ………….. và hàm số trung gian u = ………….
d. Hàm số \(y = \sqrt {\cos x} \) là hàm số hợp của hàm số y = ………….. và hàm số trung gian u = ………….






