Giải bài 2 tr 25 sách GK Toán Hình lớp 12
Tính thể tích khối bát diện đều cạnh a.
Hướng dẫn giải chi tiết bài 2
Ta có:
\({V_{ABCDEF}} = {V_{ABCDE}} + {V_{FBCDE}} \)
\(= 2{V_{ABCDE}} = 2.\frac{1}{2}{S_{BCDE}}.AO\)
Với O là tâm hình vuông BCDE.
Vì AO vuông góc với mặt phẳng BCDO nên theo định lý Pi-ta-go ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} \)
\(= \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{a}{{\sqrt 2 }}\)
Vì BCDE là hình vuông cạnh a nên: \({S_{BCDE}} = {a^2}.\)
Do đó: \({V_{ABCDEF}} = \frac{2}{3}{a^2}.\frac{a}{{\sqrt 2 }} = \frac{{{a^3}\sqrt 3 }}{3}.\)
-- Mod Toán 12 HỌC247
-


Cho hình hộp \(ABCD.A’B’C’D’\). Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện \(ACB’D’\).
bởi Nguyễn Hồng Tiến
 05/06/2021
05/06/2021
Cho hình hộp \(ABCD.A’B’C’D’\). Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện \(ACB’D’\).
Theo dõi (0) 1 Trả lời -


Hãy tính thể tích khối bát diện đều cạnh \(a\).
bởi Mai Trang
 05/06/2021
05/06/2021
Hãy tính thể tích khối bát diện đều cạnh \(a\).
Theo dõi (0) 1 Trả lời -


Hãy tính thể tích khối tứ diện đều cạnh \(a\).
bởi Lê Minh Bảo Bảo
 05/06/2021
05/06/2021
Hãy tính thể tích khối tứ diện đều cạnh \(a\).
Theo dõi (0) 1 Trả lời -


Kim tự tháp Kê-ốp ở Ai Cập (h.1.27) được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Hãy tính thể tích của nó.
bởi thi trang
 05/06/2021
05/06/2021
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính thể tích khối chóp S.ABCD?
bởi quỳnh trang
 29/08/2020
29/08/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính thể tích khối chóp S.ABCD?
bởi Hoàng Lâm
 26/08/2020
26/08/2020
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều, SAB vuông góc mp đáy. M là trung điểm AD. Tính:
a) Thể tích khối chóp S.ABCD?
b)Thể tích khối chóp S.MABC?
Theo dõi (0) 9 Trả lời -


Tính thể tích khối chóp S.ABCD?
bởi khang Lưu Khang
 25/08/2020
25/08/2020
Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 2a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy . Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng 60 độ.
Vẽ hình giúp mình nha....
Theo dõi (0) 12 Trả lời -


Diện tích đáy của hình chóp tứ giác đều bằng bao nhiêu?
bởi Híp
 25/08/2020
25/08/2020
Một hình chóp tứ giác đều có góc tạo bởi mặt bên và mặt đáy bằng 60° và diện tích xung quanh \(=8a^2\). Tính S mặt đáy của hình chóp.
Theo dõi (0) 0 Trả lời -


Tính thể tích khối chóp S.ABCD?
bởi Như Quỳnh
 19/08/2020
19/08/2020
Giúp mình với ạ. Cảm ơn mn.
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Thể tích khối chọp S.ABC là bao nhiêu?
bởi Như Quỳnh
 19/08/2020
19/08/2020
Giải giúp mình câu này ạ.
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính thể tích khối chóp SABC?
bởi Thanh Tráng
 17/08/2020
17/08/2020
Tính thể tích khối chóp SABC có đáy vuông tại A. BC=a. SB=SC=\(\dfrac{a \sqrt 3}{2}\) . ( SBC) vuông góc với (ABC), mặt bên (SAB) tạo với mặt đáy góc 600.
Theo dõi (0) 8 Trả lời -


Câu 2
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Thể tích khối chóp S.ABCD tính theo a là bao nhiêu?
bởi Thị minh
 11/08/2020
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a cạnh bên hợp với đáy một góc 60 độ .Tính theo a thể tích khối chóp S.ABCDTheo dõi (0) 1 Trả lời
11/08/2020
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a cạnh bên hợp với đáy một góc 60 độ .Tính theo a thể tích khối chóp S.ABCDTheo dõi (0) 1 Trả lời -


Thể tích khối chóp S.ABCD bằng bao nhiêu?
bởi Đoàn Nguyễn Thanh Lam
 05/08/2020
05/08/2020
Câu 33
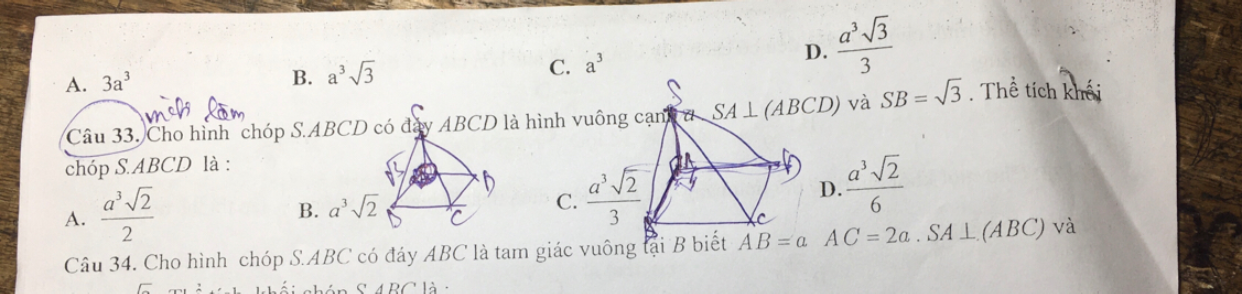 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Chứng minh: \(V= \frac{1}{6}abc.\sin \alpha \)?
bởi Lê Nguyệt Quế
 30/07/2020
30/07/2020
Mọi người giải giúp mình bài này với ạ
Cho tứ diện ABCD có AB=a, CD=b, khoảng cách giữa AB và CD bằng d và góc giữa AB và CD bằng
.Chứng minh: V=
1/6abc.sin
Theo dõi (0) 0 Trả lời -


Tính khoảng cách giữa hai đường thẳng A'B và B'C?
bởi Trinh Mỹ Duy
 29/07/2020
29/07/2020
Cho lăng trụ đứng ABCA'B'C' có đáy là tam giác đều cạnh a và cạnh bên bằng a căn 2. Tính khoảng cách giữa hai đường thẳng A'B và B'C.
Theo dõi (0) 0 Trả lời -


Tính thể tích S.ABCD?
bởi Nguyễn Phương Anh
 23/07/2020
23/07/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, các cạnh bên cùng tạo với mặt phẳng đáy những góc 60°. Tính VS.ABCD .
Theo dõi (0) 1 Trả lời -


Thể tích khối lăng trụ bằng bao nhiêu?
bởi Lê Kiều Mi
 02/07/2020
02/07/2020
Giúp e câu 37 ạ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Thể tích khối chóp S.ABC bằng bao nhiêu?
bởi thì bê
 30/06/2020
30/06/2020
Cho hình chóp S.ABC có SA vuông góc ABC tam giác ABC vuông tại C. AB =a căn 3; SC = a căn 5. Thể tích khối chóp S.ABC bằng
Theo dõi (0) 2 Trả lời -


Cho hình chóp có đáy là tam giác đều cạnh bằng a. Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng 2a. Thể tích của khối chóp có giá trị nhỏ nhất bằng bao nhiêu?
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt phẳng (SBC) tạo với đáy góc 600. Mặt bên (SAB) vuông góc với đáy, tam giác SAB cân tại S. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SA, BC.
bởi Nguyễn Thanh Trà
 30/05/2020
Theo dõi (0) 3 Trả lời
30/05/2020
Theo dõi (0) 3 Trả lời -


Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích xung quanh Sxq của hình trụ (T) là
bởi Lê Gia Bảo
 30/05/2020
Theo dõi (0) 3 Trả lời
30/05/2020
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 1 trang 25 SGK Hình học 12
Bài tập 3 trang 25 SGK Hình học 12
Bài tập 4 trang 25 SGK Hình học 12
Bài tập 5 trang 26 SGK Hình học 12
Bài tập 6 trang 26 SGK Hình học 12
Bài tập 1.10 trang 18 SBT Hình học 12
Bài tập 1.11 trang 18 SBT Hình học 12
Bài tập 1.12 trang 18 BT Hình học 12
Bài tập 1.13 trang 18 SBT Hình học 12
Bài tập 1.14 trang 18 SBT Hình học 12
Bài tập 1.15 trang 19 SBT Hình học 12
Bài tập 1.16 trang 19 SBT Hình học 12
Bài tập 1.17 trang 19 SBT Hình học 12
Bài tập 15 trang 28 SGK Hình học 12 NC
Bài tập 16 trang 28 SGK Hình học 12 NC
Bài tập 17 trang 28 SGK Hình học 12 NC
Bài tập 18 trang 28 SGK Hình học 12 NC
Bài tập 19 trang 28 SGK Hình học 12 NC
Bài tập 20 trang 28 SGK Hình học 12 NC
Bài tập 21 trang 28 SGK Hình học 12 NC
Bài tập 22 trang 28 SGK Hình học 12 NC
Bài tập 23 trang 29 SGK Hình học 12 NC




.PNG)


