Giải bài 3.39 tr 76 SBT Toán 10
Tìm điều kiện của mỗi phương trình sau:
a) \(\sqrt { - 3x + 2} = \frac{2}{{x + 1}}\)
b) \(\sqrt {x - 2} + x = 3{x^2} + 1 - \sqrt { - x - 4} \)
c) \(\frac{{x+4}}{{\sqrt {3{x^2} + 6x + 11} }} = \sqrt {2x + 1} \)
d) \(\frac{{\sqrt { - 3x + 2} }}{{{x^2} - 9}} = x + 2\)
Hướng dẫn giải chi tiết
a) ĐKXĐ: \(\left\{ \begin{array}{l}
- 3x + 2 \ge 0\\
x + 1 \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \le \frac{2}{3}\\
x \ne - 1
\end{array} \right.\)
b) ĐKXĐ: \(\left\{ \begin{array}{l}
x - 2 \ge 0\\
- x - 4 \ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ge 2\\
x \le - 4
\end{array} \right. \Leftrightarrow x \in \emptyset \)
c) ĐKXĐ: \(\left\{ \begin{array}{l}
3{x^2} + 6x + 11 > 0\\
2x + 1 \ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \in R\\
x \ge - \frac{1}{2}
\end{array} \right. \Leftrightarrow x \ge - \frac{1}{2}\)
d) ĐKXĐ: \(\left\{ \begin{array}{l}
x + 4 \ge 0\\
{x^2} - 9 \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ge - 4\\
x \ne \pm 3
\end{array} \right.\)
-- Mod Toán 10 HỌC247
-


Xác định m để phương trình \(\dfrac{{2x - m + 1}}{{\sqrt {x - 1} }} - 4\sqrt {x - 1} = \dfrac{{x - 2m + 1}}{{\sqrt {x - 1} }}\) có nghiệm.
bởi Tuyet Anh
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Giải và biện luận phương trình \(\left| {mx + 2} \right| = \left| {2x - m} \right|\).
bởi Huy Hạnh
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Cho phương trình \(m{x^2} - 2\left( {m + 1} \right)x + m + 2 = 0\). Xác định các giá trị nguyên của m để phương trình có hai nghiệm phân biệt sao cho tổng các nghiệm là một số nguyên.
bởi Lê Trung Phuong
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Cho phương trình \(m{x^2} - 2\left( {m + 1} \right)x + m + 2 = 0\). Xác định m để phương trình có một nghiệm bằng 2. Tìm nghiệm còn lại.
bởi Spider man
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Giải và biện luận phương trình \(\dfrac{{x - m}}{{x - 1}} = {m^2}\) theo tham số m.
bởi Nguyễn Lê Tín
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \(\left( {{x^2} + x - 2} \right)\left( {{x^2} + x - 3} \right) = 12\).
bởi Lê Tấn Vũ
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Cho phương trình \(\left( {m - 1} \right){x^2} - 2mx + m + 2 = 0\). Với giá trị nào của m thì phương trình có hai nghiệm trái dấu?
bởi Tran Chau
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Cho phương trình \(\left( {m - 1} \right){x^2} - 2mx + m + 2 = 0\). Xác định m để phương trình có nghiệm.
bởi Hữu Nghĩa
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình \(\left( {m - 2} \right){x^2} - 2x + 1 - 2m = 0\) có nghiệm duy nhất. Tổng của các phần tử trong S bằng:
bởi Kim Ngan
 22/01/2021
22/01/2021
A. 5/2
B. 3
C. 7/2
D. 9/2
Theo dõi (0) 2 Trả lời -


Để hai đồ thị \(y = {x^2}\; - 2x + 3\) và \(y = {x^2} - m\) có hai điểm chung thì:
bởi con cai
 21/01/2021
21/01/2021
A. m = -3,5
B. m < -3,5
C. m > -3,5
D. m ≥ -3,5
Theo dõi (0) 2 Trả lời -


Cho phương trình bậc hai: \({x^2}--2\left( {m + 6} \right)x + {m^2} = 0\). Với giá trị nào của m thì phương trình có nghiệm kép và tìm nghiệm kép đó?
bởi cuc trang
 22/01/2021
22/01/2021
A. m = –3, x1 = x2 = 3
B. m = –3, x1 = x2 = –3
C. m = 3, x1 = x2 = 3
D. m = 3, x1 = x2 = –3
Theo dõi (0) 2 Trả lời -


Phương trình \(\left( {m + 1} \right){x^2} - 2mx + m - 2 = 0\) vô nghiệm khi:
bởi Van Dung
 21/01/2021
21/01/2021
A. m ≤ -2
B. m < -2
C. m > 2
D. m ≥ 2
Theo dõi (0) 2 Trả lời -


A. m ∈ ∅
B. m = 0
C. m ∈ R
D. m ≠ 0
Theo dõi (0) 2 Trả lời -


Để phương trình \(m{x^2} + 2\left( {m--3} \right)x + m--5 = 0\) vô nghiệm, với giá trị của m là:
bởi Thùy Trang
 22/01/2021
22/01/2021
A. m > 9
B. m ≥ 9
C. m < 9
D. m < 9 và m ≠ 0
Theo dõi (0) 1 Trả lời -


A. m > 0
B. m < 0
C. m ≤ 0
D. m ≥ 0
Theo dõi (0) 2 Trả lời -


Tìm m để f(x) có tập nghiệm S=2?
bởi ohsehun
 25/08/2020
25/08/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Đường thẳng d cắt AB tại M thì tọa độ điểm M là?
bởi Hữu Thắng
 29/06/2020
Câu 5 ạ
29/06/2020
Câu 5 ạ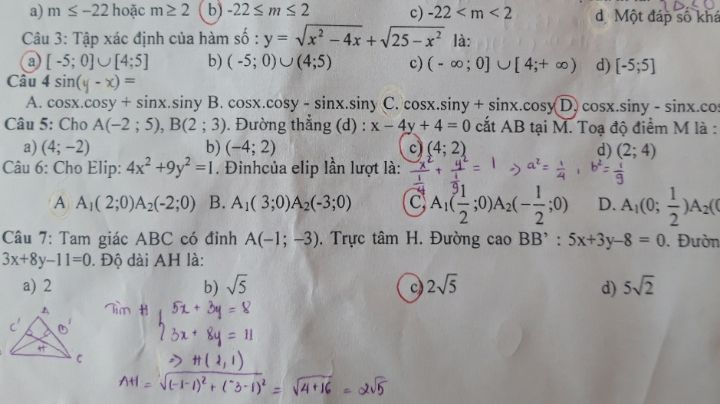 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tính \(\sin \alpha \)?
bởi Ngốc Nhỏ
 31/05/2020
31/05/2020
Giải giúp ik 1 câu cũng được
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để các bất phương trình sau nghiệm đúng với mọi x
bởi kim yo i
 27/04/2020
Tìm m để các bất phương trình sau nghiệm đúng với mọi x:
27/04/2020
Tìm m để các bất phương trình sau nghiệm đúng với mọi x: Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 12 trang 71 SGK Đại số 10
Bài tập 13 trang 71 SGK Đại số 10
Bài tập 3.40 trang 76 SBT Toán 10
Bài tập 3.41 trang 76 SBT Toán 10
Bài tập 3.42 trang 76 SBT Toán 10
Bài tập 3.43 trang 76 SBT Toán 10
Bài tập 3.44 trang 77 SBT Toán 10
Bài tập 3.45 trang 77 SBT Toán 10
Bài tập 3.46 trang 77 SBT Toán 10
Bài tập 3.47 trang 77 SBT Hình 10
Bài tập 3.48 trang 77 SBT Toán 10
Bài tập 3.49 trang 77 SBT Toán 10
Bài tập 3.50 trang 77 SBT Toán 10
Bài tập 3.51 trang 77 SBT Toán 10
Bài tập 3.52 trang 77 SBT Toán 10
Bài tập 3.53 trang 78 SBT Toán 10
Bài tập 50 trang 101 SGK Toán 10 NC
Bài tập 51 trang 101 SGK Toán 10 NC
Bài tập 52 trang 101 SGK Toán 10 NC
Bài tập 53 trang 101 SGK Toán 10 NC
Bài tập 54 trang 101 SGK Toán 10 NC
Bài tập 55 trang 101 SGK Toán 10 NC
Bài tập 56 trang 101 SGK Toán 10 NC
Bài tập 57 trang 101 SGK Toán 10 NC
Bài tập 58 trang 102 SGK Toán 10 NC
Bài tập 59 trang 102 SGK Toán 10 NC
Bài tập 60 trang 102 SGK Toán 10 NC
Bài tập 61 trang 102 SGK Toán 10 NC
Bài tập 62 trang 102 SGK Toán 10 NC






