Giải bài 3.40 tr 76 SBT Toán 10
Xác định m để mỗi cặp phương trình sau tương đương:
a) 3x - 1 = 0 và \(\frac{{3mx + 1}}{{x - 2}} + 2m - 1 = 0\)
b) \({x^2} + 3x - 4 = 0\) và \(m{x^2} - 4x - m + 4 = 0\)
Hướng dẫn giải chi tiết
a) 3x - 1 = 0 ⇔ x = \(\frac{1}{3}\)
Suy ra x = \(\frac{1}{3}\) là nghiệm của phương trình \(\frac{{3mx + 1}}{{x - 2}} + 2m - 1 = 0\)
\( \Rightarrow \frac{{3m.\frac{1}{3} + 1}}{{\frac{1}{3} - 2}} + 2m - 1 = 0 \Leftrightarrow m = \frac{8}{7}\)
b) Ta có \({x^2} + 3x - 4 = 0 \Leftrightarrow \left\{ \begin{array}{l}
x = 1\\
x = - 4
\end{array} \right.\)
Suy ra x = 1 và x = -4 là nghiệm của phương trình mx2 - 4x - m + 4 = 0
\( \Rightarrow \left\{ \begin{array}{l}
m{.1^2} - 4.1 - m + 4 = 0\\
m.{\left( { - 4} \right)^2} - 4.\left( { - 4} \right) - m + 4 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\forall m\\
m = - \frac{4}{3}
\end{array} \right. \Leftrightarrow m = - \frac{4}{3}\)
-- Mod Toán 10 HỌC247
-


Giải hệ phương trình x^2+y^2+3.căn(1-x^2)=1-3y và 2x.căn(x+2)+(x-1+y).căn(3+2y)=0
bởi Thanh Hoang Huynh
 16/04/2020
Giải hệ phương trình
16/04/2020
Giải hệ phương trình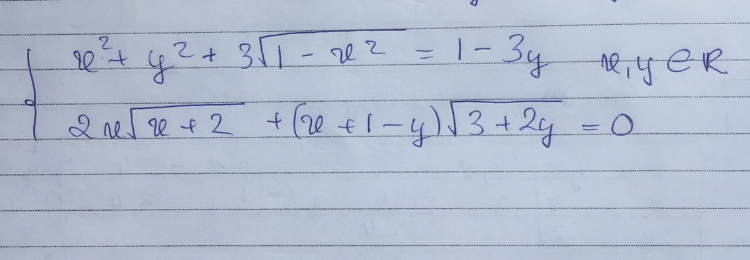 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x để đa thức f(x)=|x+1|/(x+2)-1 luôn âm
bởi Bích Vũ
 13/04/2020
13/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình |3x-2|=2x+3
bởi Hao Pham
 11/04/2020
11/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -

 Giúp e với e cần gấp
Giúp e với e cần gấp Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm tập xác định của hàm số y=căn(3x+6)+căn(4-x)
bởi Minh Anh
 01/04/2020
Mn giải giúp mình với ạ
01/04/2020
Mn giải giúp mình với ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để hệ bất phương trình x^2-2x+1<=0 và x^2-(2m+1)x+m^2+m<=0 có nghiệm.
bởi Nguyễn Linh
 19/03/2020
làm ơn giúp mình giải bài này
19/03/2020
làm ơn giúp mình giải bài này Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải bất phương trình x^2≤|1-2/x^2 |
bởi bùi thị ánh vân
 14/03/2020
14/03/2020
Giải bpt chứa trị
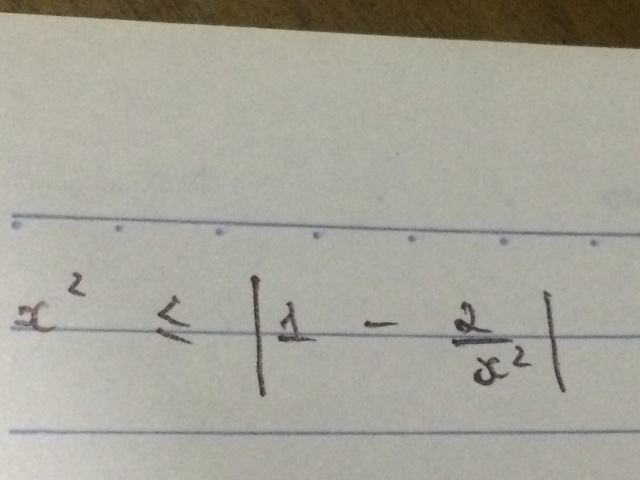 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Phương trình x^4-2(m^2+2)+5m^2+3=0 có các nghiệm là X1, X2,X3,X4. Tính theo m giá trị của biểu thức: M=1/X1^2+ 1/X2^2+ 1/X3^2+ 1/X4^2
bởi Nguyen Nguyen
 13/03/2020
Giúp mk vs!!!
13/03/2020
Giúp mk vs!!!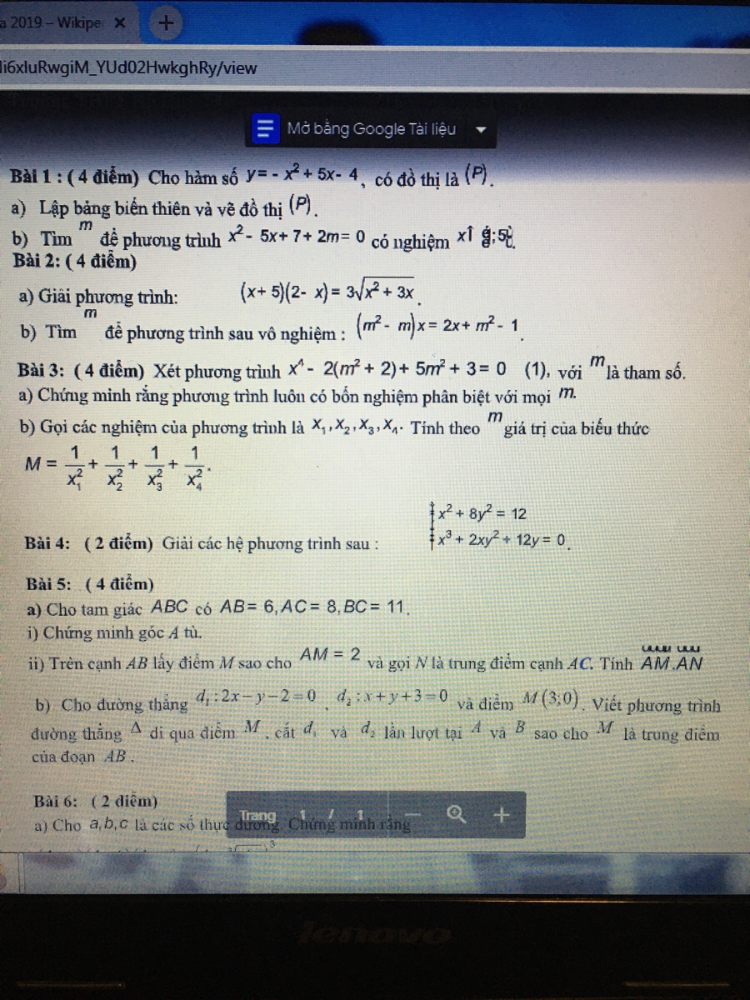 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


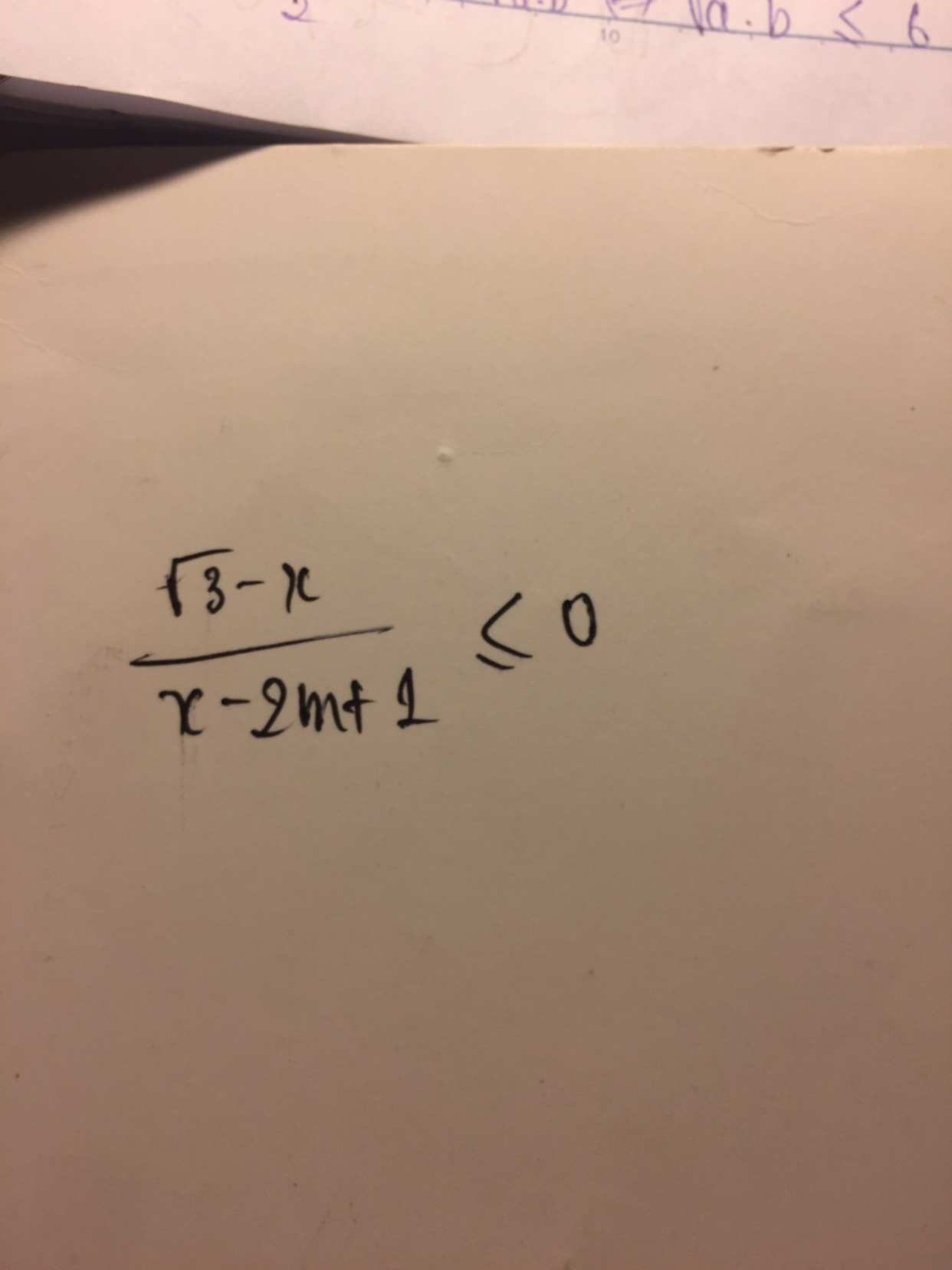 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Có bao nhiêu số tự nhiên có 4 chữ số và chia hết cho ít nhất một trong ba số 3, 4, 5?
bởi Lê Đạt
 01/03/2020
Có bao nhiêu số tự nhiên có 4 chữ số và chia hết cho ít nhất một trong ba số 3, 4, 5
01/03/2020
Có bao nhiêu số tự nhiên có 4 chữ số và chia hết cho ít nhất một trong ba số 3, 4, 5 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


 các bn giúp mk câu này nhé !Theo dõi (0) 0 Trả lời
các bn giúp mk câu này nhé !Theo dõi (0) 0 Trả lời -


Tìm GTLN của Q=2x+x^2 -x^4
bởi Gia Lộc La
 26/02/2020
26/02/2020
Tìm GTLN của Q=2x+x2 -x4
Theo dõi (0) 0 Trả lời -

 Tìm giá trị của m để pt vô nghiệm
Tìm giá trị của m để pt vô nghiệm Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải bất phương trình |4x-1|+|2-x| > x-2
bởi Minh Đức
 21/02/2020
21/02/2020
Mọi người giải câu này giúp mìn với
|4x-1|+|2-x|> x-2
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình (m-1)x+1-m^2=0 có nghiệm âm
bởi Trần Kim Thùy
 20/02/2020
20/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


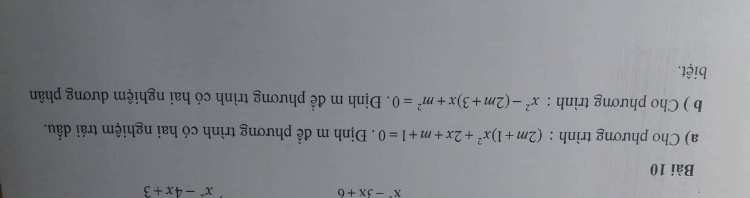 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm thời gian mà mỗi người làm một mình xong công việc biết cả hai người cùng làm thì 3h36p xong công việc đó
bởi Thư Lý
 18/02/2020
Toán 9
18/02/2020
Toán 9 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình x+căn(x+1/2+căn(x+1/4))=2
bởi Tồn Tại
 11/02/2020
11/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (x-3)căn(1+x)-x căn(4-x)=2x^2-6x-3
bởi Mai Khánh
 08/02/2020
08/02/2020
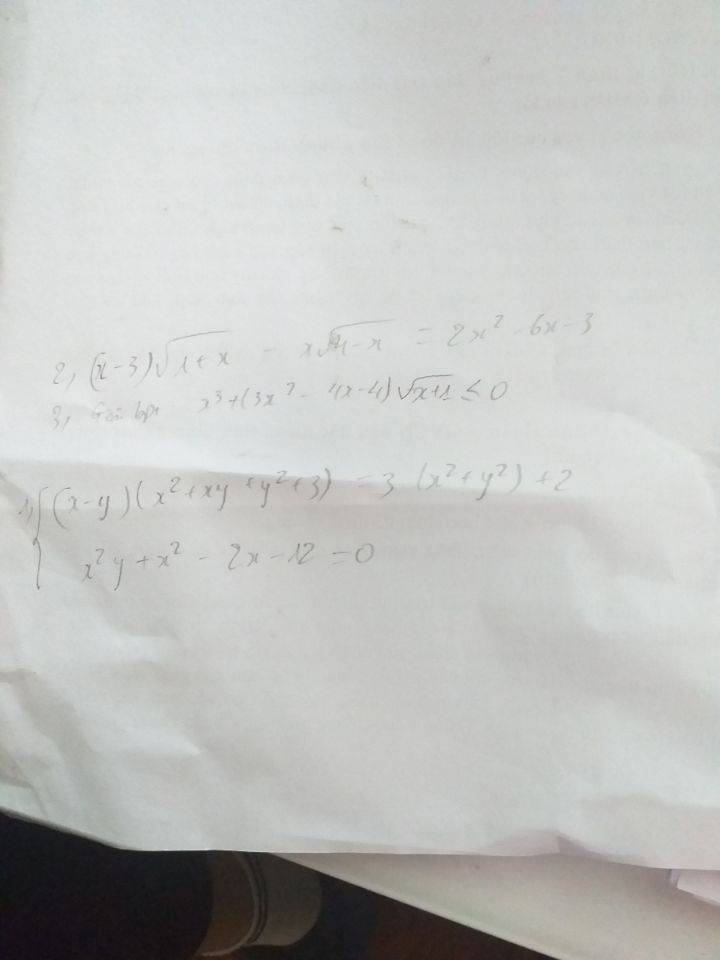 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây ?
bởi vũ thị ngọc ánh
 04/02/2020
04/02/2020
câu 14. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB =70m, phương nhìn AC tạo với phương nằm ngang góc 030, phương nhìn BC tạo với phương nằm ngang góc 015 30'. Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây ?
A. 135m.
B. 234m.
C. 165m
D. 195m.
Theo dõi (0) 0 Trả lời -

 Cho em hỏi câu 35 lm kiểu gì ạ
Cho em hỏi câu 35 lm kiểu gì ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 13 trang 71 SGK Đại số 10
Bài tập 3.39 trang 76 SBT Toán 10
Bài tập 3.41 trang 76 SBT Toán 10
Bài tập 3.42 trang 76 SBT Toán 10
Bài tập 3.43 trang 76 SBT Toán 10
Bài tập 3.44 trang 77 SBT Toán 10
Bài tập 3.45 trang 77 SBT Toán 10
Bài tập 3.46 trang 77 SBT Toán 10
Bài tập 3.47 trang 77 SBT Hình 10
Bài tập 3.48 trang 77 SBT Toán 10
Bài tập 3.49 trang 77 SBT Toán 10
Bài tập 3.50 trang 77 SBT Toán 10
Bài tập 3.51 trang 77 SBT Toán 10
Bài tập 3.52 trang 77 SBT Toán 10
Bài tập 3.53 trang 78 SBT Toán 10
Bài tập 50 trang 101 SGK Toán 10 NC
Bài tập 51 trang 101 SGK Toán 10 NC
Bài tập 52 trang 101 SGK Toán 10 NC
Bài tập 53 trang 101 SGK Toán 10 NC
Bài tập 54 trang 101 SGK Toán 10 NC
Bài tập 55 trang 101 SGK Toán 10 NC
Bài tập 56 trang 101 SGK Toán 10 NC
Bài tập 57 trang 101 SGK Toán 10 NC
Bài tập 58 trang 102 SGK Toán 10 NC
Bài tập 59 trang 102 SGK Toán 10 NC
Bài tập 60 trang 102 SGK Toán 10 NC
Bài tập 61 trang 102 SGK Toán 10 NC
Bài tập 62 trang 102 SGK Toán 10 NC





