Bài tập 59 trang 102 SGK Toán 10 NC
Cho các phương trình:
x2 + 3x − m + 1 = 0 (1) và
2x2 − x + 1 − 2p = 0 (2)
a) Biện luận số nghiệm của mỗi phương trình bằng đồ thị.
b) Kiểm tra lại kết quả trên bằng phép tính.
Hướng dẫn giải chi tiết
* Xét phương trình \({x^2} + {\rm{ }}3x{\rm{ }}-{\rm{ }}m{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\)
Ta có: (1) \( \Leftrightarrow {\rm{ }}{x^2} + {\rm{ }}3x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}m{\rm{ }}\)
Gọi (d) là đường thẳng \(y = m\).
Đồ thị hàm số \(y = x^2+ 3x + 1\) là parabol (P) có đỉnh là điểm \((-1,5; -1,25)\) và hướng bề lõm lên trên.
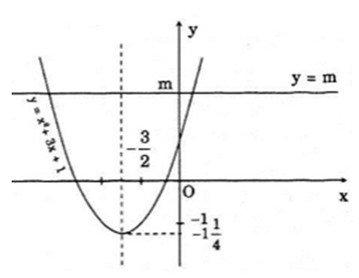
Do đó:
+ Khi \(m < -1, 25\) thì (d) không cắt (P), phương trình vô nghiệm.
+ Khi \(m = -1,25\) thì (d) và (P) có một điểm chung, phương trình có một nghiệm.
+ Khi \(m > -1,25\) thì (d) cắt (P) tại hai điểm. Phương trình có hai nghiệm phân biệt.
* Xét phương trình \(2x^2- x + 1 – 2p = 0\) (2)
(2) \(⇔ 2x^2 – x + 1 = 2p\)
Gọi (d) là đường thẳng \(y = 2p\); (P) là parabol \(y = 2x^2– x + 1 \)
Parabol (P) có đỉnh tại điểm: \(({1 \over 4};\,{7 \over 8})\) và hướng bề lõm lên trên.
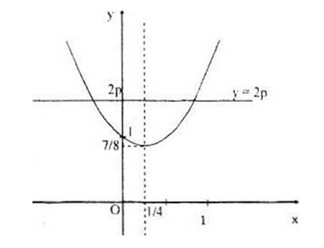
Do đó:
+ Nếu \(2p < {7 \over 8}\) , tức là \(p < {7 \over {16}}\) thì (d) không cắt (P), phương trình vô nghiệm.
+ Nếu \(2p = {7 \over 8}\) , tức là \(p = {7 \over {16}}\) thì (d) và (P) có một điểm chung, phương trình có một nghiệm.
+ Nếu \(2p > {7 \over 8}\) , tức là \(p > {7 \over {16}}\) thì (d) cắt (P) tại hai điểm chung, phương trình có hai nghiệm.
b)
Xét phương trình (1) có : \({\Delta _1}\) = 9 + 4m – 4 = 4m + 5
- Nếu 4m + 5 < 0 ⇔ m < -5/4 = -11/4 thì (1) vô nghiệm
- Nếu 4m + 5 = 0 ⇔ m = -11/4 thì (1) có nghiệm kép
- Nếu 4m + 5 > 0 ⇔ m > -11/4 thì (1) có hai nghiệm phân biệt
Rõ ràng kết quả biện luận bằng đồ thị số nghiệm của (1) và kết quả biện luận số nghiệm của (1) bằng phép tính là như nhau.
Xét phương trình :
2x2 – x + 1 – 2p = 0, có \({\Delta _2}\) = 1 – 8 + 16p = 16p - 7
- Nếu 16p – 7 < 0 ⇔ p < 7/16 thì (2) vô nghiệm
- Nếu 16p – 7 = 0 ⇔ p = 7/16 thì (2) có nghiệm kép x = 1/4
- Nếu 16p – 7 > 0 ⇔ p > 7/16 thì (2) có hai nghiệm phân biệt
Ta thấy kết quả biện luận số nghiệm bằng đồ thị và kết quả biện luận số nghiệm của (2) bằng phép tính là như nhau.
-- Mod Toán 10 HỌC247
-


Giải pt x^2+2x+căn(x-1)=1000/x+căn(19-x)+20
bởi hi hi
 06/11/2018
06/11/2018
Giải phương trình
\(x^2+2x+\sqrt{x-1}=\frac{1000}{x}+\sqrt{19-x}+20\)
Theo dõi (0) 1 Trả lời -


Cho phương trinh
\(\sqrt{1+x}+\sqrt{8-x}+\sqrt{\left(1+x\right)\left(8-x\right)}=a\)
a) Giải phương trình với a=3
b) Tìm a để phương trình có nghiệm
Theo dõi (0) 1 Trả lời -


Giải phương trình 1/căn(1-x^2)=căn 2+1/x
bởi minh thuận
 07/11/2018
07/11/2018
Giải giúp mk vs
\(\frac{1}{\sqrt{1-x^2}}=\sqrt{2}+\frac{1}{x}\)
Theo dõi (0) 2 Trả lời -


Giải hệ pt 8x^2y^3+27=18y^3 và 4x^2y+6x=y^2
bởi My Hien
 07/11/2018
07/11/2018
Giải hệ
\(8x^3y^3+27=18y^3\)
\(4x^2y+6x=y^2\)
Theo dõi (0) 2 Trả lời -


Giải hệ pt 6x^2-xy-2y^2=56 và 5x^2-xy-y^2=49
bởi Nguyen Ngoc
 07/11/2018
07/11/2018
Giải hệ
\(6x^2-xy-2y^2=56\)
\(5x^2-xy-y^2=49\)
Theo dõi (0) 2 Trả lời -


Giải hệ pt x^3-8x=y^3+2y và x^2-3=3(y^2+1)
bởi Huong Duong
 07/11/2018
07/11/2018
Giải hệ
\(x^3-8x=y^3+2y\)
\(x^2-3=3\left(y^2+1\right)\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 1/căn(1-x^2)=căn 2+1/x
bởi Nguyễn Hoài Thương
 07/11/2018
07/11/2018
giải pt
\(\frac{1}{\sqrt{1-x^2}}=\sqrt{2}+\frac{1}{x}\)
Theo dõi (0) 2 Trả lời -


Giải hệ 2 phương trình
\(\frac{x^2\left(x^2+2\right)+1}{y^2}+\left(x+y\right)^2=10\)
\(\left(x^2+1\right)+y\left(x+y\right)=4y\)
Theo dõi (0) 1 Trả lời -


Giải phương trình (4-x)/(x-5)=1/(1-x)
bởi Lê Minh Trí
 07/11/2018
07/11/2018
Giải phương trình
\(\frac{4-x}{x-5}=\frac{1}{1-x}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình x^3-6x^2+11x-6=0
bởi Nguyễn Thị Thu Huệ
 07/11/2018
07/11/2018
Giải phương trình sau
\(x^3-6x^2+11x-6=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2+|2x+1|-2=0
bởi Nhat nheo
 07/11/2018
07/11/2018
Giải phương trình sau :
\(^{x^2+\left|2x+1\right|-2=0}\)
Theo dõi (0) 1 Trả lời -


Biện luận theo a số nghiệm pt ax^3-(a+2)x^2+3x-1=0
bởi bala bala
 07/11/2018
07/11/2018
Biện luận theo a số nghiệm và viết biểu thức nghiệm của phương trình sau :
\(ax^3-\left(a+2\right)x^2+3x-1=0\)
Theo dõi (0) 1 Trả lời -


Giải và biện luận pt (x^2+2x-m)/(x-1)=0
bởi Lê Nhi
 07/11/2018
07/11/2018
Giải và biện luận phương trình sau :
\(\frac{x^2+2x-m}{x-1}=0\)
Theo dõi (0) 1 Trả lời -


Giải và biện luận pt (x-3)/(m-1)=1/(x+1)
bởi hi hi
 07/11/2018
07/11/2018
Giải và biện luận phương trình sau :
\(\frac{x-3}{m-1}=\frac{1}{x+1}\)
Theo dõi (0) 1 Trả lời -


Giải và biện luận pt mx^2-3x=x^2+1
bởi Kim Ngan
 07/11/2018
07/11/2018
Giải và biện luận phương trình sau :
\(mx^2-3x=x^2+1\)
Theo dõi (0) 1 Trả lời -


Giải pt căn bậc ba của (x+6) + x^2 = 7 - căn (x-1)
bởi Huong Duong
 22/10/2018
22/10/2018
\(\sqrt[3]{x+6}+x^2=7-\sqrt{x-1}\)
căn bậc ba của (x+6) + x2 = 7 - căn bậc hai của (x-1)
Theo dõi (0) 1 Trả lời -


Giải phương trình (1+x căn(x^2+1))(căn(x^2+1)-x)=1
bởi Hoa Hong
 07/11/2018
07/11/2018
Giải phương trình: \(\left(1+x\sqrt{x^2+1}\right)\left(\sqrt{x^2+1}-x\right)=1\)
Theo dõi (0) 2 Trả lời -


Giải pt 2x+căn(2x+1)=căn(x+3)+căn(1+căn(x+3))
bởi Lê Nguyễn Hạ Anh
 22/10/2018
22/10/2018
Giải pt:
\(2x+\sqrt{2x+1}=\sqrt{x+3}+\sqrt{1+\sqrt{x+3}}\)
Theo dõi (0) 1 Trả lời -


giải phương trình : a) \(\sqrt{3-x+x^2}\) + \(\sqrt{2+x-x^2}\) = 1 ; b) \(\sqrt{x+2+2\sqrt{x+1}}\) + \(\sqrt{x+2-2\sqrt{x+1}}\) = 2
Theo dõi (0) 1 Trả lời -


tìm m để đồ thị hàm số y = x2 + 2( m - 1 )x + m + 4m - 3 cắt Ox tại 2 điểm phân biệt có hoành độ x1 , x2 mà x1 = x2 + 2
Theo dõi (0) 1 Trả lời -


Giải hệ pt căn(x+3)=2 căn(y-1) và căn(y+1)=4-căn(x+3)
bởi Anh Trần
 06/11/2018
06/11/2018
giải các hệ phương trình : a) \(\sqrt{x+3}\) = 2\(\sqrt{y-1}\) + 2 và \(\sqrt{y+1}\) = 4 - \(\sqrt{x+3}\) ; b) x2 - xy = 3y và y2 - yx = 3x
Theo dõi (0) 1 Trả lời -


Giải và biện luận pt (2x+m-4)(2mx-x+m) =0
bởi Anh Trần
 07/11/2018
07/11/2018
giải và biện luận các phương trình sau: a) (2x+m-4)(2mx-x+m) =0 ; b) (m+1)x +m-2/x+3 =m
Theo dõi (0) 1 Trả lời -


Giải phương trình căn(x^2+3x+12)=x^2+3x
bởi Nguyễn Thị An
 07/11/2018
07/11/2018
giải phương trình sau : \(\sqrt{x^2+3x+12}\) = x2+3x
Theo dõi (0) 1 Trả lời





