Giải bài 1 tr 106 sách GK Toán Đại số 10
Sử dụng bất đẳng thức để viết các mệnh đề sau
a) x là số dương.
b) y là số không âm.
c) Với mọi số thực α, |α| là số không âm.
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng.
Hướng dẫn giải chi tiết
a) x > 0
b) y ≥ 0
c) ∀α ∈ R, |α| ≥ 0
d) ∀a, b > 0, \(\frac{{a + b}}{2} \ge \sqrt {ab} \)
-- Mod Toán 10 HỌC247
-
Tìm giá trị a và b để bất phương trình \((x - 2a + b - 1)(x + a - 2b + 1) \le 0\). Có tập nghiệm là đoạn [0;2].
bởi Nguyễn Thị An
26/04/2022
Theo dõi (0) 1 Trả lời -
Em hãy giải và biện luận bất phương trình sau theo tham số m: \((m - 1).\sqrt x \le 0\)
bởi sap sua
25/04/2022
Theo dõi (0) 1 Trả lời -
Thực hiện chứng minh rằng: \((a + 1)(b + 1)(a + c)(b + c) \ge 16abc\), với a, b, c là những số dương tùy ý.
bởi Lam Van
25/04/2022
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời -
Thực hiện chứng minh rằng: \({({x^2} - {y^2})^2} \ge 4xy{(x - y)^2},\forall x,y.\)
bởi lê Phương
26/04/2022
Theo dõi (0) 1 Trả lời -
Cho hình chữ nhật ABCD . AB = 4, AD = 3. Khi đó |AD+AB| bằng
Theo dõi (0) 1 Trả lời -
Xác định miền nghiệm của bất phương trình \( - x + 2 + 2\left( {y - 2} \right) < 2\left( {1 - x} \right)\) là nửa mặt phẳng không chứa điểm nào trong các điểm sau?
bởi Nguyễn Thủy Tiên
16/07/2021
A. \(\left( {1;\,\,1} \right)\) B. \(\left( {4;\,\,2} \right)\)
C. \(\left( {0;\,\,0} \right)\) D. \(\left( {1;\,\, - 1} \right)\)
Theo dõi (0) 1 Trả lời -
Giải bất phương trình: (x^2-6x 9) (4-x) >0
bởi Khoa Huỳnh
20/04/2021
Theo dõi (0) 0 Trả lời -
Cho a, b là các số thực dương thỏa mãn a b nhỏ hơn hoặc bằng 1 . Tìm giá trị nhỏ nhất của biểu thức : A= 1/(1 a^2 b^2) + 1/2ab .
bởi Na Tra
31/03/2021
Cho a , b là các số thực dương thỏa mãn a b nhỏ hơn hoặc bằng 1 . Tìm giá trị nhỏ nhất của biểu thức : A= 1/(1 a^2 b^2) 1/2ab .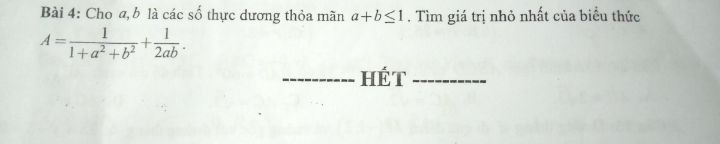
Theo dõi (0) 0 Trả lời -
Tập nghiệm của bất phương trình |3x-3| < x 5 có dạng [ a;b ]. Khi đó a b bằng
bởi Trần Ngọc Anh Thư
26/03/2021
A.7 B.4 C.12 D. 17/2Theo dõi (0) 0 Trả lời -
Tìm tất cả các giá trị của m để ứng với mỗi giá trị đó phương trình: \(\left| {1 - mx} \right| = 1 + \left( {1 - 2m} \right)x + m{x^2}\). Chỉ có đúng một nghiệm.
bởi Lê Minh Hải
22/02/2021
Theo dõi (0) 1 Trả lời -
Tùy thuộc vào giá trị của tham số m để ứng với mỗi giá trị đó phương trình: \(\left| {{x^2} - 2x - 3} \right| = m\).
bởi Tra xanh
21/02/2021
Theo dõi (0) 1 Trả lời -
Cho phương trình \(\left( {m\sqrt 5 } \right){x^2} - 3mx + m + 1 = 0.\) Với các giá trị nào của m thì phương trình đã cho có nghiệm?
bởi Nguyễn Trà Long
22/02/2021
Theo dõi (0) 1 Trả lời -
Giải bất phương trình sau: \(\dfrac{9}{{\left| {x - 5} \right| - 3}} \ge \left| {x - 2} \right|\)
bởi Nguyen Phuc
21/02/2021
Theo dõi (0) 1 Trả lời -
Giải bất phương trình sau: \(\dfrac{3}{{\left| {x + 3} \right| - 1}} \ge \left| {x + 2} \right|\)
bởi Lê Tường Vy
21/02/2021
Theo dõi (0) 1 Trả lời -
Giải bất phương trình: \(\sqrt {x - \dfrac{1}{x}} - \sqrt {1 - \dfrac{1}{x}} > \dfrac{{x - 1}}{x}\)
bởi Minh Hanh
22/02/2021
Theo dõi (0) 1 Trả lời -
Xét dấu biểu thức sau: \(\dfrac{{{x^4} - 17{x^2} + 60}}{{x\left( {{x^2} - 8x + 5} \right)}}\)
bởi Thùy Trang
22/02/2021
Theo dõi (0) 1 Trả lời -
Xét dấu biểu thức sau: \(\dfrac{{15{x^2} - 7x - 2}}{{6{x^2} - x + 5}}\)
bởi Mai Bảo Khánh
21/02/2021
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời
-
Theo dõi (0) 1 Trả lời
-
Tùy theo giá trị của tham số m, hãy biện luận số nghiệm phương trình: \(\left( {m + 3} \right){x^4} - \left( {2m - 1} \right){x^2} - 3 = 0\).
bởi Phan Thị Trinh
22/02/2021
Theo dõi (0) 1 Trả lời -
Xác định các giá trị của tham số m để bất phương trình sau nghiệm đúng với mọi x: \(\dfrac{{{x^2} + mx - 1}}{{2{x^2} - 2x + 3}} < 1\).
bởi thu hằng
21/02/2021
Theo dõi (0) 1 Trả lời -
Giải và biện luận bất phương trình sau theo tham số m: \(\left( {m - 3} \right){x^2} - 2\left( {m + 1} \right)x - \left( {2m - 3} \right) \le 0\)
bởi Thụy Mây
22/02/2021
Theo dõi (0) 1 Trả lời -
Giải và biện luận bất phương trình sau theo tham số m: \(m{x^2} + 4x + 1 \le 0\)
bởi Ban Mai
21/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 106 SGK Đại số 10
Bài tập 3 trang 106 SGK Đại số 10
Bài tập 4 trang 106 SGK Đại số 10
Bài tập 5 trang 106 SGK Đại số 10
Bài tập 6 trang 106 SGK Đại số 10
Bài tập 7 trang 106 SGK Đại số 10
Bài tập 8 trang 107 SGK Đại số 10
Bài tập 9 trang 107 SGK Đại số 10
Bài tập 10 trang 107 SGK Đại số 10
Bài tập 11 trang 107 SGK Đại số 10
Bài tập 12 trang 107 SGK Đại số 10
Bài tập 13 trang 107 SGK Đại số 10
Bài tập 14 trang 107 SGK Đại số 10
Bài tập 15 trang 108 SGK Đại số 10
Bài tập 16 trang 108 SGK Đại số 10
Bài tập 17 trang 108 SGK Đại số 10
Bài tập 4.76 trang 125 SBT Toán 10
Bài tập 4.77 trang 125 SBT Toán 10
Bài tập 4.78 trang 125 SBT Toán 10
Bài tập 4.79 trang 125 SBT Toán 10
Bài tập 4.80 trang 125 SBT Toán 10
Bài tập 4.81 trang 125 SBT Toán 10
Bài tập 4.82 trang 125 SBT Toán 10
Bài tập 4.83 trang 126 SBT Toán 10
Bài tập 4.84 trang 126 SBT Toán 10
Bài tập 76 trang 155 SGK Toán 10 NC
Bài tập 77 trang 155 SGK Toán 10 NC
Bài tập 78 trang 155 SGK Toán 10 NC
Bài tập 79 trang 155 SGK Toán 10 NC
Bài tập 80 trang 155 SGK Toán 10 NC
Bài tập 81 trang 155 SGK Toán 10 NC
Bài tập 82 trang 155 SGK Toán 10 NC
Bài tập 83 trang 156 SGK Toán 10 NC
Bài tập 84 trang 156 SGK Toán 10 NC
Bài tập 85 trang 156 SGK Toán 10 NC
Bài tập 86 trang 156 SGK Toán 10 NC
Bài tập 87 trang 156 SGK Toán 10 NC
