Giải bài 8 tr 107 sách GK Đại số 10
Nếu quy tắc biểu diễn hình học tập nghiệm của bất phương trình ax + by ≤ c.
Hướng dẫn giải chi tiết
- Vẽ đường thẳng (d): ax + by = c.
- Chọn điểmM(xo, yo) (thường chọn điểm (0; 0)) và tính giá trị axo + byo.
- So sánh axo + byo với c:
+ Nếu axo + byo < c thì miền nghiệm là nửa mặt phẳng bờ (d) chứa M.
+ Nếu axo + byo = c thì miền nghiệm là đường thẳng (d).
+ Nếu axo + byo > c thì miền nghiệm là nửa mặt phẳng bờ (d) không chứa M
-- Mod Toán 10 HỌC247
-


Tìm m để BPT đúng với mọi \(x>\dfrac {3}{2}\)?
bởi Hoàng Ngân
 31/05/2020
31/05/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Suy luận nào sau đây đúng?
bởi Nguyễn Sơn Ca
 30/05/2020
30/05/2020
A. \(\left\{ \begin{array}{l}
a > b\\
c > d
\end{array} \right. \Rightarrow ac > bd\).B. \(\left\{ \begin{array}{l}
a > b\\
c > d
\end{array} \right. \Rightarrow \frac{a}{c} > \frac{b}{d}\).C. \(\left\{ \begin{array}{l}
a > b\\
c > d
\end{array} \right. \Rightarrow a - c > b - d\).D. \(\left\{ \begin{array}{l}
a > b > 0\\
c > d > 0
\end{array} \right. \Rightarrow ac > bd\).Theo dõi (0) 1 Trả lời -


Trong các hình chữ nhật có cùng chu vi thì
bởi Trịnh Lan Trinh
 31/05/2020
31/05/2020
A. Hình vuông có diện tích nhỏ nhất.
B. Hình vuông có diện tích lớn nhất.
C. Không xác định được hình có diện tích lớn nhất.
D. Cả A, B, C đều sai.
Theo dõi (0) 1 Trả lời -


Cho ba số \(a; b; c\) thoả mãn đồng thời: \(a + b - c > 0;b + c - a > 0;c + a - b > 0\) Để ba số \(a, b, c\) là ba cạnh của một tam giác thì cần thêm đều kiện gì?
bởi Lê Gia Bảo
 31/05/2020
31/05/2020
A. Cần có cả \(a,b,c \ge 0\).
B. Cần có cả \(a,b,c > 0\)
C. Chỉ cần một trong ba số dương
D. Không cần thêm điều kiện gì.
Theo dõi (0) 1 Trả lời -


Cho biết hai số \(a\) và \(b\) có tổng bằng 3. Khi đó, tích hai số \(a\) và \(b\)
bởi Nguyễn Thanh Trà
 30/05/2020
30/05/2020
A. có giá trị nhỏ nhất là \(\frac{9}{4}\).
B. có giá trị lớn nhất là \(\frac{9}{4}\).
C. có giá trị lớn nhất là \(\frac{3}{2}\).
D. không có giá trị lớn nhất.
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f\left( x \right) = \frac{1}{{\sqrt {{x^2} + 1} }}\). Mệnh đề nào sau đây là đúng?
bởi Trần Bảo Việt
 30/05/2020
30/05/2020
A. \(f\left( x \right)\) có giá trị nhỏ nhất là 0, giá trị lớn nhất bằng 1.
B. \(f\left( x \right)\) không có giá trị nhỏ nhất, giá trị lớn nhất bằng 1.
C. \(f\left( x \right)\) có giá trị nhỏ nhất là 1, giá trị lớn nhất bằng 2.
D. \(f\left( x \right)\) không có giá trị nhỏ nhất và giá trị lớn nhất.
Theo dõi (0) 1 Trả lời -


Cho biểu thức \(f\left( x \right) = \sqrt {1 - {x^2}} \). Kết luận nào sau đây đúng?
bởi Trần Bảo Việt
 30/05/2020
30/05/2020
A. Hàm số \(f\left( x \right)\) chỉ có giá trị lớn nhất, không có giá trị nhỏ nhất.
B. Hàm số \(f\left( x \right)\) chỉ có giá trị nhỏ nhất, không có giá trị lớn nhất.
C. Hàm số \(f\left( x \right)\) có giá trị nhỏ nhất và giá trị lớn nhất.
D. Hàm số \(f\left( x \right)\) không có giá trị nhỏ nhất và không có giá trị lớn nhất.
Theo dõi (0) 1 Trả lời -


Giá trị nhỏ nhất của biểu thức \({x^2} + 3\left| x \right|\) với \(x \in R\)
bởi Nguyễn Lệ Diễm
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Cho bất đẳng thức \(\left| {a - b} \right| \le \left| a \right| + \left| b \right|\). Dấu đẳng thức xảy ra khi nào?
bởi Trần Bảo Việt
 31/05/2020
31/05/2020
A. \(a=b\). B. \(ab \le 0\).
C. \(ab \ge 0\). D. \(ab = 0\).
Theo dõi (0) 1 Trả lời -


Giải bất phương trình (x-2)(x+6)(2x+5)≤0
bởi Nguyễn Bảo
 27/05/2020
27/05/2020
(x-2)(x+6)(2x+5)≤0
Theo dõi (0) 0 Trả lời -


Tìm x biết |3x-2|>7
bởi Phạm Thị Quế Châu
 15/05/2020
Đề ôn tập KT thử
15/05/2020
Đề ôn tập KT thử Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để các hàm số xác định
bởi Thương Mân
 13/05/2020
13/05/2020
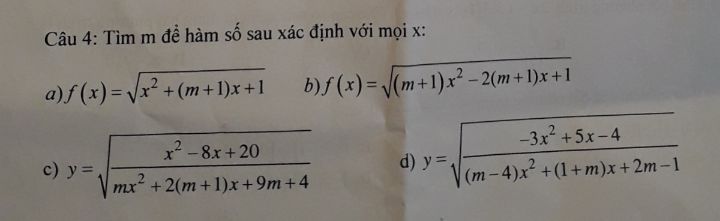 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm điểm C thuộc d sao cho tam giác ABC cân tại C?
bởi Phùng Lệ Quyên
 09/05/2020
...
09/05/2020
...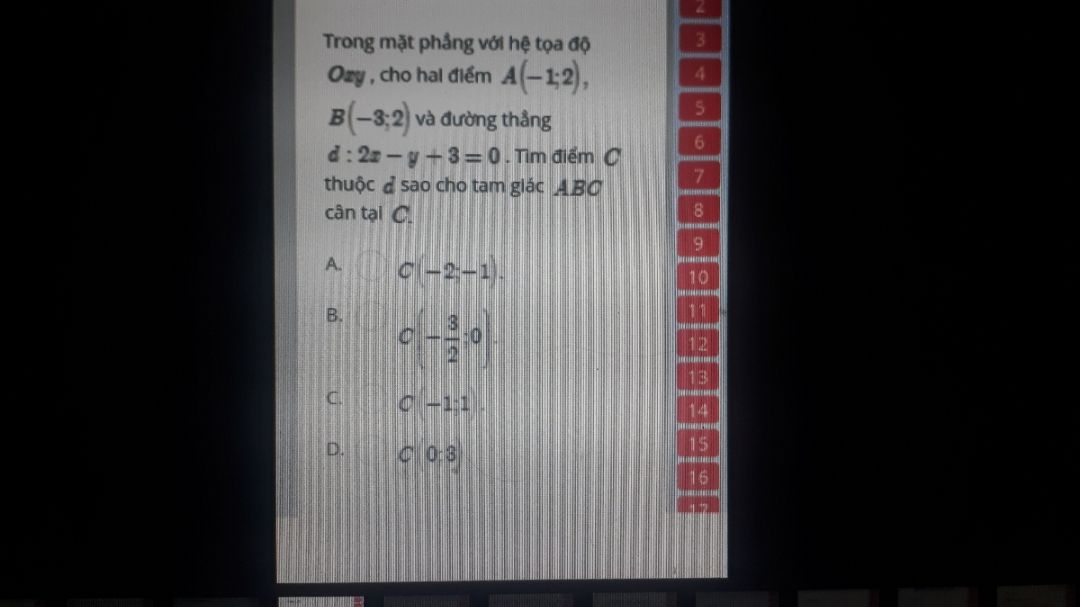 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để bpt x^2-x+m<=0 vô nghiệm
bởi Mai Anh
 03/05/2020
03/05/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


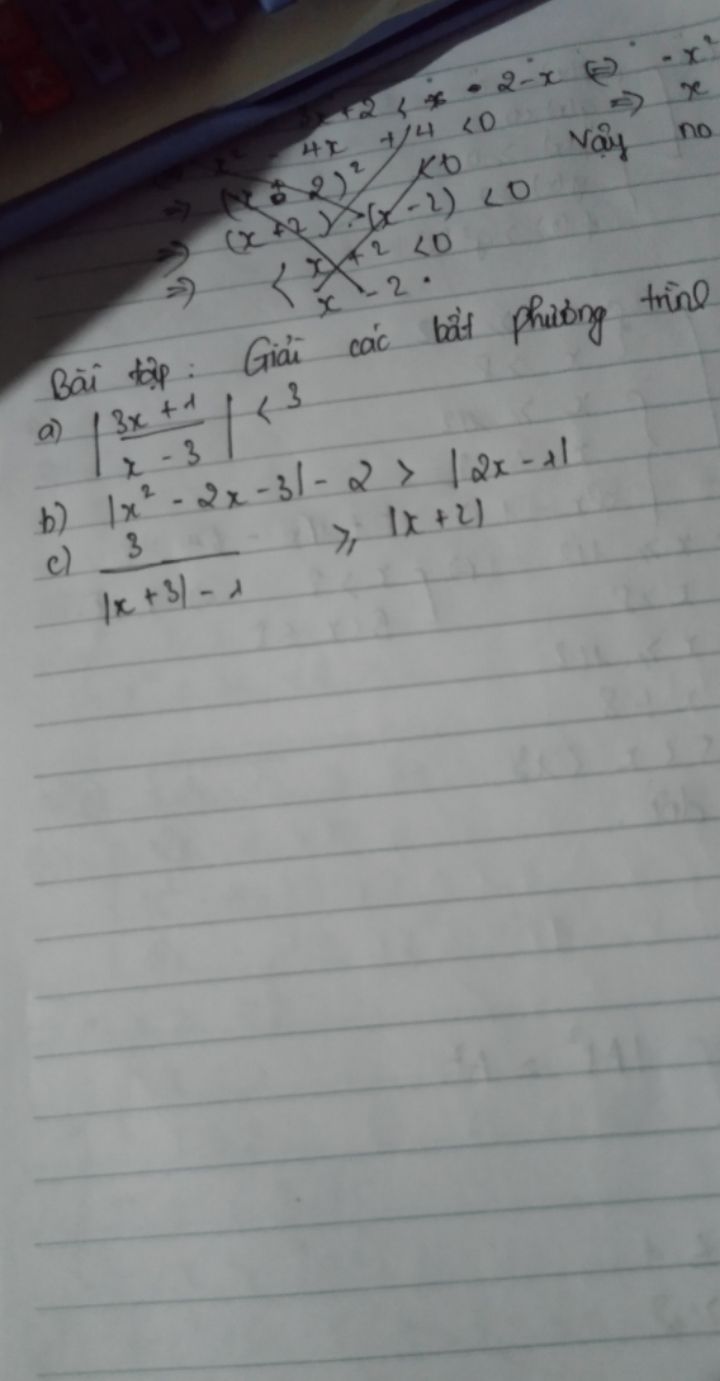 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải BPT \(\sqrt {{x^2} - 2x - 3} + x < 1\)?
bởi Thu Hà Võ
 30/04/2020
30/04/2020
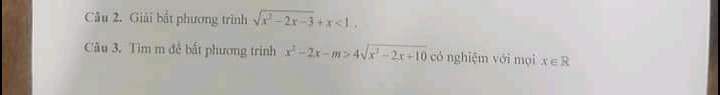 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bất phương trình x^2 + 2x - 8/|x + 1|
bởi Ngô Thị Cẩm Tú
 24/04/2020
24/04/2020
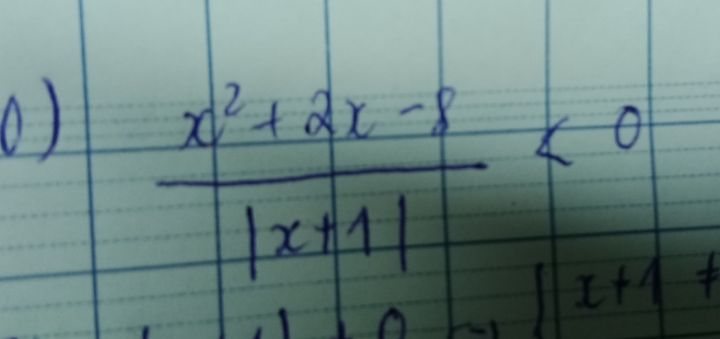 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải bất phương trình 2x-4 / căn ( x^2-3x-10)>1
bởi Minh Hang Vu
 24/04/2020
24/04/2020
Giải bất phương trình 2x-4 / căn ( x^2-3x-10)>1
Theo dõi (0) 0 Trả lời -


Chứng minh √a +√b +√c >= ab + bc + ac biết , b, c dương thỏa mãn a + b + c = 3
bởi CaoNgọc AnhQuân
 24/04/2020
24/04/2020
cho 3 số a, b, c dương thỏa mãn a + b + c = 3. chứng minh √a +√b +√c >= ab + bc + ac
Theo dõi (0) 0 Trả lời -


Giải bất phương trình x^3-9x/2-x>=0
bởi Thắm Nguyễn
 23/04/2020
23/04/2020
Giải bất phương trình x^3-9x/2-x>=0
Theo dõi (0) 2 Trả lời -


Tập nghiêm cua bất phương trình x-1<0/x+2
bởi Vy Thị Thu Hằng
 23/04/2020
Tim tập xác định giải bất phương trình bằng cách xét dấu tính phương trình đại và độ lệch chuẩn
23/04/2020
Tim tập xác định giải bất phương trình bằng cách xét dấu tính phương trình đại và độ lệch chuẩn Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tìm m để phương trình (m^2+1)x^2-3(m-3)x+m^2-5m+4=0 có 2 nghiệm trái dấu
Theo dõi (1) 5 Trả lời -


Tìm m để pt (m^2 +)x^2-3(m-3)x m^2-5m+4=0 có 2 nghiệm trái dấu
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 6 trang 106 SGK Đại số 10
Bài tập 7 trang 106 SGK Đại số 10
Bài tập 9 trang 107 SGK Đại số 10
Bài tập 10 trang 107 SGK Đại số 10
Bài tập 11 trang 107 SGK Đại số 10
Bài tập 12 trang 107 SGK Đại số 10
Bài tập 13 trang 107 SGK Đại số 10
Bài tập 14 trang 107 SGK Đại số 10
Bài tập 15 trang 108 SGK Đại số 10
Bài tập 16 trang 108 SGK Đại số 10
Bài tập 17 trang 108 SGK Đại số 10
Bài tập 4.76 trang 125 SBT Toán 10
Bài tập 4.77 trang 125 SBT Toán 10
Bài tập 4.78 trang 125 SBT Toán 10
Bài tập 4.79 trang 125 SBT Toán 10
Bài tập 4.80 trang 125 SBT Toán 10
Bài tập 4.81 trang 125 SBT Toán 10
Bài tập 4.82 trang 125 SBT Toán 10
Bài tập 4.83 trang 126 SBT Toán 10
Bài tập 4.84 trang 126 SBT Toán 10
Bài tập 76 trang 155 SGK Toán 10 NC
Bài tập 77 trang 155 SGK Toán 10 NC
Bài tập 78 trang 155 SGK Toán 10 NC
Bài tập 79 trang 155 SGK Toán 10 NC
Bài tập 80 trang 155 SGK Toán 10 NC
Bài tập 81 trang 155 SGK Toán 10 NC
Bài tập 82 trang 155 SGK Toán 10 NC
Bài tập 83 trang 156 SGK Toán 10 NC
Bài tập 84 trang 156 SGK Toán 10 NC
Bài tập 85 trang 156 SGK Toán 10 NC
Bài tập 86 trang 156 SGK Toán 10 NC
Bài tập 87 trang 156 SGK Toán 10 NC





