Giải bài 7 tr 106 sách GK Toán Đại số 10
Điều kiện của một bất phương trình là gì? Thế nào là hai bất phương trình tương đương.
Hướng dẫn giải chi tiết
- Điều kiện của một bất phương trình là các điều kiện của ẩn x sao cho các biểu thức của bất phương trình đó đều có nghĩa.
- Hai bất phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
-- Mod Toán 10 HỌC247
-


Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}\dfrac{{x - 1}}{2} < - x + 1\\\dfrac{{5 - 4x}}{2} \le 4\end{array} \right.\) là:
bởi Ngoc Han
 19/02/2021
19/02/2021
A. \(S = \left( { - \dfrac{3}{4};1} \right)\)
B. \(S = \left[ { - \dfrac{3}{4};1} \right]\)
C. \(S = \left( { - \dfrac{3}{4};1} \right]\)
D. \(S = \left[ { - \dfrac{3}{4};1} \right)\)
Theo dõi (0) 1 Trả lời -


Cho bất phương trình \(mx + 6 < 2x + 3m\) . Với m< 2 thì tập nghiệm của bất phương trình là:
bởi Hoa Lan
 18/02/2021
18/02/2021
A. \(S = \left( {3; + \infty } \right)\)
B. \(S = \left[ {3; + \infty } \right)\)
C. \(S = \left( { - \infty ;3} \right)\)
D. \(S = \left( { - \infty ;3} \right]\)
Theo dõi (0) 1 Trả lời -


Tập xác định của hàm số \(f\left( x \right) = \sqrt {\dfrac{{2 - x}}{{4 + x}}} \) là:
bởi het roi
 19/02/2021
19/02/2021
A. \(D = \left( { - 4;2} \right)\)
B. \(D = \left[ { - 4;2} \right]\)
C. \(D = \left[ { - 4;2} \right)\)
D. \(D = \left( { - 4;2} \right]\)
Theo dõi (0) 1 Trả lời -


Cho bất phương trình \(m\left( {x - m} \right) \ge x- 1\) . Các giá trị của m để bất phương trình có tập nghiệm \(S = \left( { - \infty ;m + 1} \right]\) là:
bởi thanh hằng
 19/02/2021
19/02/2021
A.\(m = 1\)
B.\(m < 1\)
C.\(m > 1\)
D.\(m \ge 1\)
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


(A) \(\left\{ \matrix{{x^2} - 2x \le 0 \hfill \cr 2x + 1 < 3x + 2 \hfill \cr} \right.\)
(B) \(\left\{ \matrix{{x^2} - 4 > 0 \hfill \cr {1 \over {x + 2}} < {1 \over {x + 1}} \hfill \cr} \right.\)
(C) \(\left\{ \matrix{{x^2} - 5x + 2 < 0 \hfill \cr {x^2} + 8x + 1 \le 0 \hfill \cr} \right.\)
(D) \(\left\{ \matrix{|x - 1| \le 2 \hfill \cr |2x + 1| \le 3 \hfill \cr} \right.\)
Theo dõi (0) 1 Trả lời -


(A). \(m=1\)
(B). \(m =3\)
(C). \(m = 0\)
(D). \(m=0,25\)
Theo dõi (0) 1 Trả lời -


Bất phương trình \((x+1) \sqrt x ≤ 0\) tương đương với bất phương trình nào trong các bất phương trình sau?
bởi Lê Chí Thiện
 19/02/2021
19/02/2021
(A). \(\sqrt {x{{(x + 1)}^2}} \le 0\)
(B). \((x+1) \sqrt x<0\)
(C). \((x+1)^2\sqrt x ≤ 0\)
(D). \((x+1)^2\sqrt x < 0\)
Theo dõi (0) 1 Trả lời -


Số \(-2\) thuộc tập nghiệm của bất phương trình nào trong các bất phương trình sau:
bởi Anh Nguyễn
 19/02/2021
19/02/2021
(A). \(2x +1 > 1 – x\)
(B). \((2x + 1) (1 - x) < x^2\)
(C). \({1 \over {1 - x}} + 2 \le 0\)
(D) \((2 - x) (x + 2)^2<0\)
Theo dõi (0) 1 Trả lời -


Cho \(a, b, c\) là độ dài ba cạnh của một tam giác. Sử dụng định lí về dấu của tam thức bậc hai , chứng minh rằng: \({b^2}{x^{2}}-{\rm{ }}({b^2} + {c^2}-{\rm{ }}{a^2})x{\rm{ }} + {c^2} > 0,{\rm{ }}\forall x.\)
bởi khanh nguyen
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Cho \(a>0, \, b>0\). Chứng minh rằng: \({a \over {\sqrt b }} + {b \over {\sqrt a }} \ge \sqrt a + \sqrt b.\)
bởi Aser Aser
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Phát biểu định lí về dấu của tam thức bậc hai.
bởi hi hi
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Nêu quy tắc biểu diễn hình học tập nghiệm của bất phương trình \(ax+by ≤ c.\)
bởi Lê Tấn Thanh
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Điều kiện của một bất phương trình là gì? Thế nào là hai bất phương trình tương đương?
bởi Nguyen Ngoc
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Cho \(a, b, c > 0\). Chứng minh rằng: \({{a + b} \over c} + {{b + c} \over a} + {{c + a} \over b} \ge 6.\)
bởi Phạm Phú Lộc Nữ
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Khi cân một vật với độ chính xác đến \(0,05kg\), người ta cho biết kết quả là \(P = 26,4kg\). Hãy chỉ ra khối lượng thực của vật đó nằm trong khoảng nào.
bởi Nguyễn Trà Giang
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Trong các suy luận đã cho sau, suy luận nào đúng?
bởi Phung Hung
 19/02/2021
19/02/2021
(A) \(\left\{ \matrix{x < 1 \hfill \cr y < 1 \hfill \cr} \right. ⇒ xy<1\)
(B) \(\left\{ \matrix{x < 1 \hfill \cr y < 1 \hfill \cr} \right.⇒ {x \over y} <1\)
(C) \(\left\{ \matrix{0 < x < 1 \hfill \cr y < 1 \hfill \cr} \right.⇒ xy<1\)
(D) \(\left\{ \matrix{x < 1 \hfill \cr y < 1 \hfill \cr} \right.⇒ x – y < 0.\)
Theo dõi (0) 1 Trả lời -


Giải bất phương trình
bởi Phương Trang
 03/02/2021
03/02/2021
Giải bất phương trình
Theo dõi (0) 0 Trả lời -


Tìm giá trị lớn nhất của P?
bởi Phạm Thủy
 18/07/2020
18/07/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tất cả các giá trị thực của tham số m để bất phương trình (m+ 1)x^2 + mx +m<0 đúng với mọi x thuộc R?
bởi Nguyen Ha Linh
 27/06/2020
Tìm giá trị thựcTheo dõi (0) 1 Trả lời
27/06/2020
Tìm giá trị thựcTheo dõi (0) 1 Trả lời -


Tìm m để phương trình x bình trừ 2x m 3=0 để có 2 nghiệm phân biệt
Theo dõi (0) 2 Trả lời -


Với giá trị nào của m thì BPT trên vô nghiệm?
bởi lâm diệp
 19/06/2020
19/06/2020
Mọi người giải giúp mk vs ạ mk sắp thi rồi mà chưa biết làm☹️
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để f(x) vô nghiệm?
bởi Thư Nguyễn Minh
 03/06/2020
03/06/2020
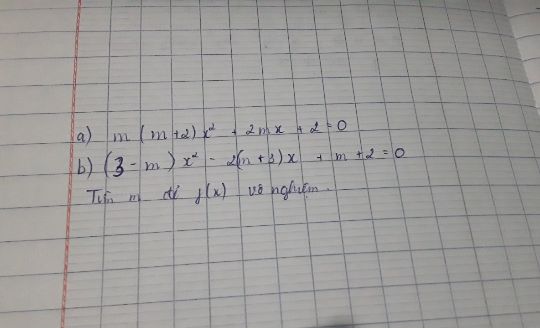 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Giải bất phương trình
Giải bất phương trình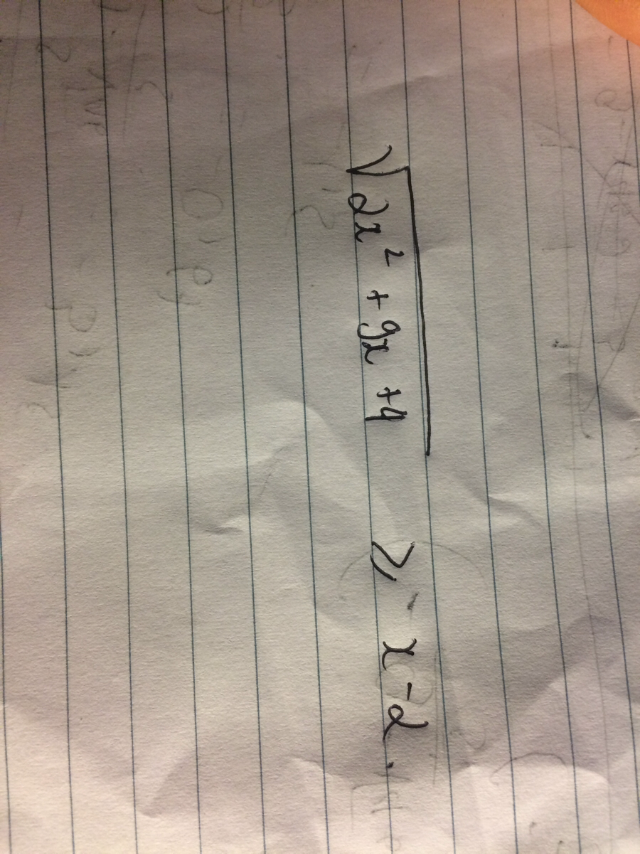 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 5 trang 106 SGK Đại số 10
Bài tập 6 trang 106 SGK Đại số 10
Bài tập 8 trang 107 SGK Đại số 10
Bài tập 9 trang 107 SGK Đại số 10
Bài tập 10 trang 107 SGK Đại số 10
Bài tập 11 trang 107 SGK Đại số 10
Bài tập 12 trang 107 SGK Đại số 10
Bài tập 13 trang 107 SGK Đại số 10
Bài tập 14 trang 107 SGK Đại số 10
Bài tập 15 trang 108 SGK Đại số 10
Bài tập 16 trang 108 SGK Đại số 10
Bài tập 17 trang 108 SGK Đại số 10
Bài tập 4.76 trang 125 SBT Toán 10
Bài tập 4.77 trang 125 SBT Toán 10
Bài tập 4.78 trang 125 SBT Toán 10
Bài tập 4.79 trang 125 SBT Toán 10
Bài tập 4.80 trang 125 SBT Toán 10
Bài tập 4.81 trang 125 SBT Toán 10
Bài tập 4.82 trang 125 SBT Toán 10
Bài tập 4.83 trang 126 SBT Toán 10
Bài tập 4.84 trang 126 SBT Toán 10
Bài tập 76 trang 155 SGK Toán 10 NC
Bài tập 77 trang 155 SGK Toán 10 NC
Bài tập 78 trang 155 SGK Toán 10 NC
Bài tập 79 trang 155 SGK Toán 10 NC
Bài tập 80 trang 155 SGK Toán 10 NC
Bài tập 81 trang 155 SGK Toán 10 NC
Bài tập 82 trang 155 SGK Toán 10 NC
Bài tập 83 trang 156 SGK Toán 10 NC
Bài tập 84 trang 156 SGK Toán 10 NC
Bài tập 85 trang 156 SGK Toán 10 NC
Bài tập 86 trang 156 SGK Toán 10 NC
Bài tập 87 trang 156 SGK Toán 10 NC





