Giải bài 10 tr 107 sách GK Toán Đại số 10
Cho a > 0, b > 0. Chứng minh rằng \(\frac{a}{{\sqrt b }} + \frac{b}{{\sqrt a }} \ge \sqrt a + \sqrt b \)
Hướng dẫn giải chi tiết
Ta có
\(\begin{array}{l}
\frac{a}{{\sqrt b }} + \frac{b}{{\sqrt a }} \ge \sqrt a + \sqrt b \\
\Leftrightarrow a\sqrt a + b\sqrt b \ge \sqrt a \sqrt b \left( {\sqrt a + \sqrt b } \right)\\
\Leftrightarrow \left( {\sqrt a + \sqrt b } \right)\left( {a + b - \sqrt a \sqrt b } \right) \ge \sqrt a \sqrt b \left( {\sqrt a + \sqrt b } \right)\\
\Leftrightarrow a + b - \sqrt a \sqrt b \ge \sqrt a \sqrt b \\
\Leftrightarrow \left( {{{\sqrt a }^2}} \right) + {\left( {\sqrt b } \right)^2} - 2\sqrt a \sqrt b \ge 0\\
\Leftrightarrow {\left( {\sqrt a - \sqrt b } \right)^2} \ge 0
\end{array}\)
(đúng với mọi a > 0, b > 0)
Do đó \(\frac{a}{{\sqrt b }} + \frac{b}{{\sqrt a }} \ge \sqrt a + \sqrt b \) (đpcm)
-- Mod Toán 10 HỌC247
-


Tìm GTNN của biểu thức A=x+1/(x+1) với x>1
bởi Nguyễn Bảo Yến
 30/03/2020
Ai giải hết giúp e với ạ cứu e với
30/03/2020
Ai giải hết giúp e với ạ cứu e với Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm giá trị của m để biểu thức f(x)=(-x2+4(m+1)x+1-4m^2)/(-4x^2+5x-2) luôn dương.
bởi Sunny
 26/03/2020
.
26/03/2020
.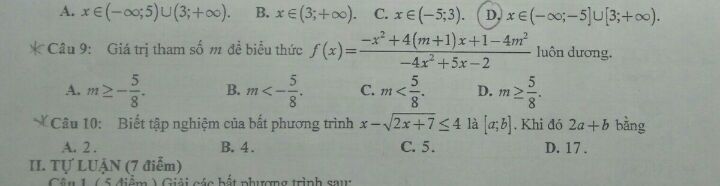 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Với giá trị nào của m thì phương trình 2x^2+2(m-1)x+3-m=0 có hai nghiệm phân biệt cùng dương.
bởi Thu Hương
 25/03/2020
Với gtri nào của m
25/03/2020
Với gtri nào của m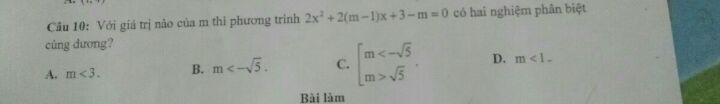 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Giải giúp em với ạ
Giải giúp em với ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải bất phương trình |x^2-3x+2|>2x-x^2
bởi Thủy Triều
 18/03/2020
18/03/2020
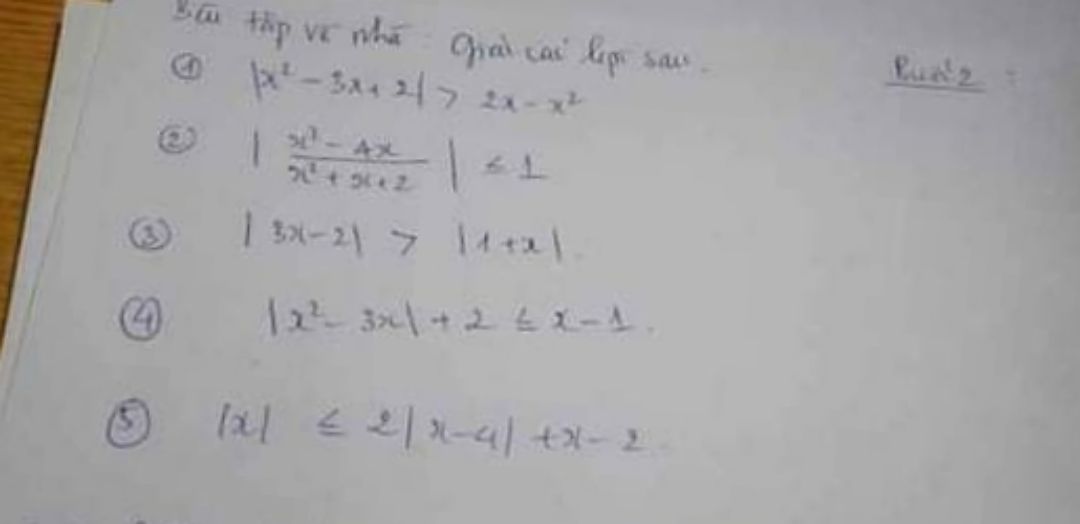 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Câu ba đó ạ
 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời -


Trắc nghiệm bất phương trình
bởi Phạm Thủy
 16/03/2020
16/03/2020
 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Tìm điều kiện m để hàm số y=(2x^3 +3)/căn((-2m+3)x^2+2mx+1) xác định với mọi x thuộc R
bởi Hạ Băng
 13/03/2020
Bài 3 ạ
13/03/2020
Bài 3 ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Định m để f(x)=mx^2-mx-5<0 với mọi x
bởi Bảo Ngân
 04/03/2020
Cần người giải cứu em nhanh ạTheo dõi (0) 0 Trả lời
04/03/2020
Cần người giải cứu em nhanh ạTheo dõi (0) 0 Trả lời -


Xác định m để phương trình (x-1)(x^2+2(m+3)x+4m+12=0 có ba nghiệm lớn hơn -1
bởi Aanh Thư
 04/03/2020
04/03/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Cho phương trình mx²-2(m 1)x m 5=0. Với giá trị nào của m thì phương trình có 2 nghiệm x1, x2 thỏa x1<0
bởi Aanh Thư
 04/03/2020
Cho phương trình mx²-2(m 1)x m 5=0. Với giá trị nào của m thì phương trình có 2 nghiệm x1, x2 thỏa x1<0Theo dõi (0) 0 Trả lời
04/03/2020
Cho phương trình mx²-2(m 1)x m 5=0. Với giá trị nào của m thì phương trình có 2 nghiệm x1, x2 thỏa x1<0Theo dõi (0) 0 Trả lời

Giải bất phương trình -3x.(x+2).(5-x) > = 0
bởi Võ Ngọc Trâm
 28/02/2020
28/02/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời

Với điều kiện nào của m để phương trình x^2-(m-1)x+m+2=0 có 2 nghiệm phân biệt?
bởi Nii Tat
 27/02/2020
27/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
 (a^3 b^3 c^3)(1/a 1/b 1/c)>=(a b c)^2
(a^3 b^3 c^3)(1/a 1/b 1/c)>=(a b c)^2 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
 Các nghiệm tự nhiên bé hơn 6 của bất phương trình 5x-1/3>12-2x/3Theo dõi (0) 1 Trả lời
Các nghiệm tự nhiên bé hơn 6 của bất phương trình 5x-1/3>12-2x/3Theo dõi (0) 1 Trả lời
 Giúp mik bài 4
Giúp mik bài 4 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời

Tìm tất cả các giá trị của m để hàm số y=căn(x^2-4x-8+m) xác định trên [0;1]
bởi Nguyen Thi Lan
 21/02/2020
giúp em với ạ
21/02/2020
giúp em với ạ Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời

 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời

Giải bất phương trình căn(x^2-4x)/(3-x) < = 2
bởi Nguyễn Huy
 20/02/2020
20/02/2020
giải hộ mk với ak .thanks
Theo dõi (0) 0 Trả lời

Giups em với ạ
Theo dõi (0) 0 Trả lời

Giải bất phương trình (2x+3).(-5x^2+8x-3)
bởi Trần Thị Thu Trâm
 16/02/2020
16/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời

Cho Bpt (m+1)x - m+2 >0. Tìm m để:
a. nghiệm đúng với mọi x
b. nghiệm đúng với mọi x>=2
c. nghiệm đúng với mọi x<1
d nghiệm đúng với mọi x thuộc[1:3]
Theo dõi (0) 1 Trả lời

Cho f(x)= 1/(1-x) + 5/x với 0<x<1
Tìm giá trị nhỏ nhất của f(x)
Theo dõi (0) 2 Trả lờiBài tập SGK khác
Bài tập 8 trang 107 SGK Đại số 10
Bài tập 9 trang 107 SGK Đại số 10
Bài tập 11 trang 107 SGK Đại số 10
Bài tập 12 trang 107 SGK Đại số 10
Bài tập 13 trang 107 SGK Đại số 10
Bài tập 14 trang 107 SGK Đại số 10
Bài tập 15 trang 108 SGK Đại số 10
Bài tập 16 trang 108 SGK Đại số 10
Bài tập 17 trang 108 SGK Đại số 10
Bài tập 4.76 trang 125 SBT Toán 10
Bài tập 4.77 trang 125 SBT Toán 10
Bài tập 4.78 trang 125 SBT Toán 10
Bài tập 4.79 trang 125 SBT Toán 10
Bài tập 4.80 trang 125 SBT Toán 10
Bài tập 4.81 trang 125 SBT Toán 10
Bài tập 4.82 trang 125 SBT Toán 10
Bài tập 4.83 trang 126 SBT Toán 10
Bài tập 4.84 trang 126 SBT Toán 10
Bài tập 76 trang 155 SGK Toán 10 NC
Bài tập 77 trang 155 SGK Toán 10 NC
Bài tập 78 trang 155 SGK Toán 10 NC
Bài tập 79 trang 155 SGK Toán 10 NC
Bài tập 80 trang 155 SGK Toán 10 NC
Bài tập 81 trang 155 SGK Toán 10 NC
Bài tập 82 trang 155 SGK Toán 10 NC
Bài tập 83 trang 156 SGK Toán 10 NC
Bài tập 84 trang 156 SGK Toán 10 NC
Bài tập 85 trang 156 SGK Toán 10 NC
Bài tập 86 trang 156 SGK Toán 10 NC
Bài tập 87 trang 156 SGK Toán 10 NC

XEM NHANH CHƯƠNG TRÌNH LỚP 10






