Giải bài 7 tr 77 sách GK sách GK Toán ĐS & GT lớp 11
Gieo một con súc sắc ba lần. Tính xác suất sao cho mặt sáu chấm xuất hiện ít nhất một lần.
Hướng dẫn giải chi tiết bài 7
Không gian mẫu gồm 216 phần tử có dạng:
\(\Omega =\left \{ (i,j,k) \setminus i,j,k \in \mathbb{Z},1\leq i,j,k\leq 6 \right \}\)
Đặt
\(A=\left \{ (6,i,j) \setminus 1\leq i,j,\leq 6 \right \}\)
\(B=\left \{ (i,6,j) \setminus 1\leq i,j,\leq 6 \right \}\)
\(C=\left \{ (i,j,6) \setminus 1\leq i,j,\leq 6 \right \}\)
Gọi biến cố có ít nhất một mặt 6 chấm xuất hiện là D.
Ta có \(D=A\cup B\cup C, n(A)=36, n(B)=36,n(C)=36\)
Mặt khác \(A\cap B=\left \{ (6,6,1);(6,6,2);(6,6,3);(6,6,4);(6,6,5);(6,6,6) \right \}\)
\(B\cap C=\left \{ (1, 6,6);(2,6,6);(3,6,6);(4,6,6);(5,6,6);(6,6,6) \right \}\)
\(C\cap A=\left \{ (6,1,6);(6,2,6);(6,3,6);(6,4,6);(6,5,6);(6,6,6) \right \}\)
\(A\cap B\cap C=\left \{ (6,6,6) \right \}\)
Dùng sơ đồ Ven ta có sự biểu diễn sau:
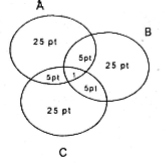
Từ sơ đồ này ta có: \(n(D)=n(A\cup B\cup C)=91\) (phần tử)
Do đó xác suất của biến cố có ít nhất mặt 6 chấm xuất hiện là: \(P(D)=\frac{91}{216}\)
-- Mod Toán 11 HỌC247
-


Số cách chọn một ban chấp hành gồm một trưởng ban, một phó ban, một thư kí, và một thủ quỹ được chọn từ 16 thành viên là:
bởi Lê Nhật Minh
 24/02/2021
24/02/2021
A. 4
B. \(\dfrac{{16!}}{4}\)
C. \(\dfrac{{16!}}{{12!.4!}}\)
D. \(\dfrac{{16!}}{{12!}}\)
Theo dõi (0) 1 Trả lời -


Trong khai triển \({\left( {8{a^2} - \dfrac{1}{2}b} \right)^6}\) hệ số của số hạng chứa \({a^6}{b^3}\) là:
bởi Spider man
 23/02/2021
23/02/2021
A. \( - 80{a^9}{b^3}\)
B. \( - 64{a^9}{b^3}\)
C. \( - 1280{a^9}{b^3}\)
D. \(60{a^6}{b^4}\)
Theo dõi (0) 1 Trả lời -


Một thầy giáo có \(5\) cuốn sách toán, \(6\) cuốn sách văn, \(7\) cuốn sách Anh văn và các cuốn sách đôi một khác nhau. Thầy giáo muốn tặng 6 cuốn sách cho 6 học sinh. Hỏi thầy giáo có bao nhiêu cách tặng nếu thầy giáo muốn sau khi tặng xong mỗi thể loại còn lại ít nhất 1 cuốn:
bởi Minh Thắng
 23/02/2021
23/02/2021
A. 13363800
B. 2585373
C. 57435543
D. 4556463
Theo dõi (0) 1 Trả lời -


Cho các số \(1, 2, 3, 4, 5, 6, 7\). Số các số tự nhiên gồm \(5\) chữ số lấy từ \(7\) chữ số trên sao cho chữ số đầu tiên bằng 3 là:
bởi Nguyễn Trà Long
 23/02/2021
23/02/2021
A. \({7^5}\)
B. \(7!\)
C. 240
D. 2401
Theo dõi (0) 1 Trả lời -


Một hội nghị bàn tròn có các phái đoàn gồm \(3\) người Anh, \(5\) người Pháp, \(7\) người Mỹ. Hỏi có bao nhiêu cách xếp chỗ ngồi cho các thành viên, sao cho những người có cùng quốc tịch thì ngồi gần nhau:
bởi Nguyễn Minh Hải
 23/02/2021
23/02/2021
A. 7257600
B. 7293732
C. 3174012
D. 1418746
Theo dõi (0) 1 Trả lời -


Một lớp có \(33\) học sinh, trong đó có \(7\) nữ. Cần chia lớp thành 3 tổ, tổ 1 có 10 học sinh, tổ 2 có 11 học sinh, tổ 3 có 12 học sinh sao cho trong mỗi tổ có ít nhất 2 học sinh nữ. Hỏi có bao nhiêu cách chia như vậy:
bởi Tường Vi
 23/02/2021
23/02/2021
A. \(C_7^3C_{26}^7\)
B. \(C_4^2C_{19}^9\)
C. \(C_7^2C_{26}^8C_5^3C_{18}^8\)
D. \(C_7^3C_{26}^7C_4^2C_{19}^9 + C_7^2C_{26}^8C_5^3C_{18}^8 + C_7^2C_{26}^8C_5^2C_{18}^9\)
Theo dõi (0) 1 Trả lời -


Từ các chữ số \(1, 2, 4, 6, 8, 9\). Lấy ngẫu nhiên một số. Xác suất để lấy được một số nguyên tố là:
bởi Co Nan
 23/02/2021
23/02/2021
A. \(\dfrac{1}{2}\)
B. \(\dfrac{1}{3}\)
C. \(\dfrac{1}{4}\)
D. \(\dfrac{1}{6}\)
Theo dõi (0) 1 Trả lời -


Có \(7\) bông hồng đỏ, \(8\) bông hồng vàng, \(10\) bông hồng trắng, mỗi bông hồng khác nhau từng đôi một. Hỏi có bao nhiêu cách lấy 3 bông hồng có đủ 3 màu:
bởi Meo Thi
 23/02/2021
23/02/2021
A. 3014
B. 310
C. 560
D. 319
Theo dõi (0) 1 Trả lời -


Số hạng không chứa \(x\) trong khai triển \({\left( {{x^3} + \dfrac{1}{{{x^3}}}} \right)^{18}}\) là:
bởi Hữu Nghĩa
 23/02/2021
23/02/2021
A. \(C_{18}^9\)
B. \(C_{18}^{10}\)
C. \(C_{18}^8\)
D. \(C_{18}^3\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5 trang 76 SGK SGK Đại số & Giải tích 11
Bài tập 6 trang 76 SGK SGK Đại số & Giải tích 11
Bài tập 8 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 9 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 10 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 11 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 12 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 13 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 14 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 15 trang 77 SGK SGK Đại số & Giải tích 11
Bài tập 2.57 trang 86 SBT Toán 11
Bài tập 2.58 trang 86 SBT Toán 11
Bài tập 2.59 trang 86 SBT Toán 11
Bài tập 2.60 trang 86 SBT Toán 11
Bài tập 2.61 trang 87 SBT Toán 11
Bài tập 2.62 trang 87 SBT Toán 11
Bài tập 2.63 trang 87 SBT Toán 11
Bài tập 2.64 trang 87 SBT Toán 11
Bài tập 2.65 trang 87 SBT Toán 11
Bài tập 2.66 trang 87 SBT Toán 11
Bài tập 43 trang 90 SGK Toán 11 NC
Bài tập 44 trang 90 SGK Toán 11 NC
Bài tập 45 trang 90 SGK Toán 11 NC
Bài tập 46 trang 90 SGK Toán 11 NC
Bài tập 47 trang 91 SGK Toán 11 NC
Bài tập 48 trang 91 SGK Toán 11 NC
Bài tập 49 trang 91 SGK Toán 11 NC
Bài tập 50 trang 92 SGK Toán 11 NC
Bài tập 51 trang 92 SGK Toán 11 NC
Bài tập 52 trang 92 SGK Toán 11 NC
Bài tập 53 trang 93 SGK Toán 11 NC
Bài tập 54 trang 93 SGK Toán 11 NC
Bài tập 55 trang 93 SGK Toán 11 NC
Bài tập 56 trang 93 SGK Toán 11 NC
Bài tập 57 trang 93 SGK Toán 11 NC
Bài tập 58 trang 93 SGK Toán 11 NC
Bài tập 59 trang 94 SGK Toán 11 NC
Bài tập 60 trang 94 SGK Toán 11 NC
Bài tập 61 trang 94 SGK Toán 11 NC
Bài tập 62 trang 94 SGK Toán 11 NC
Bài tập 63 trang 94 SGK Toán 11 NC
Bài tập 64 trang 94 SGK Toán 11 NC
Bài tập 65 trang 94 SGK Toán 11 NC
Bài tập 66 trang 94 SGK Toán 11 NC
Bài tập 67 trang 94 SGK Toán 11 NC
Bài tập 68 trang 95 SGK Toán 11 NC
Bài tập 69 trang 95 SGK Toán 11 NC
Bài tập 70 trang 95 SGK Toán 11 NC
Bài tập 71 trang 95 SGK Toán 11 NC





