Bài tập 55 tr 63 sách GK Toán lớp 9 Tập 2
Cho phương trình: x2 - x - 2 = 0.
a) Giải phương trình.
b) Vẽ hai đồ thị y = x2 và y = x + 2 trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Giải phương trình bằng cách sử dụng công thức nghiệm hoặc
+) Xét phương trình bậc hai: \(a{x^2} + bx + c = 0\,(a \ne 0).\)
Nếu phương trình có \(a - b + c = 0\) thì phương trình có một nghiệm là \({x_1} = - 1,\) nghiệm kia là \({x_2} = - \dfrac{c}{a}.\)
b) Lập bảng giá trị rồi vẽ hai đồ thị hàm số \(y = {x^2};y = x + 2\)
c) Thay hai nghiệm tìm được ở câu a) vào mỗi hàm số để so sánh các giá trị của \(y.\)
Lời giải chi tiết
a)
Giải phương trình: \(x^2 – x – 2 = 0\)
\(\Delta = (-1)^2– 4.1.(-2) = 1 + 8 > 0\)
\(\sqrt\Delta= \sqrt9 = 3\)
\(\Rightarrow {x_1} = -1; {x_2}= 2\)
b)
Vẽ đồ thị hàm số
- Hàm số \(y = x^2\)
+ Bảng giá trị:
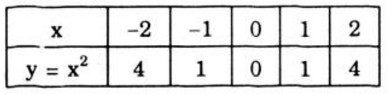
- Hàm số \(y = x + 2\)
+ Cho \(x = 0 ⇒ y = 2\) được điểm \(A(0;2)\)
+ Cho \(x = -2 ⇒ y = 0\) được điểm \(B(-2;0)\)
Đồ thị hàm số:
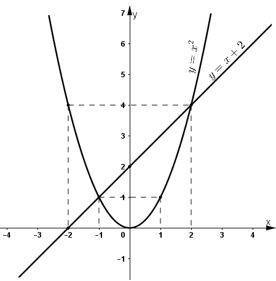
c)
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\({x^2} = x + 2 \Leftrightarrow {x^2} - x - 2 = 0\) có \(a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\) nên có hai nghiệm \({x_1} = - 1;{x_2} = 2.\)
Điều này chứng tỏ rằng đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là \(x = -1; x= 2\). Hai giá trị này cũng chính là nghiệm của phương trình \(x^2 - x - 2 = 0\) ở câu a).
-- Mod Toán 9 HỌC247
-


Cho phương trình sau \({x^2} + 4x + m + 1 = 0\,\,\,(1)\) (với m là tham số). Hãy tìm điều kiện của m để phương trình (1) có nghiệm.
bởi A La
 11/07/2021
11/07/2021
Cho phương trình sau \({x^2} + 4x + m + 1 = 0\,\,\,(1)\) (với m là tham số). Hãy tìm điều kiện của m để phương trình (1) có nghiệm.
Theo dõi (0) 1 Trả lời -


Cho phương trình sau \({x^2} + 4x + m + 1 = 0\,\,\,(1)\) (với m là tham số). Hãy giải phương trình (1) với m = 2.
bởi Ngọc Trinh
 11/07/2021
11/07/2021
Cho phương trình sau \({x^2} + 4x + m + 1 = 0\,\,\,(1)\) (với m là tham số). Hãy giải phương trình (1) với m = 2.
Theo dõi (0) 1 Trả lời -


Giải hệ sau \(\left\{ \begin{array}{l}x - y = 4\\2x - y = 5\end{array} \right..\)
bởi Hữu Nghĩa
 11/07/2021
11/07/2021
Giải hệ sau \(\left\{ \begin{array}{l}x - y = 4\\2x - y = 5\end{array} \right..\)
Theo dõi (0) 1 Trả lời -


Hãy rút gọn biểu thức sau: \(B = \dfrac{{a + 2\sqrt a }}{{\sqrt a + 2}} - \dfrac{{a - 4}}{{\sqrt a - 2}}\) (với \(a \ge 0,\;\;a \ne 4\)).
bởi Naru to
 12/07/2021
12/07/2021
Hãy rút gọn biểu thức sau: \(B = \dfrac{{a + 2\sqrt a }}{{\sqrt a + 2}} - \dfrac{{a - 4}}{{\sqrt a - 2}}\) (với \(a \ge 0,\;\;a \ne 4\)).
Theo dõi (0) 1 Trả lời -


Hãy rút gọn biểu thức sau: \(A = \sqrt {45} + \sqrt {20} - 2\sqrt 5 .\)
Theo dõi (0) 1 Trả lời -


Cho giá trị a, b là hai số thực dương thỏa mãn \(a + b \le 4\). Tìm giá trị nhỏ nhất của biểu thức \(S = \dfrac{1}{{{a^2} + {b^2}}} + \dfrac{{25}}{{ab}} + ab\)
bởi Phung Thuy
 11/07/2021
11/07/2021
Cho giá trị a, b là hai số thực dương thỏa mãn \(a + b \le 4\). Tìm giá trị nhỏ nhất của biểu thức \(S = \dfrac{1}{{{a^2} + {b^2}}} + \dfrac{{25}}{{ab}} + ab\)
Theo dõi (0) 1 Trả lời -


Cho hai số dương là \(x,\,y\), có \(x + y = 1\). Tìm giá trị nhỏ nhất của biểu thức \(B = \left( {1 - \dfrac{1}{{{x^2}}}} \right)\left( {1 - \dfrac{1}{{{y^2}}}} \right).\)
bởi Lê Bảo An
 10/07/2021
10/07/2021
Cho hai số dương là \(x,\,y\), có \(x + y = 1\). Tìm giá trị nhỏ nhất của biểu thức \(B = \left( {1 - \dfrac{1}{{{x^2}}}} \right)\left( {1 - \dfrac{1}{{{y^2}}}} \right).\)
Theo dõi (0) 1 Trả lời -


Có parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,\,y = mx + 2\). Với \(m = - 1\). Tìm các giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) sao cho \({x_1} - 2{x_2} = 5.\)
bởi Đào Lê Hương Quỳnh
 10/07/2021
10/07/2021
Có parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,\,y = mx + 2\). Với \(m = - 1\). Tìm các giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) sao cho \({x_1} - 2{x_2} = 5.\)
Theo dõi (0) 1 Trả lời -


Có parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,\,y = mx + 2\). Với \(m = - 1\). Tìm tọa độ các giao điểm của \(\left( P \right)\) và \(\left( d \right).\)
bởi Nguyễn Ngọc Sơn
 10/07/2021
10/07/2021
Có parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,\,y = mx + 2\). Với \(m = - 1\). Tìm tọa độ các giao điểm của \(\left( P \right)\) và \(\left( d \right).\)
Theo dõi (0) 1 Trả lời -


Giải hệ sau: \(\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} + \dfrac{4}{{3y + 1}} = 5\\\dfrac{2}{{x - 2}} - \dfrac{4}{{3y + 1}} = - 2\end{array} \right.\)
bởi Dang Thi
 10/07/2021
10/07/2021
Giải hệ sau: \(\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} + \dfrac{4}{{3y + 1}} = 5\\\dfrac{2}{{x - 2}} - \dfrac{4}{{3y + 1}} = - 2\end{array} \right.\)
Theo dõi (0) 1 Trả lời -


Ở một cửa hàng phục vụ hai loại bánh pizza có dạng hình trụ, độ dày giống nhau nhưng khác nhau về kích thước. Loại nhỏ có đường kính 30 cm giá 60000 đồng, loại lớn có đường kính 40 cm giá 80000 đồng. Vậy mua cái nào lợi hơn? Vì sao?
bởi Hy Vũ
 10/07/2021
10/07/2021
Ở một cửa hàng phục vụ hai loại bánh pizza có dạng hình trụ, độ dày giống nhau nhưng khác nhau về kích thước. Loại nhỏ có đường kính 30 cm giá 60000 đồng, loại lớn có đường kính 40 cm giá 80000 đồng. Vậy mua cái nào lợi hơn? Vì sao?
Theo dõi (0) 1 Trả lời -


Có một xe ô tô con và một xe ô tô tải khởi hành cùng một lúc đi từ A đến B. Vận tốc của xe ô tô con lớn hơn vận tốc của xe ô tô tải là 10 km/h nên xe ô tô con đến B sớm hơn xe ô tô tải là 30 phút. Tính vận tốc của mỗi xe biết quãng đường AB dài 100 km.
bởi Trung Phung
 10/07/2021
10/07/2021
Có một xe ô tô con và một xe ô tô tải khởi hành cùng một lúc đi từ A đến B. Vận tốc của xe ô tô con lớn hơn vận tốc của xe ô tô tải là 10 km/h nên xe ô tô con đến B sớm hơn xe ô tô tải là 30 phút. Tính vận tốc của mỗi xe biết quãng đường AB dài 100 km.
Theo dõi (0) 1 Trả lời -


Với (B = \dfrac{{\sqrt x }}{{\sqrt x - 1}} - \dfrac{5}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 4}}{{x - 1}}\) với \(x > 0,\,\,x \ne 1\). Chứng minh \(B = \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}}.\)
bởi Nguyễn Quang Thanh Tú
 10/07/2021
10/07/2021
Với (B = \dfrac{{\sqrt x }}{{\sqrt x - 1}} - \dfrac{5}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 4}}{{x - 1}}\) với \(x > 0,\,\,x \ne 1\). Chứng minh \(B = \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}}.\)
Theo dõi (0) 1 Trả lời -


Với biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x + 1}}\). Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
bởi Tran Chau
 10/07/2021
10/07/2021
Với biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x + 1}}\). Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
Theo dõi (0) 1 Trả lời -


Cho các số thực là \(x,y\) thỏa mãn \({x^2} + {y^2} - 4x + 3 = 0\). Tìm giá trị lớn nhất và nhỏ nhất của biểu thức \(A = {x^2} + {y^2}.\)
bởi Nguyễn Thủy
 09/07/2021
09/07/2021
Cho các số thực là \(x,y\) thỏa mãn \({x^2} + {y^2} - 4x + 3 = 0\). Tìm giá trị lớn nhất và nhỏ nhất của biểu thức \(A = {x^2} + {y^2}.\)
Theo dõi (0) 1 Trả lời -


Cho \({x^2} - 2x + m - 3 = 0\) (\(m\) là tham số). Hãy tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn điều kiện \({x_1} = 3{x_2}.\)
bởi Anh Tuyet
 10/07/2021
10/07/2021
Cho \({x^2} - 2x + m - 3 = 0\) (\(m\) là tham số). Hãy tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn điều kiện \({x_1} = 3{x_2}.\)
Theo dõi (0) 1 Trả lời -


Cho \({x^2} - 2x + m - 3 = 0\) (\(m\) là tham số). Giải phương trình khi \(m = - 5\)
bởi Bánh Mì
 10/07/2021
10/07/2021
Cho \({x^2} - 2x + m - 3 = 0\) (\(m\) là tham số). Giải phương trình khi \(m = - 5\)
Theo dõi (0) 1 Trả lời -


Hãy giải hệ sau: \(\left\{ \begin{array}{l}x + \sqrt {2y - 5} = 12\\2x - \sqrt {2y - 5} = 3\end{array} \right.\)
bởi Đào Lê Hương Quỳnh
 10/07/2021
10/07/2021
Hãy giải hệ sau: \(\left\{ \begin{array}{l}x + \sqrt {2y - 5} = 12\\2x - \sqrt {2y - 5} = 3\end{array} \right.\)
Theo dõi (0) 1 Trả lời -


Có một đoàn xe vận tải dự định sử dụng một số xe cùng loại để chuyên chở 90 tấn thiết bị y tế. Để đáp ứng kịp nhu cầu phục vụ công tác phòng chống dịch Covid – 19 đoàn được bổ sung thêm 5 chiếc xe cùng loại. Do đó mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn. Biết khối lượng hàng mỗi xe chuyên chở như nhau, hỏi ban đầu đoàn xe có bao nhiêu chiếc?
bởi thùy trang
 10/07/2021
10/07/2021
Có một đoàn xe vận tải dự định sử dụng một số xe cùng loại để chuyên chở 90 tấn thiết bị y tế. Để đáp ứng kịp nhu cầu phục vụ công tác phòng chống dịch Covid – 19 đoàn được bổ sung thêm 5 chiếc xe cùng loại. Do đó mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn. Biết khối lượng hàng mỗi xe chuyên chở như nhau, hỏi ban đầu đoàn xe có bao nhiêu chiếc?
Theo dõi (0) 1 Trả lời -


Cho hai biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x + 1}} - \dfrac{6}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\) và \(B = \dfrac{2}{{\sqrt x - 2}}\) với \(x \ge 0\) và \(x \ne 4.\) Biết \(P = A + B.\) Chứng minh \(P = \dfrac{{\sqrt x + 2}}{{\sqrt x + 1}}\)
bởi Anh Linh
 10/07/2021
10/07/2021
Cho hai biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x + 1}} - \dfrac{6}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\) và \(B = \dfrac{2}{{\sqrt x - 2}}\) với \(x \ge 0\) và \(x \ne 4.\) Biết \(P = A + B.\) Chứng minh \(P = \dfrac{{\sqrt x + 2}}{{\sqrt x + 1}}\)
Theo dõi (0) 1 Trả lời -


Có biểu thức B sau: \(B = \dfrac{2}{{\sqrt x - 2}}\) với \(x \ge 0\) và \(x \ne 4.\) Tính giá trị biểu thức \(B\) khi \(x = 16.\)
bởi bach hao
 10/07/2021
10/07/2021
Có biểu thức B sau: \(B = \dfrac{2}{{\sqrt x - 2}}\) với \(x \ge 0\) và \(x \ne 4.\) Tính giá trị biểu thức \(B\) khi \(x = 16.\)
Theo dõi (0) 1 Trả lời -


Cho ba số thực dương x, y, z thỏa điều kiện x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{x}{{{y^2} + 1}} + \dfrac{y}{{{z^2} + 1}} + \dfrac{z}{{{x^2} + 1}}\)
bởi Dell dell
 10/07/2021
10/07/2021
Cho ba số thực dương x, y, z thỏa điều kiện x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{x}{{{y^2} + 1}} + \dfrac{y}{{{z^2} + 1}} + \dfrac{z}{{{x^2} + 1}}\)
Theo dõi (0) 1 Trả lời -


Cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x + m - 1\). Tìm giá trị m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thỏa mãn \(x_1^3 + x_2^3 = 9\)
bởi Nguyễn Thị Lưu
 10/07/2021
10/07/2021
Cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x + m - 1\). Tìm giá trị m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thỏa mãn \(x_1^3 + x_2^3 = 9\)
Theo dõi (0) 1 Trả lời -


Cho Parabol như sau \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x + m - 1\). Tìm tọa độ giao điểm của đường thẳng (d) và parabol (P) khi m = 5.
bởi Bảo Anh
 10/07/2021
10/07/2021
Cho Parabol như sau \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x + m - 1\). Tìm tọa độ giao điểm của đường thẳng (d) và parabol (P) khi m = 5.
Theo dõi (0) 1 Trả lời -


Ở một cửa hàng bán xăng dầu dự định đặt làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều cao 1,8 m, bán kính đáy 0,6 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu? (Bỏ qua bề dầy của bồn)
bởi hà trang
 10/07/2021
10/07/2021
Ở một cửa hàng bán xăng dầu dự định đặt làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều cao 1,8 m, bán kính đáy 0,6 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu? (Bỏ qua bề dầy của bồn)
Theo dõi (0) 1 Trả lời -


Theo kế hoạch, trong tháng 3 năm 2020 hai tổ phải may 1500 chiếc khẩu trang để phục vụ cho công tác phòng, chống dịch Covid-19. Nhưng thực tế tổ I đã may vượt mức 10%; tổ II may vượt mức 12% nên cả hai tổ đã may được 1664 chiếc khẩu trang. Cho biết theo kế hoạch mỗi tổ phải may bao nhiêu chiếc khẩu trang?
bởi Phung Thuy
 10/07/2021
10/07/2021
Theo kế hoạch, trong tháng 3 năm 2020 hai tổ phải may 1500 chiếc khẩu trang để phục vụ cho công tác phòng, chống dịch Covid-19. Nhưng thực tế tổ I đã may vượt mức 10%; tổ II may vượt mức 12% nên cả hai tổ đã may được 1664 chiếc khẩu trang. Cho biết theo kế hoạch mỗi tổ phải may bao nhiêu chiếc khẩu trang?
Theo dõi (0) 1 Trả lời -


Ở một trường tổ chức cho 250 người bao gồm giáo viên và học sinh đi tham quan Suối Tiên. Biết giá vé vào cổng giáo viên là 80.000 đồng, học sinh là 60.000 đồng, đi vào đúng dịp giỗ tổ Hùng Vương nên giảm 5% vé vào, vì vậy nhà trường phải trả tổng cộng 14.535.000 đồng. Hỏi có bao nhiêu giáo viên và học sinh đi tham quan?
bởi Anh Trần
 10/07/2021
10/07/2021
Ở một trường tổ chức cho 250 người bao gồm giáo viên và học sinh đi tham quan Suối Tiên. Biết giá vé vào cổng giáo viên là 80.000 đồng, học sinh là 60.000 đồng, đi vào đúng dịp giỗ tổ Hùng Vương nên giảm 5% vé vào, vì vậy nhà trường phải trả tổng cộng 14.535.000 đồng. Hỏi có bao nhiêu giáo viên và học sinh đi tham quan?
Theo dõi (0) 1 Trả lời -


Cho phương trình sau: \({x^2} - 2mx - 4m - 5 = 0.\) Tìm giá trị m để phương trình có 2 nghiệm phân biệt thỏa mãn: \(x_1^2 + x_2^2 - {x_1}{x_2} = 2{x_1} + 2{x_2} + 27.\)
bởi Nguyen Ngoc
 10/07/2021
10/07/2021
Cho phương trình sau: \({x^2} - 2mx - 4m - 5 = 0.\) Tìm giá trị m để phương trình có 2 nghiệm phân biệt thỏa mãn: \(x_1^2 + x_2^2 - {x_1}{x_2} = 2{x_1} + 2{x_2} + 27.\)
Theo dõi (0) 1 Trả lời -


Cho phương trình: \({x^2} - 2mx - 4m - 5 = 0.\) Chứng tỏ rằng phương trình trên luôn có 2 nghiệm phân biệt với mọi m.
bởi Trịnh Lan Trinh
 10/07/2021
10/07/2021
Cho phương trình: \({x^2} - 2mx - 4m - 5 = 0.\) Chứng tỏ rằng phương trình trên luôn có 2 nghiệm phân biệt với mọi m.
Theo dõi (0) 1 Trả lời -


Biết một mảnh đất hình chữ nhật có chu vi 80m, biết ba lần chiều rộng kém 2 lần chiều dài là 5m. Hãy tính diện tích mảnh đất.
bởi Nguyễn Vân
 10/07/2021
10/07/2021
Biết một mảnh đất hình chữ nhật có chu vi 80m, biết ba lần chiều rộng kém 2 lần chiều dài là 5m. Hãy tính diện tích mảnh đất.
Theo dõi (0) 1 Trả lời -


Hãy giải phương trình sau đây: \({(x + 1)^2} - 2x + 1 = {x^4}.\)
Theo dõi (0) 1 Trả lời -


Hãy giải phương trình sau đây: \(3x(x - 2) = 11 - 2{x^2}.\)
Theo dõi (0) 1 Trả lời -


Điều kiện của m để phương trình \({x^2} - 2mx + {m^2} - 4 = 0\) có hai nghiệm \({x_1} = 0,\,\,{x_2} > 0\) là bằng:
bởi Bo Bo
 10/07/2021
10/07/2021
A. \(m = - 2\) B. \(m = 2\)
C. \(m = \pm 2\) D. \(m = 16\)
Theo dõi (0) 1 Trả lời -


Cho biết cặp số \(\left( { - 1;2} \right)\) là nghiệm của hệ phương trình nào sau đây?
bởi Lê Tấn Vũ
 10/07/2021
10/07/2021
A. \(\left\{ \begin{array}{l}x + 5y = 9\\6x + 2y = - 2\end{array} \right.\)
B. \(\left\{ \begin{array}{l} - 2x + y = 7\\x - \dfrac{3}{4}y = 3\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x + y = 1\\ - 2x + y = 4\end{array} \right.\)
D. \(\left\{ \begin{array}{l}2x - 2y = 0\\x + y = 3\end{array} \right.\)
Theo dõi (0) 1 Trả lời -


Giả sử \(x,y\) là các số thực dương thỏa mãn \(x + y = 2.\) Tìm giá trị lớn nhất của \(A = xy\left( {{x^3} + {y^3}} \right).\)
bởi Truc Ly
 10/07/2021
10/07/2021
Giả sử \(x,y\) là các số thực dương thỏa mãn \(x + y = 2.\) Tìm giá trị lớn nhất của \(A = xy\left( {{x^3} + {y^3}} \right).\)
Theo dõi (0) 1 Trả lời -


Ở Sở Giáo dục và Đào tạo Bắc Ninh dự định tổ chức hội nghị tại hội trường \(500\) chỗ ngồi của trường THPT chuyên Bắc Ninh, hội trường được chia thành từng dãy ghế, mỗi dãy ghế có số chỗ ngồi như nhau. Vì có \(567\) người dự hội nghị nên ban tổ chức phải kê thêm \(1\) dãy ghế, đồng thời phải kê thêm \(2\) chỗ ngồi cho tất cả các dãy ghế thì vừa đủ số chỗ ngồi. Hỏi lúc đầu hội trường có bao nhiêu dãy ghế và mỗi dãy ghế có bao nhiêu chỗ ngồi?
bởi Nguyễn Trọng Nhân
 10/07/2021
10/07/2021
Ở Sở Giáo dục và Đào tạo Bắc Ninh dự định tổ chức hội nghị tại hội trường \(500\) chỗ ngồi của trường THPT chuyên Bắc Ninh, hội trường được chia thành từng dãy ghế, mỗi dãy ghế có số chỗ ngồi như nhau. Vì có \(567\) người dự hội nghị nên ban tổ chức phải kê thêm \(1\) dãy ghế, đồng thời phải kê thêm \(2\) chỗ ngồi cho tất cả các dãy ghế thì vừa đủ số chỗ ngồi. Hỏi lúc đầu hội trường có bao nhiêu dãy ghế và mỗi dãy ghế có bao nhiêu chỗ ngồi?
Theo dõi (0) 1 Trả lời -


Cho \({x^2} - 2mx + {m^2} - m + 1 = 0,\) với \(x\) là ẩn; \(m\) là tham số. Hãy tìm \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1}^2 + {x_2}^2 = {x_1}{x_2} + 1\)
bởi Ban Mai
 10/07/2021
10/07/2021
Cho \({x^2} - 2mx + {m^2} - m + 1 = 0,\) với \(x\) là ẩn; \(m\) là tham số. Hãy tìm \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1}^2 + {x_2}^2 = {x_1}{x_2} + 1\)
Theo dõi (0) 1 Trả lời -


Cho phương trình sau \({x^2} - 2mx + {m^2} - m + 1 = 0,\) với \(x\) là ẩn; \(m\) là tham số. Hãy giải phương trình với \(m = 2.\)
bởi Pham Thi
 10/07/2021
10/07/2021
Cho phương trình sau \({x^2} - 2mx + {m^2} - m + 1 = 0,\) với \(x\) là ẩn; \(m\) là tham số. Hãy giải phương trình với \(m = 2.\)
Theo dõi (0) 1 Trả lời -


Cho \(A = \dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x - 3}} + \dfrac{{3x + 9}}{{9 - x}},\) với \(x \ge 0\,;\,\,x \ne 9.\) Rút gọn biểu thức \(A\) đã cho
bởi Bảo khanh
 09/07/2021
09/07/2021
Cho \(A = \dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x - 3}} + \dfrac{{3x + 9}}{{9 - x}},\) với \(x \ge 0\,;\,\,x \ne 9.\) Rút gọn biểu thức \(A\) đã cho
Theo dõi (0) 1 Trả lời -


Số giá trị nguyên của \(m\) để hàm số \(y = \left( {{m^2} - 9} \right)x + 3\) nghịch biến là bằng:
bởi Nguyễn Thanh Thảo
 10/07/2021
10/07/2021
A. \(5\) B. \(4\)
C. \(2\) D. \(3\)
Theo dõi (0) 1 Trả lời -


Giá trị của biểu thức sau \(P = \sqrt {3 + 2\sqrt 2 } - \sqrt {3 - 2\sqrt 2 } \) là bằng?
bởi Nguyễn Thị Thúy
 10/07/2021
10/07/2021
A. \(2\sqrt 2 \)
B. \( - 2\)
C. \(2\)
D. \( - 2\sqrt 2 \)
Theo dõi (0) 1 Trả lời -


Điều kiện để biểu thức \(M = \dfrac{1}{{\sqrt x - 1}}\) xác định là đáp án?
bởi Nguyễn Anh Hưng
 10/07/2021
10/07/2021
A. \(x > 1\)
B. \(x > 0\)
C. \(x > 0\,\,;\,\,x \ne 1\)
D. \(x \ge 0\,\,;\,\,x \ne 1\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Câu hỏi 5 trang 61 SGK Toán 9 Tập 2
Bài tập 54 trang 63 SGK Toán 9 Tập 2
Bài tập 56 trang 63 SGK Toán 9 Tập 2
Bài tập 57 trang 63 SGK Toán 9 Tập 2
Bài tập 58 trang 63 SGK Toán 9 Tập 2
Bài tập 59 trang 63 SGK Toán 9 Tập 2
Bài tập 60 trang 64 SGK Toán 9 Tập 2
Bài tập 61 trang 64 SGK Toán 9 Tập 2
Bài tập 62 trang 64 SGK Toán 9 Tập 2
Bài tập 63 trang 64 SGK Toán 9 Tập 2
Bài tập 64 trang 64 SGK Toán 9 Tập 2
Bài tập 65 trang 64 SGK Toán 9 Tập 2
Bài tập 66 trang 64 SGK Toán 9 Tập 2
Bài tập 67 trang 63 SBT Toán 9 Tập 2
Bài tập 68 trang 63 SBT Toán 9 Tập 2
Bài tập 69 trang 63 SBT Toán 9 Tập 2
Bài tập 70 trang 63 SBT Toán 9 Tập 2
Bài tập 71 trang 63 SBT Toán 9 Tập 2
Bài tập 72 trang 63 SBT Toán 9 Tập 2
Bài tập 73 trang 63 SBT Toán 9 Tập 2
Bài tập 73 trang 63 SBT Toán 9 Tập 2
Bài tập 74 trang 63 SBT Toán 9 Tập 2
Bài tập 74 trang 63 SBT Toán 9 Tập 2
Bài tập 4.1 trang 64 SBT Toán 9 Tập 2
Bài tập 4.2 trang 64 SBT Toán 9 Tập 2
Bài tập 4.3 trang 64 SBT Toán 9 Tập 2





