Bài tập 54 trang 63 SGK Toán 9 Tập 2

33 BT SGK

Bài tập 54 tr 63 sách GK Toán lớp 9 Tập 2

Vẽ đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = - {1 \over 4}{x^2}\) trên cùng một hệ trục tọa độ

a) Qua điểm \(B(0; 4)\) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số \(\displaystyle y = - {1 \over 4}{x^2}\) điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

- Ước lượng trên hình vẽ:

- Tính toán theo công thức.

Toán 9 Chương 4 Bài 9 Trắc nghiệm Toán 9 Chương 4 Bài 9 Giải bài tập Toán 9 Chương 4 Bài 9

Hướng dẫn giải chi tiết

Hướng dẫn giải

Các bước vẽ đồ thị hàm số \(y=a{x^2}\)

- Bước 1: lập bảng giá trị x, y tương ứng (ít nhất 5 giá trị)

- Bước 2: Vẽ đồ thị hàm số: Nối các điểm trên hệ trục tọa độ, ta được đồ thị hàm số \(y=a{x^2}\)

+) Đồ thị hàm số \(y=a{x^2}\) với \(a \ne 0\) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là 1 parabol đỉnh O.

a) Giải phương trình hoành độ giao điểm \(\dfrac {1}{4}x^2=4\) để tìm hoành độ của M và M'

b) Điểm \(N(x_N;y_N)\) thuộc đồ thị hàm số \(y=f(x)\) thì \(y_N=f(x_N)\)

Lời giải chi tiết

Vẽ đồ thị hàm số:

* Hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = - {1 \over 4}{x^2}\)

- Tập xác định \(D = R\)

- Bảng giá trị

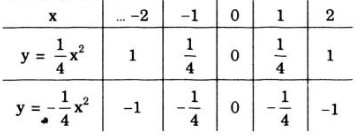
- Đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = - {1 \over 4}{x^2}\) là các Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) nằm trên trục hoành, đồ thị hàm số \(\displaystyle y = - {1 \over 4}{x^2}\) nằm dưới trục hoành.

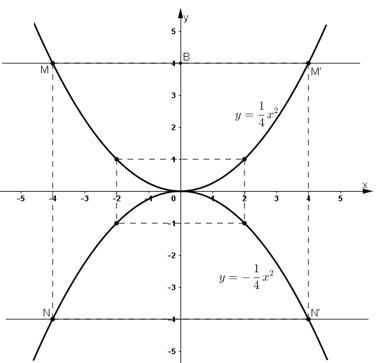
a) Đường thẳng qua \(B(0; 4)\) song song với \(Ox\) có dạng: y = 4.

Phương trình hoành độ giao điểm của đường thẳng y = 4 và đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) là:

\(\dfrac{1}{4}{x^2} = 4 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = \pm 4\)

Từ đó ta có hoành độ của \(M\) là \(x = 4\), của \(M'\) là \(x = - 4\).

b) Trên đồ thị hàm số \(\displaystyle y = - {1 \over 4}{x^2}\) ta xác định được điểm \(N\) và \(N’\) có cùng hoành độ với \(M, M’\). Ta được đường thẳng \(NN'//Ox\)

Tìm tung độ của \(N, N’\)

- Ước lượng trên hình vẽ được tung độ của \(N\) là \(y = - 4\); của \(N’\) là \(y = -4\)

- Tính toán theo công thức:

Điểm \(N(4;y)\). Thay \(x = 4\) vào \(\displaystyle y = - {1 \over 4}{x^2}\) nên \(\displaystyle y = - {1 \over 4}{.4^2} = - 4\)

Điểm \(N’(-4;y)\). Thay \(x = - 4\) vào \(\displaystyle y = - {1 \over 4}{x^2}\) nên \(\displaystyle y = - {1 \over 4}.{( - 4)^2} = - 4\)

Vậy tung độ của \(N, N’\) cùng bằng \(-4\).

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 54 trang 63 SGK Toán 9 Tập 2 HAY thì click chia sẻ

YOMEDIA