Giải bài 67 tr 63 sách BT Toán lớp 9 Tập 2
Cho hai hàm số: \(y = 2x - 3\) và \(y = - {x^2}\)
a) Vẽ đồ thị hai hàm số này trong cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị.
c) Kiểm nghiệm rằng tọa độ của mỗi giao điểm đều là nghiệm chung của hai phương trình hai ẩn y = 2x – 3 và \(y = - {x^2}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Xác định các điểm thuộc đồ thị rồi vẽ đồ thị hàm số.
b) Tìm tọa độ các giao điểm của hai đồ thị.
c) Thay tọa độ giao điểm vào mỗi phương trình để suy ra nghiệm.
Lời giải chi tiết
a) Vẽ đồ thị hàm số: \(y = 2x - 3\)
Cho x = 0 ⇒ y = -3(0; -3)
Cho y = 0 ⇒ x = 1,5(1,5; 0)
Vẽ đồ thị hàm số:
|
x |
-2 |
-1 |
0 |
1 |
2 |
| \(y = - {x^2}\) |
-4 |
-1 |
0 |
-1 |
-4 |
b) Tọa độ giao điểm của hai đồ thị: A(1; -1) và B(-3; -9)
c) Thay tọa độ của A và B vào phương trình: \(y = 2x - 3\) ta có:
\( - 1 = 2.1 - 3; - 9 = 2.\left( { - 3} \right) - 3\)
Thay tọa độ của A và B vào phương trình: \(y = - {x^2}\)
\( - 1 = - {1^2} = - 1; - 9 = - {\left( { - 3} \right)^2} = - 9\)
Vậy tọa độ của A và B là nghiệm của hệ phương trình:
\(\left\{ {\matrix{
{y = 2x - 3} \cr
{y = - {x^2}} \cr} } \right.\)
-- Mod Toán 9 HỌC247
-


Giải hệ phương trình x+y=m và 2x-my=0 khi m=-1
bởi Lâm Như
 22/03/2020
22/03/2020
Cho hpt:x+y=m
2x-my=0
a. Giải hpt trên khi m=-1
b. Xác định giá trị của m để :
1) x=1 , y=1 là nghiệm của hpt trên
2) Hệ phương trình vô nghiệm
c. Tìm nghiệm của hpt theo m
d.Tìm m để hpt có nghiệm (x,y) thỏa : x+y=1
Theo dõi (0) 3 Trả lời -


Tìm m để phương trình x2 - (2m-1) + m2-1=0 có hai nghiệm x1, x2 thoả mãn: (x1-x2)2=x1-3x2
bởi Thùy Duyên
 21/03/2020
21/03/2020
Cho phương trình: x2 - (2m-1) + m2-1=0 Xác định m để hai nghiệm x1, x2 của pt thoả mãn: (x1-x2)2=x1-3x2
Theo dõi (1) 0 Trả lời -


Cho hàm y=(m-2)x+n tìm giá trị của m và n để đồ thị hàm sô đi qua điểm A(-1,2) và điểm B(3,4).
bởi Nguyễn Nghị
 20/03/2020
20/03/2020
cho hàm y=(m-2)x+n tìm giá trị của m và n để đồ thị hàm sô đi qua điểm A(-1,2) và điểm B(3,4)
Theo dõi (0) 1 Trả lời -


giải phương trình
(12x - 1)(6x - 1)(4x - 1)(3x - 1)=5
Theo dõi (0) 1 Trả lời -


Giải phương trình 6x^2+7x-20=0
bởi Nguyễn Lý Thùy Trâm
 19/03/2020
Làm giúp mình bài 4 và 5 nhé. Cảm ơn mọi người nhiều lắm.
19/03/2020
Làm giúp mình bài 4 và 5 nhé. Cảm ơn mọi người nhiều lắm. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính √(4+2√3) +√(4-2√3)
bởi Lê Ngân
 17/03/2020
17/03/2020
giải phép tính sau:
căng (4 + 2 căng 3) + căng ( 4 - 2 căng 3 )
Theo dõi (0) 2 Trả lời -


Tìm x sao cho x(x + 1)(x + 2)(x + 3)=24
bởi Nguyễn Việt Tiến
 16/03/2020
16/03/2020
tìm x sao cho
x(x + 1)(x + 2)(x + 3)=24
Theo dõi (0) 3 Trả lời -


Tìm 2 số biết rằng bốn lần sô thứ hai cộng với năm lần số thứ nhất bằng 18040 và ba lần số thứ nhất hơn hai lần số thứ hai là 2002.
bởi Thành Lâm
 16/03/2020
16/03/2020
Tìm 2 số biết rằng bốn lần sô thứ hai cộng với năm lần sô thứ nhất bằng 18040 và ba lần sô thứ nhất hơn hai lần sô thứ hai là 2002.
Theo dõi (0) 2 Trả lời -


Tìm tọa độ giao điểm A, B của hai đồ thị và tính diện tích ∆OAB
bởi Nguyễn Trần Hoài Phương
 16/03/2020
16/03/2020
Trên mặt phẳng tọa độ Oxy cho parabol y=x^2 và d y=-x+6
Gọi A, B là giáo điểm của hai đồ đồ thị. Tìm tọa độ A, B và tính diện tích ∆OAB
Theo dõi (0) 0 Trả lời -


Chứng tỏ P và d luôn cắt nhau tại 2 điểm phân biệt ; Tìm m để diện tích ∆OAB bằng 12
bởi Nguyễn Trần Hoài Phương
 16/03/2020
16/03/2020
Cho parabol y=1/2x^2 và (d) y=mx+2
a) Chứng tỏ P và d luôn cắt nhau tại 2 điểm phân biệt
b) Tìm m để diện tích ∆OAB bằng 12
Theo dõi (0) 0 Trả lời -


Bài tập về tiếp tuyến đường tròn
bởi Lê Minh Ngọc
 16/03/2020
16/03/2020
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC = AM
a) Chứng minh AB = BC
b) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.
2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).
a) Chứng minh OM // BC
b) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hành
c) Chứng minh COMN là hình thang cân
3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).Kẻ CH vuông góc với AB tại H
a) Chứng minh CA là phân giác góc HCM
b) Kẻ CH vuông góc Ax tại K, gọi I là giao điểm của AC và HK. Chứng minh tam giác AIO vuông
c) Chứng minh 3 điểm M, I, O thẳng hàng
Mọi người ơi giúp e vsssssssssssssss.........E hỏi mà hong ai chỉ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tất cả các giá trị của x để (4a) /b <=x/((√x) -3)
bởi Phong Lan
 15/03/2020
15/03/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Cho y=(m-1)x+2m+1 (d). Tìm m để khoảng cách từ gốc tọa độ đến (d) đạt GTLN
bởi Bùi Mai Phương
 15/03/2020
15/03/2020
Cho y=(m-1)x+2m+1 (d)
Tìm m để khoảng cách từ gốc tọa độ đến (d) đạt GTLN
Theo dõi (0) 0 Trả lời -


Xác định vị trí tương đối của hai đường tròn ?
bởi Tran Duc Anh
 14/03/2020
14/03/2020
Cho hai đường tròn(O; R) và (O’; R’) biết R = 5cm, R’ = 3cm và OO’ = 6cm. Vị trí tương đối của hai đường tròn là:
A. cắt nhau
B. ngoài nhau
C. tiếp xúc ngoài
D. tiếp xúc trong
Theo dõi (0) 5 Trả lời -


Trắc nhiệm hệ phương trình
bởi Tran Duc Anh
 14/03/2020
14/03/2020
Phương trình nào dưới đây có thể kết hợp với phương trình 2x - y = 5 để được một hệ phương trình vô nghiệm?
1 điểm
A. y = 2x + 5
B. 0.x - y = 5
C. 4x - 5y = 10
D. 2x – 0.y = 5
Theo dõi (0) 1 Trả lời -


Cho A= x2 - 2(m+1)x + m - 1. Chứng minh phương trình luôn luôn có nghiệm phân biệt với mọi m
bởi Nguyễn Việt Tiến
 14/03/2020
14/03/2020
Cho A= x2 - 2(m+1)x + m - 1
a) Chứng minh phương trình luôn luôn có nghiệm phân biệt với mọi m ;
b) Chứng minh rằng biểu thức :
A=x1(1-x1) + X2(1 - x2) trong đó x1,x2 là các nghiệm của phương trình đã cho không phụ thuộc vào m
Theo dõi (0) 1 Trả lời -


Bốn lần số thứ hai cộng lại với năm lần số thứ nhất bằng 18040 và ba lần số thứ nhất hơn hai lần số thứ hai là 2002. Tìm hai số đó?
bởi Thành Lâm
 14/03/2020
14/03/2020
Tìm hai số biết rằng bốn lần số thứ hai cộng lại với năm lần số thứ nhất bằng 18040 và ba lần số thứ nhất hơn hai lần số thứ hai là 2002
Theo dõi (1) 6 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức
bởi Nguyễn Việt Tiến
 13/03/2020
13/03/2020
tìm giá trị nhỏ nhất của biểu thức
S=
Theo dõi (0) 2 Trả lời -


Hai đội công nhân cùng làm một đoạn đường trong 24 ngày thì xong. Mỗi ngày, phần việc đội A làm gấp rưỡi đội B. Hỏi nếu làm một mình mỗi độilàm việc xong đoạn đường trong bao lâu?
bởi Đặng Kiệt
 12/03/2020
12/03/2020
bài 1 Hai đội công nhân cùng làm một đoạn đường trong 24 ngày thì xong.
Mỗi ngày, phần việc đội A làm gấp rưỡi đội B. Hỏi nếu làm một mình mỗi đội
làm việc xong đoạn đường trong bao lâu.bài 2:Một xe tải đi từ A đến B dài 189 km. Sau khi xe tải đi được 1 giờ thì một
chiếc xe khách đi B đến A và gặp xe tải sau khi đi được 1 giờ 48 phút. Tính
vận tốc mỗi xe, biết rằng mỗi giờ xe khách đi nhanh hơn xe tải 13 km.Theo dõi (0) 5 Trả lời -


Giải phương trình 2(x^2-5)=x
bởi Nguyễn Lý Thùy Trâm
 09/03/2020
Làm giúp mình câu 4,5,6 nhà. Cảm ơn mọi người nhiều lắm.
09/03/2020
Làm giúp mình câu 4,5,6 nhà. Cảm ơn mọi người nhiều lắm. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình |5-2x| =|1-x|
bởi Phúc Lâmm
 03/03/2020
03/03/2020
|5-2x| =|1-x|
Theo dõi (0) 0 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức A=1/(x^2+y^2)+1/xy biết x, y dương thỏa mãn x+y=1
bởi Hằng Lê Thị
 03/03/2020
Tìm min
03/03/2020
Tìm min Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


giải hệ pt 2(x-2)+3(1+y)=-2
3(x-2)-2(x+1)=-3
Theo dõi (0) 0 Trả lời -


Cho hệ phương trình
x+ay=3
ax-y=2
a, giải hệ phương trình khi a=2
b, tìm điều kiện của a để hệ phương trình có nghiệm duy nhất thỏa mãn x+y>0
c, tìm giá trị của a để hệ phương trình có nghiệm (x, y) thỏa mãn x=√2y
Ae giúp mik nhanh vs mai mik nộp bài rồi
Theo dõi (1) 2 Trả lời -


Viết nghiệm tổng quát của phương trình 3x - y = 2
bởi Nguyễn Thư
 27/02/2020
27/02/2020
Hãy viết nghiệm tổng quát và biểu diễn tập nghiệm của các pt sau:
a. 3x - y = 2
b. 2x + y = 5
c. 4x + 0y = -2
d. 0x + 2y = -4
Theo dõi (1) 2 Trả lời -


Tìm tọa độ giao điểm của hai đường thẳng
và
Theo dõi (1) 1 Trả lời -


Chứng minh SA^2 = SC.SB biết đường tròng (O) đường kính AB, trên tiếp tuyến tại A của (O) lấy điểm S
bởi Nguyen Huynhf Quoc Quoc Thanh
 24/02/2020
24/02/2020
cho đường tròng (o) đường kính AB, trên tiếp tuyến tại A của (o) lấy điểm S (S khác A), SB cắt dwuongf tròn (o) tại điểm thứ 2 là C. CMR: SA^2 = SC.SB
Theo dõi (0) 2 Trả lời -


Tìm giá trị của m để đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 1/2
bởi Nguyễn Thành Minh
 23/02/2020
23/02/2020
Cho hàm số bậc nhất: y= (m2 +1) x + m có đồ thị là đường thẳng d
a) Tìm giá trị của m để đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 1/2
b) Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1/căn 5
Theo dõi (0) 0 Trả lời -


Tìm GTNN của biểu thức B=x+ 2/x -(2√x +1)/x+2 + 2019
bởi Nhinh Nguyễn
 22/02/2020
22/02/2020
Cho x>0, tìm GTNN của biểu thức:
B=x+ 2/x -(2√x +1)/x+2 + 2019
Theo dõi (0) 1 Trả lời -


Chứng minh các đường thẳng d1:3x+y=7; d2: -2x+y=-3;d3:y=3x-5 cùng đi qua 1 điểm
bởi Tắc kè Hoa
 19/02/2020
19/02/2020
chứng minh các đường thẳng d1:3x+y=7; d2: -2x+y=-3;d3:y=3x-5 cùng đi qua 1 điểm
Theo dõi (0) 1 Trả lời -


Tính số tiền bà An và bà Bình gửi tiết kiệm
bởi Dương Anh Thư
 19/02/2020
19/02/2020
Bà An và bà Bình gửi tiết kiệm vào hai ngân hàng với tổng số tiền là 600 triệu . Bà An gửi ngân hàng A với lãi suất 7% một năm , bà Bình gửi ngân hàng B với lãi suất 6,5% một năm . Sau 1 năm tổng số tiền lãi hai bà nhận được là 40 triệu đồng . Hỏi mỗi bà gửi bao nhiêu tiền
Giúp em với ạ!
Theo dõi (0) 2 Trả lời -


Giải phương trình x^2-5x+m=0 khi m=6
bởi Miinh Nguyen
 18/02/2020
18/02/2020
Cho Phương Trình : x^2-5x+m=0
a) Giải Phương Trình trên khi m=6
b) Tìm m để phương trình trên có 2 nghiệm x1, x2 thõa mãn : |x1 - x2|=3
Theo dõi (0) 2 Trả lời -


Ah cho hpt ( a - 1)x +y= a và x+ ( a - 1 )y = 2 tìm a để hot có nghiệm duy nhất thỏa mãn x +y = -1
Theo dõi (0) 0 Trả lời -


Hai người làm chung một công việc thì xong trong 4h .Nếu người thứ nhất làm trong 2 giờ và giời thứ 2 làm trong 3h thì được 7/12 công việc .Hỏi nếu mỗi người làm riêng thì trong bao lâu xong công việc Giúp mình với!
Theo dõi (1) 6 Trả lời -


Chứng minh đường thẳng y=mx+2(m+1) luôn đi qua một điểm cố định với mọi giá trị của m
bởi Tang Luân
 20/12/2019
20/12/2019
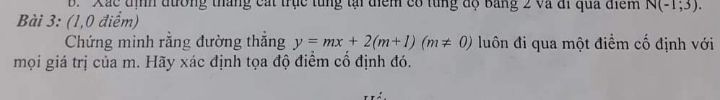 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cm bất đẳng thức 1/2.3^2+1/3.4^2+...+1/n(n+1)^2 < 1/4
bởi Minh Hoàng
 19/07/2019
Mọi ng giúp e với ạ
19/07/2019
Mọi ng giúp e với ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh a^3/(a^2 + b^2) + b^3/(b^2 + c^2) + c^3/(c^2 + a^2) ≥ (a + b + c)/2
bởi Chỉ Một Từ Không
 09/07/2019
09/07/2019
Cho a, b, c > 0. Chứng minh a^3/(a^2 + b^2) + b^3/(b^2 + c^2) + c^3/(c^2 + a^2) ≥ (a + b + c)/2
Theo dõi (0) 4 Trả lời -


Giải phương trình nghiệm nguyên x^x-3=65y
bởi Linh Trần
 09/07/2019
09/07/2019
Giải pt nghiệm nguyên
2x-3=65y
Theo dõi (0) 2 Trả lời -


Giải pt nghiệm nguyên
x2=y2+
(x,y là số tự nhiên)
Theo dõi (0) 3 Trả lời -


Giải phương trình nghiệm nguyên z^2002-2000y^2001=2003
bởi Linh Trần
 08/07/2019
08/07/2019
Giải ptnn
z2002-2000y2001=2003
Theo dõi (1) 2 Trả lời -


Chứng minh bất đẳng thức a^2b^2(a^2+b^2) < = 2
bởi do thi nhu y
 08/07/2019
08/07/2019
cho a,b>0, a+b=2 chứng minh:
a2b2(a2+b2)<=2
Theo dõi (0) 1 Trả lời -


cho a,b,c>0 và abc=1 tìm Max T= (a/b4+c4+a) + (c/a4+b4+c)+(b/c4+a4+b)
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 65 trang 64 SGK Toán 9 Tập 2
Bài tập 66 trang 64 SGK Toán 9 Tập 2
Bài tập 68 trang 63 SBT Toán 9 Tập 2
Bài tập 69 trang 63 SBT Toán 9 Tập 2
Bài tập 70 trang 63 SBT Toán 9 Tập 2
Bài tập 71 trang 63 SBT Toán 9 Tập 2
Bài tập 72 trang 63 SBT Toán 9 Tập 2
Bài tập 73 trang 63 SBT Toán 9 Tập 2
Bài tập 73 trang 63 SBT Toán 9 Tập 2
Bài tập 74 trang 63 SBT Toán 9 Tập 2
Bài tập 74 trang 63 SBT Toán 9 Tập 2
Bài tập 4.1 trang 64 SBT Toán 9 Tập 2
Bài tập 4.2 trang 64 SBT Toán 9 Tập 2
Bài tập 4.3 trang 64 SBT Toán 9 Tập 2






