Phần hướng dẫn giải bài tập SGK Toán 9 Chương 4 Bài 9 Ôn tập chương Phương trình bậc hai một ẩn sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9.
-
Câu hỏi 1 trang 60 SGK Toán 9 Tập 2
Hãy vẽ đồ thị của các hàm số \(y = 2x^2, y = -2x^2.\) Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số \(y = ax^2\) đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số \(y = ax^2\) có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
-
Câu hỏi 2 trang 60 SGK Toán 9 Tập 2
Đối với phương trình bậc hai \(ax^2 + bx + c = 0 (a ≠ 0),\) hãy viết công thức tính \(Δ, Δ'.\)
Khi nào thì phương trình vô nghiệm?
Khi nào phương trình có hai nghiệm phân biệt? Viết công thức nghiệm.
Khi nào phương trình có nghiệm kép? Viết công thức nghiệm.
Vì sao khi a và c trái dấu thì phương trình có hai nghiệm phân biệt?
-
Câu hỏi 3 trang 61 SGK Toán 9 Tập 2
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai \(ax^2 + bx + c = 0 (a ≠ 0),\)
Nêu điều kiện để phương trình \(ax^2 + bx + c = 0 (a ≠ 0),\) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình \(1954x^2 + 21x – 1975 = 0\)
Nêu điều kiện để phương trình \(ax^2 + bx + c = 0 (a ≠ 0),\) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình \(2005x^2 + 104x – 1901 = 0\)
-
Câu hỏi 4 trang 61 SGK Toán 9 Tập 2
Nêu cách tìm hai số, biết tổng S và tích P của chúng.
Tìm hai số u và v trong mỗi trường hợp sau:
\(\begin{array}{l}
a)\left\{ \begin{array}{l}
u + v = 3\\
uv = - 8
\end{array} \right.\\
b)\left\{ \begin{array}{l}
u + v = 5\\
uv = 10
\end{array} \right.
\end{array}\) -
Câu hỏi 5 trang 61 SGK Toán 9 Tập 2
Nêu cách giải phương trình trùng phương \(ax^4 + bx^2 + c = 0,(a ≠ 0)\)
-
Bài tập 54 trang 63 SGK Toán 9 Tập 2
Vẽ đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = - {1 \over 4}{x^2}\) trên cùng một hệ trục tọa độ
a) Qua điểm \(B(0; 4)\) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) tại hai điểm M và M’. Tìm hoành độ của M và M’.
b) Tìm trên đồ thị của hàm số \(\displaystyle y = - {1 \over 4}{x^2}\) điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:
- Ước lượng trên hình vẽ:
- Tính toán theo công thức.
-
Bài tập 55 trang 63 SGK Toán 9 Tập 2
Cho phương trình: x2 - x - 2 = 0.
a) Giải phương trình.
b) Vẽ hai đồ thị y = x2 và y = x + 2 trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
-
Bài tập 56 trang 63 SGK Toán 9 Tập 2
Giải các phương trình:
a) 3x4 – 12x2 + 9 = 0;
b) 2x4 + 3x2 – 2 = 0;
c) x4 + 5x2 + 1 = 0.
-
Bài tập 57 trang 63 SGK Toán 9 Tập 2
Giải các phương trình:
a) \(5{{\rm{x}}^2} - 3{\rm{x}} + 1 = 2{\rm{x}} + 11\)
b) \({{{x^2}} \over 5} - {{2{\rm{x}}} \over 3} = {{x + 5} \over 6}\)
c) \({x \over {x - 2}} = {{10 - 2{\rm{x}}} \over {{x^2} - 2{\rm{x}}}}\)
d) \({{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} - 1}}\)
e) \(2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right)\)
f) \({x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right)\)
-
Bài tập 58 trang 63 SGK Toán 9 Tập 2
Giải các phương trình
a) \(1,2{{\rm{x}}^3} - {x^2} - 0,2{\rm{x}} = 0\)
b) \(5{{\rm{x}}^3} - {x^2} - 5{\rm{x}} + 1 = 0\)
-
Bài tập 59 trang 63 SGK Toán 9 Tập 2
Giải các phương trình bằng cách đặt ẩn phụ:
a) \(2{\left( {{x^2} - 2{\rm{x}}} \right)^2} + 3\left( {{x^2} - 2{\rm{x}}} \right) + 1 = 0\)
b) \({\left( {x + {1 \over x}} \right)^2} - 4\left( {x + {1 \over x}} \right) + 3 = 0\)
-
Bài tập 60 trang 64 SGK Toán 9 Tập 2
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a) \(12{{\rm{x}}^2} - 8{\rm{x}} + 1 = 0;{x_1} = {1 \over 2}\)
b) \(2{{\rm{x}}^2} - 7{\rm{x}} - 39 = 0;{x_1} = - 3\)
c) \({x^2} + x - 2 + \sqrt 2 = 0;{x_1} = - \sqrt 2 \)
d) \({x^2} - 2m{\rm{x}} + m - 1 = 0;{x_1} = 2\)
-
Bài tập 61 trang 64 SGK Toán 9 Tập 2
Tìm hai số u và v trong mỗi trường hợp sau:
a) \(u + v = 12\); \(uv = 28\) và \(u > v\)
b) \(u + v = 3; uv = 6\)
-
Bài tập 62 trang 64 SGK Toán 9 Tập 2
Cho phương trình \(7x^2 + 2(m – 1)x – m^2= 0\)
a) Với giá trị nào của \(m\) thì phương trình có nghiệm?
b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo \(m\).
-
Bài tập 63 trang 64 SGK Toán 9 Tập 2
Sau hai năm, số dân của một thành phố tăng từ \(2 000 000\) người lên \(2 020 050\) người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?
-
Bài tập 64 trang 64 SGK Toán 9 Tập 2
Bài toán yêu cầu tìm tích của một số dương với một số lớn hơn nó 2 đơn vị, nhưng bạn Quân nhầm đầu bài lại tính tích của một số dương với một số bé hơn nó 2 đơn vị. Kết quả của bạn Quân là 120. Hỏi nếu làm đúng đầu bài đã cho thì kết quả phải là bao nhiêu?
-
Bài tập 65 trang 64 SGK Toán 9 Tập 2
Một xe lửa đi từ Hà Nội vào Bình Sơn (Quảng Ngãi). Sau đó 1 giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với vận tốc lớn hơn vận tốc của xe lửa thứ nhất là 5km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng đường. Tìm vận tốc của mỗi xe, giả thiết rằng quãng đường Hà Nội – Bình Sơn dài 900km.
-
Bài tập 66 trang 64 SGK Toán 9 Tập 2
Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.
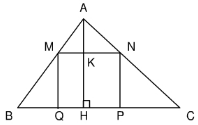
-
Bài tập 67 trang 63 SBT Toán 9 Tập 2
Cho hai hàm số: \(y = 2x - 3\) và \(y = - {x^2}\)
a) Vẽ đồ thị hai hàm số này trong cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị.
c) Kiểm nghiệm rằng tọa độ của mỗi giao điểm đều là nghiệm chung của hai phương trình hai ẩn y = 2x – 3 và \(y = - {x^2}\)
-
Bài tập 68 trang 63 SBT Toán 9 Tập 2
Giải các phương trình:
a) \(3{x^2} + 4\left( {x - 1} \right) = {\left( {x - 1} \right)^2} + 3\)
b) \({x^2} + x + \sqrt 3 = \sqrt 3 x + 6\)
c) \({{x + 2} \over {1 - x}} = {{4{x^2} - 11x - 2} \over {\left( {x + 2} \right)\left( {x - 1} \right)}}\)
d) \({{{x^2} + 14x} \over {{x^3} + 8}} = {x \over {x + 2}}\)
-
Bài tập 69 trang 63 SBT Toán 9 Tập 2
Giải các phương trình trùng phương
a) \({x^4} + 2{x^2} - x + 1 = 15{x^2} - x - 35\)
b) \(2{x^4} + {x^2} - 3 = {x^4} + 6{x^2} + 3\)
c) \(3{x^4} - 6{x^2} = 0\)
d) \(5{x^4} - 7{x^2} - 2 = 3{x^4} - 10{x^2} - 3\)
-
Bài tập 70 trang 63 SBT Toán 9 Tập 2
Giải các phương trình sau bằng phương pháp đặt ẩn phụ:
a) \({\left( {{x^2} - 2x} \right)^2} - 2{x^2} + 4x - 3 = 0\)
b) \(3\sqrt {{x^2} + x + 1} - x = {x^2} + 3\)
-
Bài tập 71 trang 63 SBT Toán 9 Tập 2
Cho phương trình:
\({x^2} - 2\left( {m + 1} \right)x + {m^2} + m - 1 = 0\)
a) Tìm các giá trị của m để phương trình có nghiệm.
b) Trong trường hợp phương trình có nghiệm là x1, x2 hãy tính theo m:
\({x_1} + {x_2};{x_1}{x_2};{x_1}^2 + {x_2}^2\)
-
Bài tập 72 trang 63 SBT Toán 9 Tập 2
Tìm hai số biết tổng của chúng bằng \(10\) và tích của chúng bằng \(-10\).
-
Bài tập 73 trang 63 SBT Toán 9 Tập 2
Một đội thợ mỏ phải khai thác \(216\) tấn than trong một thời hạn nhất định. Ba ngày đầu mỗi ngày đội khai thác theo đúng định mức. Sau đó mỗi ngày họ đều khai thác vượt định mức \(8\) tấn. Do đó họ khai thác được \(232\) tấn và xong trước thời hạn một ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai thác bao nhiêu tấn than?
-
Bài tập 73 trang 63 SBT Toán 9 Tập 2
Một đội thợ mỏ phải khai thác \(216\) tấn than trong một thời hạn nhất định. Ba ngày đầu mỗi ngày đội khai thác theo đúng định mức. Sau đó mỗi ngày họ đều khai thác vượt định mức \(8\) tấn. Do đó họ khai thác được \(232\) tấn và xong trước thời hạn một ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai thác bao nhiêu tấn than?
-
Bài tập 74 trang 63 SBT Toán 9 Tập 2
Khoảng cách giữa hai bến sông \(A\) và \(B\) là \(30km\). Một ca nô đi từ \(A\) đến \(B\), nghỉ \(40\) phút ở \(B\) rồi lại trở về bến \(A\). Thời gian kể từ lúc đi đến lúc trở về đến \(A\) là \(6\) giờ. Tính vận tốc của ca nô khi nước yên lặng, biết rằng vận tốc của dòng nước là \(3km/h\).
-
Bài tập 74 trang 63 SBT Toán 9 Tập 2
Khoảng cách giữa hai bến sông \(A\) và \(B\) là \(30km\). Một ca nô đi từ \(A\) đến \(B\), nghỉ \(40\) phút ở \(B\) rồi lại trở về bến \(A\). Thời gian kể từ lúc đi đến lúc trở về đến \(A\) là \(6\) giờ. Tính vận tốc của ca nô khi nước yên lặng, biết rằng vận tốc của dòng nước là \(3km/h\).
-
Bài tập 4.1 trang 64 SBT Toán 9 Tập 2
Cho hàm số \(y = - 3{x^2}\). Khẳng định nào sau đây là đúng?
A) Khi \(0 < x < 15,\) hàm số đồng biến
B) Khi \(-1 < x < 1,\) hàm số đồng biến
C) Khi \(-15 < x < 0,\) hàm số đồng biến
D) Khi \(-15 < x < 1,\) hàm số đồng biến
-
Bài tập 4.2 trang 64 SBT Toán 9 Tập 2
Muốn tìm hai số khi biết tổng của chúng bằng \(S,\) tích của chúng bằng \(P\) thì ta giải phương trình nào sau đây?
A) \({x^2} + Sx + P = 0\)
B) \({x^2} - Sx + P = 0\)
C) \({x^2} - Sx - P = 0\)
D) \({x^2} + Sx - P = 0\)
-
Bài tập 4.3 trang 64 SBT Toán 9 Tập 2
Giải các phương trình:
a) \(\displaystyle {x^3} + 4{x^2} + x - 6 = 0\)
b) \(\displaystyle {x^3} - 2{x^2} - 5x + 6 = 0\)
c) \(\displaystyle 2{x^4} + 2\sqrt 2 {x^3} + \left( {1 - 3\sqrt 2 } \right){x^2} \)\(\displaystyle - 3x - 4 = 0\)
d) \(\displaystyle \left( {2{x^2} + 7x - 8} \right)\left( {2{x^2} + 7x - 3} \right) \)\(\displaystyle - 6 = 0\)
-
Bài tập 4.4 trang 64 SBT Toán 9 Tập 2
Cho phương trình: \({x^2} + px + 1 = 0\) có hai nghiệm. Xác định \(p\) biết rằng tổng các bình phương của hai nghiệm bằng \(254.\)
-
Bài tập 4.5 trang 64 SBT Toán 9 Tập 2
Cho phương trình: \(\displaystyle {x^4} - 13{x^2} + m = 0\). Tìm các giá trị của \(\displaystyle m\) để phương trình:
a) Có 4 nghiệm phân biệt
b) Có 3 nghiệm phân biệt
c) Có 2 nghiệm phân biệt
d) Có một nghiệm
e) Vô nghiệm.






