Giải bài 17 tr 11 sách GK Toán 8 Tập 1
Chứng minh rằng:
\({(10a + 5)^2} = 100a.(a + 1) + 25\)
Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.
Áp dụng để tính: 252, 352, 652, 752.
Hướng dẫn giải chi tiết
Với bài tập 17 này, ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhẩm bình phương của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng;
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
-- Mod Toán 8 HỌC247
-


Viết biểu thức \({x^3}\; + {\rm{ }}3{x^2}\; + {\rm{ }}3x{\rm{ }} + {\rm{ }}1\) dưới dạng lập phương của một tổng.
bởi Naru to
 20/01/2021
Theo dõi (0) 2 Trả lời
20/01/2021
Theo dõi (0) 2 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính 56.64
bởi Mai Vi
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -


Tính ( x - 2 )( x + 2 ).
bởi Goc pho
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -


Viết biểu thức \(4{x^2}\; - {\rm{ }}4x{\rm{ }} + {\rm{ }}1\) dưới dạng bình phương của một hiệu
bởi Nguyễn Hiền
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Viết biểu thức \({x^2}\; + {\rm{ }}4x{\rm{ }} + {\rm{ }}4\) dưới dạng bình phương của một tổng.
bởi hi hi
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Nhà bạn Minh và bạnA n cùng trồng bắp cải trên hai mảnh vườn hình vuông khác nhau. Các cây bắp cải được cách đều nhau. Do vườn nhà bạn Minh lớn hơn nên số cây bắp cải trồng được lớn hơn vườn nhà bạn An là 211 cây. Hỏi nhà bạn Minh đã trồng bao nhiêu cây bắp cải?
bởi My Hien
 14/01/2021
14/01/2021
A. 106 cây
B. 11025 cây
C. 11236 cây
D. 105 cây
Theo dõi (0) 1 Trả lời -


Biểu thức (a – b – c)^2 bằng
bởi Nguyễn Thị Trang
 15/01/2021
15/01/2021
Biểu thức (a – b – c)2 bằng
A. a2 + b2 + c2 – 2(bc + ac + ab)
B. a2 + b2 + c2 + bc – ac – 2ab
C. a2 + b2 + c2 + 2(bc – ac – ab)
C. a2 + b2 + c2 + 2(bc – ac – ab)
Theo dõi (0) 1 Trả lời -


Biểu thức (a + b + c)^2 bằng
bởi Phung Hung
 15/01/2021
15/01/2021
Biểu thức (a + b + c)2 bằng
A. a2 + b2 + c2 + 2(ab + ac + bc)
B. a2 + b2 + c2 + bc + ac + 2ab
C. a2 + b2 + c2 + ab + ac + bc
D. a2 + b2 + c2 – 2(ab + ac + bc)
Theo dõi (0) 1 Trả lời -


Giá trị nhỏ nhất của biểu thức I là
bởi Lê Gia Bảo
 14/01/2021
14/01/2021
Giá trị nhỏ nhất của biểu thức I = (x2 + 4x + 5)(x2 + 4x + 6) + 3 là
A. 4
B. 5
C. 3
D. 2
Theo dõi (0) 1 Trả lời -


Biểu thức J có giá trị nhỏ nhất khi
bởi Nguyễn Anh Hưng
 14/01/2021
14/01/2021
A. -12
B. 5
C. 12
D. -5
Theo dõi (0) 1 Trả lời -


Biểu thức K có giá trị nhỏ nhất khi
bởi Anh Nguyễn
 14/01/2021
14/01/2021
Biểu thức K = x2 – 6x + y2 – 4y + 6 có giá trị nhỏ nhất là
A. 6
B. 1
C. -7
D. 7
Theo dõi (0) 1 Trả lời -


Biểu thức F = x^2 – 12x +34 đạt giá trị nhỏ nhất khi
bởi Trung Phung
 14/01/2021
14/01/2021
A. x = 6
B. x = -6
C. x = 8
D. x = 2
Theo dõi (0) 1 Trả lời -


Biểu thức E = x^2 – 20x +101 đạt giá trị nhỏ nhất khi
bởi Truc Ly
 14/01/2021
14/01/2021
A. x = 9
B. x = 10
C. x = 11
D.x = 12
Theo dõi (0) 1 Trả lời -


Tìm giá trị lớn nhất của biểu thức Q
bởi Mai Thuy
 14/01/2021
14/01/2021
Tìm giá trị lớn nhất của biểu thức Q = 8 – 8x – x2
A. 8
B. 11
C. -4
D. 24
Theo dõi (0) 1 Trả lời -


Cho T = -9x^2 + 6x – 5. Chọn khẳng định đúng
bởi Lan Anh
 14/01/2021
14/01/2021
A. T < -4
B. T ≥ -4
C. T > -4
D.T ≤ -4
Theo dõi (0) 1 Trả lời -


Chọn khẳng định đúng. Cho P = -4x^2 + 4x – 2
bởi Nguyễn Lệ Diễm
 14/01/2021
14/01/2021
A. P ≤ -1
B. P > -1
C. P > 0
D. P ≤ - 2
Theo dõi (0) 1 Trả lời -


Chọn câu đúng về giá trị các biểu thức sau
bởi na na
 15/01/2021
15/01/2021
Chọn câu đúng về giá trị các biểu thức sau mà không tính cụ thể
A = 1 + 15(42 + 1)(44 + 1)(48 + 1) và B = (43)5 + (45)3
A. A = B + 2
B. B = 2A
C. A = 2B
D. A = B
Theo dõi (0) 1 Trả lời -


So sánh M và N
bởi Phan Thị Trinh
 15/01/2021
15/01/2021
So sánh M = 232 và N = (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
A. M > N
B. M < N
C. M = N
D. M = N – 1
Theo dõi (0) 1 Trả lời -


A. A= B
B. A ≥ B
C. A > B
D.A < B
Theo dõi (0) 1 Trả lời -


So sánh A = 2016.2018.a và B = 2017.a (với a > 0)
bởi trang lan
 15/01/2021
15/01/2021
A. A = B
B. A < B
C. A > B
D. A ≥ B
Theo dõi (0) 1 Trả lời -


Tìm x biết (3x – 1)2 + 2(x + 3)2 + 11(1 + x)(1 – x) = 6
A. x = -4
B. x = 4
C. x = -1
D. x = -2
Theo dõi (0) 1 Trả lời -


Tìm x biết (x – 6)(x + 6) – (x + 3)^2 = 9
bởi Spider man
 15/01/2021
15/01/2021
A. x = -9
B. x = 9
C. x = 1
D. x = -6
Theo dõi (0) 1 Trả lời -


Tìm mối quan hệ giữa M và N
bởi Huong Duong
 15/01/2021
15/01/2021
Cho M = 4(x + 1)2 + (2x + 1)2 – 8(x – 1)(x + 1) – 12x và N = 2(x – 1)2 – 4(3 + x)2 + 2x(x + 14).
Tìm mối quan hệ giữa M và N
A. 2N – M = 60
B. 2M – N = 60
C. M> 0, N < 0
D. M > 0, N > 0
Theo dõi (0) 1 Trả lời -


A. B < 12
B. B > 13
C. 12 < B< 14
D. 11 < B < 13
Theo dõi (0) 1 Trả lời -


A. 0
B. 1
C. 19
D. – 19
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức A
bởi Phan Quân
 15/01/2021
15/01/2021
Rút gọn biểu thức A = 5(x + 4)2 + 4(x – 5)2 – 9(4 + x)(x – 4), ta được
A. 342
B. 243
C. 324
D. -324
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức A = (3x – 1)^2 – 9x(x + 1) ta được
bởi Nguyễn Hiền
 15/01/2021
15/01/2021
A. -15x + 1
B. 1
C. 15x + 1
D. – 1
Theo dõi (0) 1 Trả lời -


Chọn câu đúng
bởi bach hao
 14/01/2021
14/01/2021
A. 4 – (a + b)2 = (2 + a + b)(2 – a + b)
B. 4 – (a + b)2 = (4 + a + b)(4 – a – b)
C. 4 – (a + b)2 = (2 + a – b)(2 – a + b)
D. 4 – (a + b)2 = (2 + a + b)(2 – a – b)
Theo dõi (0) 1 Trả lời -


Chọn câu đúng
bởi Nguyễn Xuân Ngạn
 15/01/2021
15/01/2021
A. (c + d)2 – (a + b)2 = (c + d + a + b)(c + d – a + b)
B. (c – d)2 – (a + b)2 = (c – d + a + b)(c – d – a + b)
C. (a + b + c – d)(a + b – c + d) = (a + b)2 – (c – d)2
D. (c – d)2 – (a – b)2 = (c – d + a – b)(c – d – a – b)
Theo dõi (0) 1 Trả lời -


A. (5x – 2y)2
B. (2x – 5y)2
C. (25x – 4y)2
D. (5x + 2y)2
Theo dõi (0) 1 Trả lời -


Khai triển (3x – 4y)^2 ta được
bởi Bánh Mì
 15/01/2021
15/01/2021
A. 9x2 – 24xy + 16y2
B. 9x2 – 12xy + 16y2
C. 9x2 – 24xy + 4y2
D. 9x2 – 6xy + 16y2
Theo dõi (0) 1 Trả lời -


Khai triển 4x^2 – 25y^2 theo hằng đẳng thức ta được
bởi Hong Van
 14/01/2021
14/01/2021
A. (4x – 5y)(4x + 5y)
B. (4x – 25y)(4x + 25y)
C. (2x – 5y)(2x + 5y)
D. (2x – 5y)2
Theo dõi (0) 1 Trả lời -


Chọn câu sai.
bởi Hoai Hoai
 14/01/2021
14/01/2021
A. (x + 2y)2 = x2 + 4xy + 4y2
B. (x – 2y)2 = x2 – 4xy + 4y2
C. (x – 2y)2 = x2 – 4y2
D. (x – 2y)(x + 2y) = x2 – 4y2
Theo dõi (0) 1 Trả lời -


Chọn câu sai.
bởi Lê Văn Duyệt
 14/01/2021
14/01/2021
A. (x + y)2 = (x + y)(x + y)
B. x2 – y2 = (x + y)(x – y)
C. (-x – y)2 = (-x)2 – 2(-x)y + y2
D. (x + y)(x + y) = y2 – x2
Theo dõi (0) 1 Trả lời -


Chọn câu đúng.
bởi A La
 14/01/2021
14/01/2021
A. (A – B)(A + B) = A2 + 2AB + B2
B. (A + B)(A – B) = A2 – B2
C. (A + B)(A – B) = A2 – 2AB + B2
D. (A + B)(A – B) = A2 + B2
Theo dõi (0) 1 Trả lời -


Chọn câu đúng.
bởi Vu Thy
 14/01/2021
14/01/2021
A. (A + B)2 = A2 + 2AB + B2
B. (A + B)2 = A2 + AB + B2
C. (A + B)2 = A2 + B2
D. (A + B)2 = A2 – 2AB + B2
Theo dõi (0) 1 Trả lời -


Phân tích thành nhân tử: \(16x^2 - (x+1)^2\)
bởi Nguyen Khanh Huyen
 14/01/2021
14/01/2021
16x2 - (x+1)2
Theo dõi (0) 0 Trả lời -


Tính và thu gọn 3x^2(3x^2-2y^2)-(3x^2-2y^2)(3x^2 2y^2)
bởi Nguyễn Tư
 14/09/2020
14/09/2020
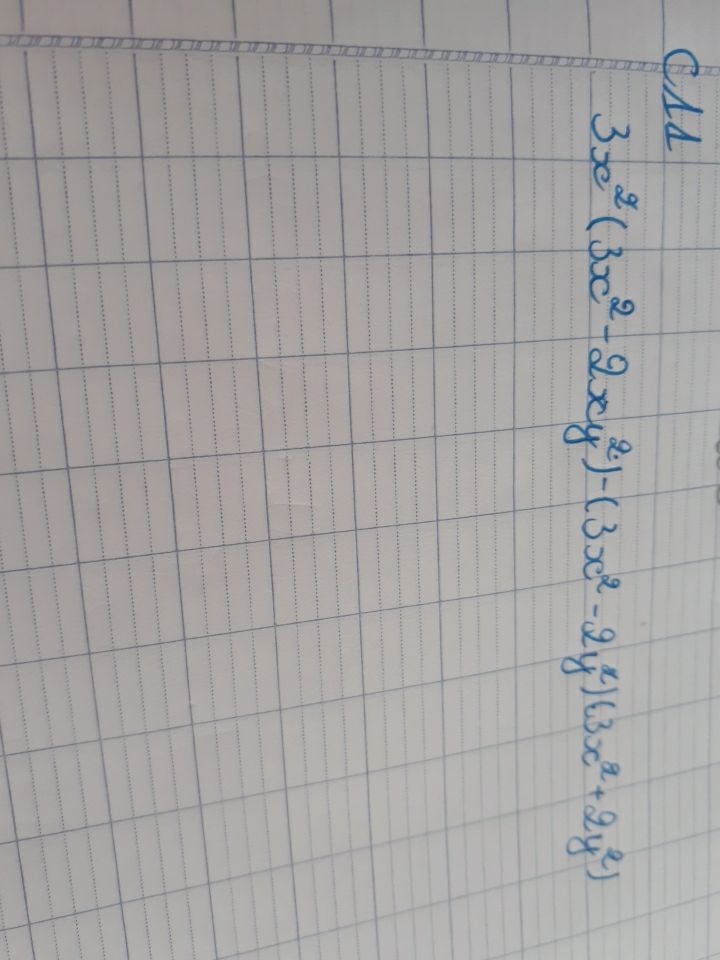 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chuyển biểu thức 9(y-1/2x)^2 + 2(y-1/2x)y + (1/9)y^2 về dạng hằng đẳng thức.
bởi Trần Huy
 09/09/2020
09/09/2020
Chuyển biểu thức sau về dạng hằng đẳng thức
1) 9(y-1/2x)^2 + 2(y-1/2x)y+1/9.y^2
2) (2x+y-1/2.z)(2x+y+1/2.z)
Theo dõi (0) 2 Trả lời -


-x²+4x-5 nhỏ hơn 0 với x thuộc z
Theo dõi (0) 1 Trả lời -


thu gọn biểu thức sau về dạng hằng đẳng thức: (;A = 4{x^2}; - { m{ }}12xy{ m{ }} + { m{ }}9{y^2})
bởi Nham Thien Huong
 08/09/2020
08/09/2020
a, A=4x2 - 12xy + 9y2
b, B=(2x2+1)(1-2x2)
c, C=x2y2+6xy3+9y4
Theo dõi (0) 3 Trả lời -


Chứng tỏ biểu thức \((x^3+x^2-3x+9)×(x+2)-(x^2+1)×(x^2+3x-2)\) không phụ thuộc vào biến x?
bởi Mun Zinn
 04/09/2020
Theo dõi (0) 1 Trả lời
04/09/2020
Theo dõi (0) 1 Trả lời -


Rút gọn rồi tính giá trị biểu thức \(A=(x + 3)^2 + ( x - 3).(x + 3)-2.(x + 2 ).(x - 4)\) với \(x ={ 1 \over 2}\)?
bởi Tình Tình
 03/09/2020
Theo dõi (0) 1 Trả lời
03/09/2020
Theo dõi (0) 1 Trả lời -


Tìm x biết \((x+1)^2-(x+1)(x-2)=0\)?
bởi Mun Cụk Súk
 03/09/2020
Theo dõi (0) 3 Trả lời
03/09/2020
Theo dõi (0) 3 Trả lời -


Viết các biểu thức \(x^2 +4 x +4\) dưới dạng bình phương của 1 tổng hoặc hiệu?
bởi Việt Trung
 01/09/2020
01/09/2020
viết các biểu thức sau dưới dạng bình phương của 1 tổng hoặc 1 hiệu
x2 +4 x +4
x2 - x + \(1 \over 4\)
Theo dõi (0) 5 Trả lời -


Tìm GTNN của các đa thức \(x^2+2x+2015\)?
bởi Vân Nguyễn
 31/08/2020
31/08/2020
Tìm GTLN (GTNN) của các đa thức sau nếu có
a) x^2+2x+2015
b)x^2-4x+7
c)-x^2-2x+17
Theo dõi (0) 1 Trả lời -


Thu gọn các biểu thức sau về hàng đẳng thức?
A= 25x2 -20xy2+4y4
B= (3x-2). ( 2+3x )
C=16+24xy3+9x2y6
D= (3x-y)2+2(y-2) (3x-y ) + (y-2)2
Theo dõi (0) 1 Trả lời -


Tìm Max
C=-x2-2y2-2xy+2x-2y-15
D=15-10x-10x^2+24xy-16y2
Theo dõi (0) 0 Trả lời -


Viết thành 1 hằng đẳng thức \(x^2+8x+16\)?
bởi gnamj
 29/08/2020
29/08/2020
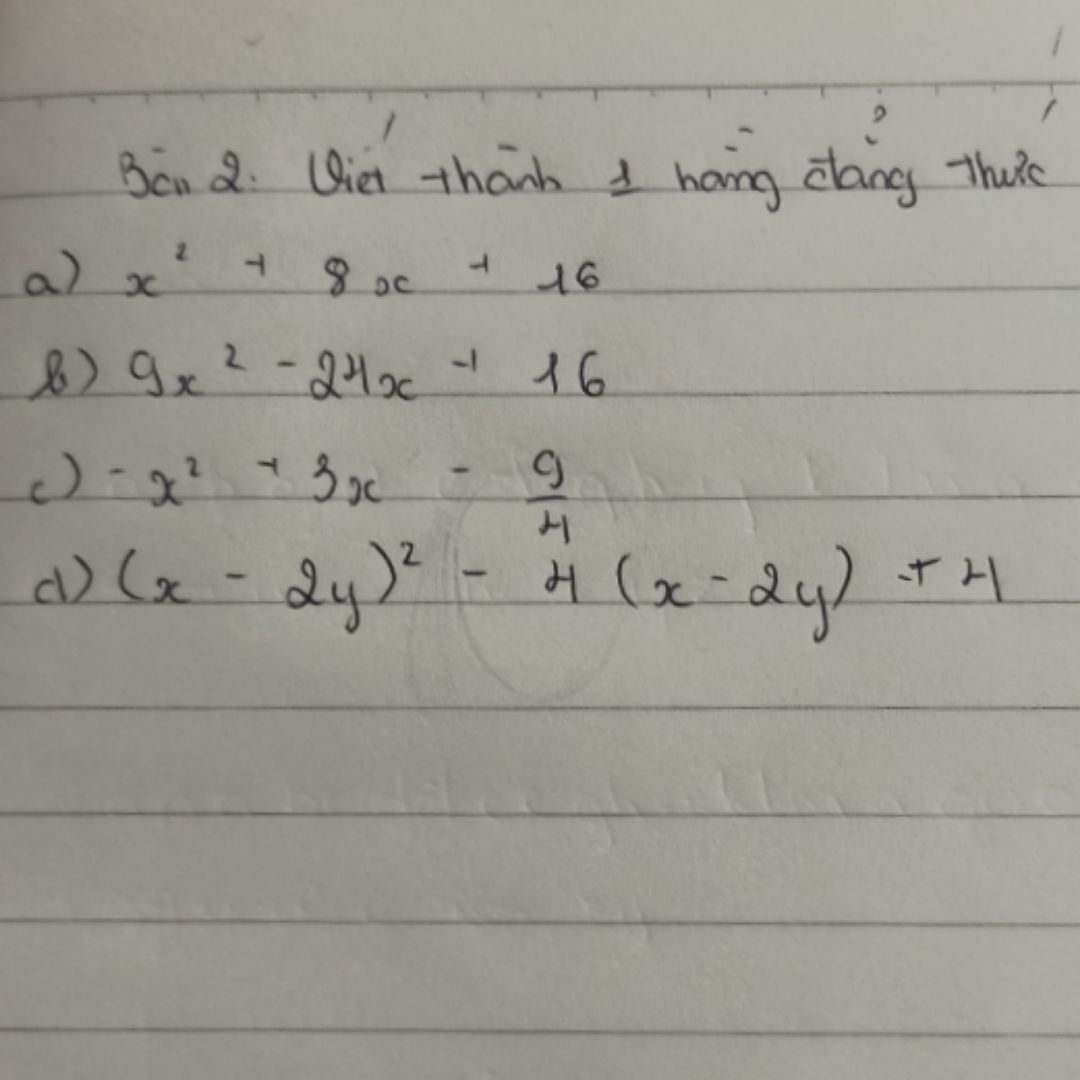 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm GTNN của \(B=x^2+y^2-xy+x-y\)?
bởi Vũ Hoàng Minh
 29/08/2020
29/08/2020
Bài 1 tìm GTNN
B=x^2+y^2-xy+x-y
C=x^2+y^2-xy-2x-3y
Bài 2 tìm GTLN
D=-2x^2-3y^2+3xy+5x-3y+4
F=2-5x^2-y^2-4xy+2x+3y
Theo dõi (0) 5 Trả lời -


Tìm GTNN của biểu thức sau: \(A=x^2-5x+12\)?
bởi Khanh Pham
 26/08/2020
Theo dõi (0) 10 Trả lời
26/08/2020
Theo dõi (0) 10 Trả lời -


Viết biểu thức sau dưới dạng bình phương của một tổng hoặc bình phương của một hiệu \(x^2+2x+1\)?
bởi Nguyễn Hạnh
 24/08/2020
24/08/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm GTNN của \(A=2x^2+ 3y^2-x +2y-1\)?
bởi Nguyễn Ken
 21/08/2020
Theo dõi (0) 0 Trả lời
21/08/2020
Theo dõi (0) 0 Trả lời -


Viết các biểu thức \(4x^2 + 4x +1\) dưới dạng bình phương của một tổng hoặc hiệu?
bởi Linh Khánh
 20/08/2020
Theo dõi (0) 9 Trả lời
20/08/2020
Theo dõi (0) 9 Trả lời -


Sử dụng hằng đẳng thức để rút gọn đa thức sau \((1+x)^2+(1-x)^2\)?
bởi Ngọc Mình Thư Nguyễn
 20/08/2020
20/08/2020
Sử dụng hằng đẳng thức để rút gọn các đa thức sau
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm GTNN của \(B = 2x^2 + 5x + 7\)?
bởi Thanh Thúy
 18/08/2020
18/08/2020
+, Tìm GTNN của:
B = 2x2 + 5x + 7
+, Tìm GTLN của:
C = 6x - x2 -12
D = -3x2 - x + 5
Theo dõi (1) 4 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức (x-3)(x+5)+4?
bởi Đỗ Minh Hằng
 17/08/2020
Theo dõi (0) 8 Trả lời
17/08/2020
Theo dõi (0) 8 Trả lời -


Tìm GTNN của \(5x^2+2y^2-4xy+20x-8y\)?
bởi oops nani
 16/08/2020
Theo dõi (0) 0 Trả lời
16/08/2020
Theo dõi (0) 0 Trả lời -


Biết \(\frac{7}{2}{x^2} - 2xy - 4x - y + \frac{{13}}{2} = A{\left( {x - 2} \right)^2} + B{\left( {2x - y + 1} \right)^2}\), tìm A và B?
bởi oops nani
 16/08/2020
Theo dõi (0) 0 Trả lời
16/08/2020
Theo dõi (0) 0 Trả lời -


2x2+2y2+z2+2xy-2xz-2yz-2x-2y+z=0
tìm x,y,z
Theo dõi (1) 10 Trả lời -


Tìm giá trị lớn nhất của biểu thức: N=-2y^2 - 3y +5?
bởi Thanh Thủyy
 10/08/2020
10/08/2020
Câu 1: Tìm giá trị lớn nhất của biểu thức:
N=-2y2 - 3y +5
P=(2-x).(x+4)
Câu 2: Cho a+b+c=0. Chứng minh a3 + b3 + c3 = 3abc
Theo dõi (1) 0 Trả lời -


Rút gọn biểu thức \(A=(x-1).(3-2x)-(5-2x).(5 +2x)\)?
bởi Nguyễn Nha
 09/08/2020
Theo dõi (1) 3 Trả lời
09/08/2020
Theo dõi (1) 3 Trả lời -


Tìm x, y, biết \(x^2 + y^2 - 2x + 2y + 2 = 0\)?
bởi Boy
 08/08/2020
Theo dõi (1) 1 Trả lời
08/08/2020
Theo dõi (1) 1 Trả lời -


Tìm giá trị nhỏ nhất của
a) A = 2x^2 + 4x + 2xy + y^2 + 7
b) B = 17 - 2/x^2-4x+5
c) C = x^2+10x+24/x^2+10x+26
Theo dõi (1) 2 Trả lời -


Phân tích ( 2x - 5/2)²
bởi Tống Phạm Thùy Dương
 29/07/2020
Bình Phương 1 hiệuTheo dõi (1) 3 Trả lời
29/07/2020
Bình Phương 1 hiệuTheo dõi (1) 3 Trả lời -


Biết \(0 \le x \le 1\) Tìm GTLN của \(A=x^2(1-x^3)\)?
bởi Bùi Cẩm Ly
 23/07/2020
23/07/2020
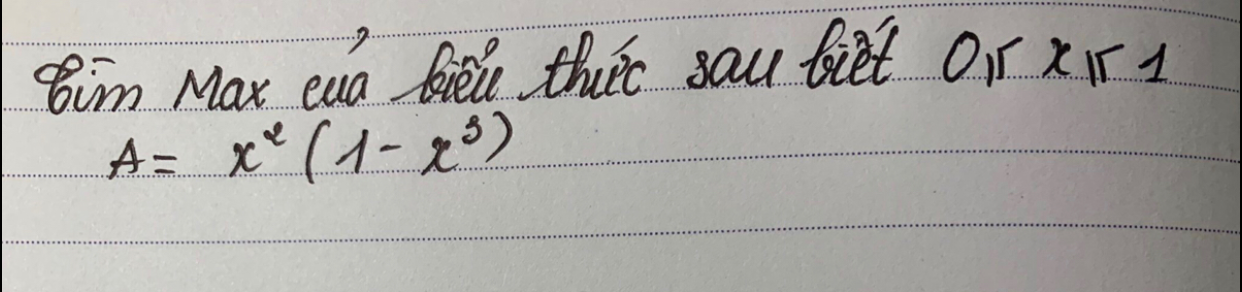 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Mọi người giải giúp mình vs ạTheo dõi (0) 1 Trả lời
Mọi người giải giúp mình vs ạTheo dõi (0) 1 Trả lời -

 Giá trị nhỏ nhất của biểu thứcA=9x^2-6x 4 đạt được khi x bằngTheo dõi (0) 4 Trả lời
Giá trị nhỏ nhất của biểu thứcA=9x^2-6x 4 đạt được khi x bằngTheo dõi (0) 4 Trả lời -


Tìm x biết (x +3)²– (x–4)(x +8)=1
bởi Nam--Master
 16/07/2020
(x 3)²– (x–4)(x 8)=1Theo dõi (0) 0 Trả lời
16/07/2020
(x 3)²– (x–4)(x 8)=1Theo dõi (0) 0 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình (x-1)/(x+2)-x/(x-2)=(5x-2)/(4-x^2)
bởi Thư Bùi
 26/04/2020
26/04/2020
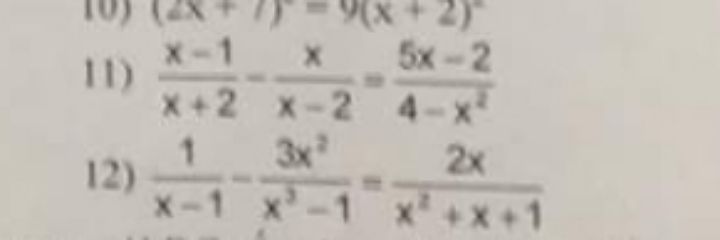 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm x biết x^2+2x+1 = 4(x^3 - 2x+1)
bởi Army
 17/04/2020
17/04/2020
Tìm x biết x^2+2x+1 = 4(x^3 - 2x+1)
Theo dõi (0) 0 Trả lời -


Giải phương trình x-3/x +1=x^2/x^2-1
bởi toan Nguyen
 04/04/2020
Hướng dẫn giải hai bài tập này với . Thanks các bạn
04/04/2020
Hướng dẫn giải hai bài tập này với . Thanks các bạn Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Khai triển (3x+4y)^2
bởi Thu Trang
 31/03/2020
31/03/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tính nhẩm 37^2+2.37+13^2
bởi Hieu Ha Van
 25/03/2020
Ai giải hộ mình bài này với nhaMinh đang cần gấp
25/03/2020
Ai giải hộ mình bài này với nhaMinh đang cần gấp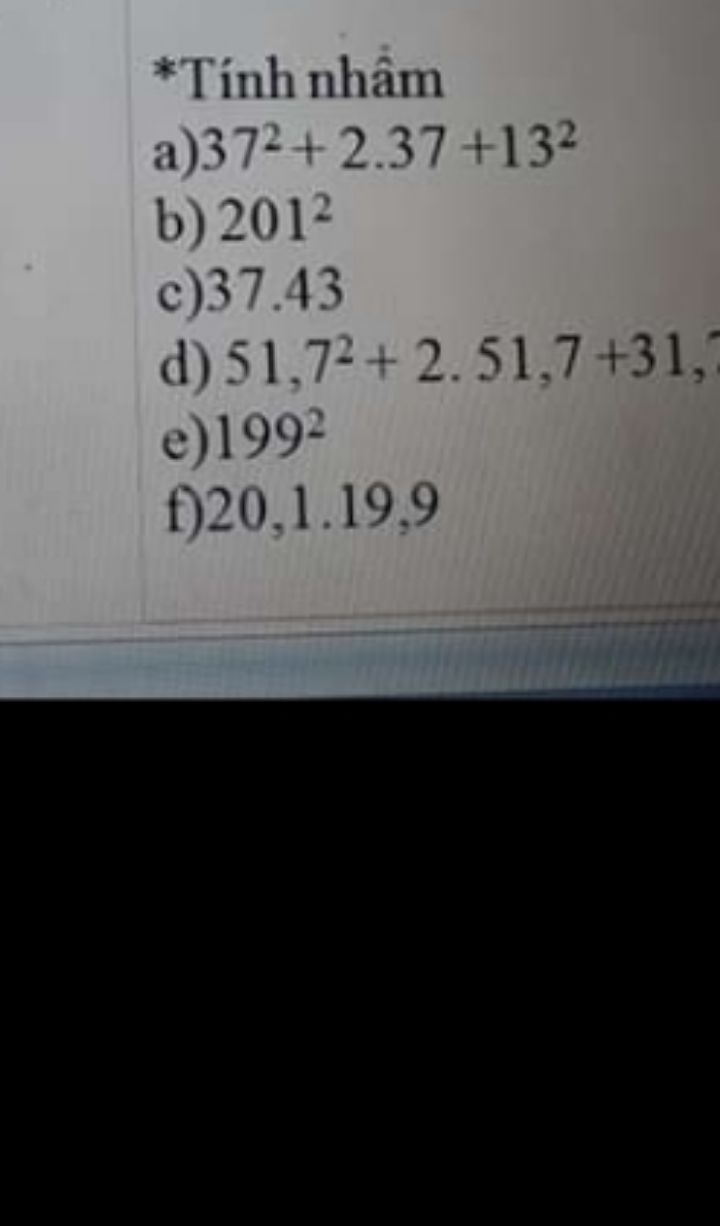 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Thực hiện phép tính (-2x^2)(x^3-3x^2-x+1)
bởi Minamoto Rinko
 27/02/2020
27/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Rút gọn biểu thức (2x+1)^2 +(2x+3)^2 -2(2x+a)(2x+3)
bởi Bông Thảo
 25/02/2020
25/02/2020
a, (2x+1)^2 +(2x+3)^2 -2(2x+a)(2x+3)
b, (2x-3)(2x+3)-(x+5)^2-(x-1)(x+2)
c, (24x^2 y^3 z^2-12x^3 y^2 z^3+36x^2 y^2 z^2): (-6x^2 y^2 z^2)
d, (x+2y)(x^2-2xy+4y^2)-(x-y)(x^2+xy+Y^2)
Theo dõi (0) 1 Trả lời -

 em không biết làmTheo dõi (0) 1 Trả lời
em không biết làmTheo dõi (0) 1 Trả lời -


Thực hiện phép tính (x+4)×(x^2-4x+16)
bởi Ha Mui
 29/01/2020
Thực hiện phép tínhTheo dõi (1) 5 Trả lời
29/01/2020
Thực hiện phép tínhTheo dõi (1) 5 Trả lời -


Thực hiện phép tính(2x+ 3y)^2
bởi Ha Mui
 29/01/2020
Thực hiện phép tínhTheo dõi (0) 4 Trả lời
29/01/2020
Thực hiện phép tínhTheo dõi (0) 4 Trả lời -


Thực hiện phép tính (2x+3y)^2
bởi Ha Mui
 29/01/2020
Thực hiện phép tínhTheo dõi (0) 4 Trả lời
29/01/2020
Thực hiện phép tínhTheo dõi (0) 4 Trả lời -


Tìm x biết 3x +2(5-x)=0
bởi Nguyen Văn Thành
 19/01/2020
19/01/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Cho các số thực x, y thoả mãn x² y² 5x = 2xy 2. Tìm giá trị lớn nhất của biểu thức B = 3x |+2y.
bởi Tatoo Thảo
 05/01/2020
Giúp mk vs ạ Mk cần gấpTheo dõi (0) 0 Trả lời
05/01/2020
Giúp mk vs ạ Mk cần gấpTheo dõi (0) 0 Trả lời -


Tính GTBT Q=x^2+a^2+y^2/b^2+z^2/c^2
bởi Lương Thùy Linh
 29/12/2019
29/12/2019
Cho a,b,c,x,y,z là các số thực thỏa mãn
và
. Tính giá trị của biểu thức Q=
.
Theo dõi (0) 1 Trả lời -


Thực hiện các phép tính (x+2)(x^2-2x+4)-(x^3+2)
bởi Nhỏ Bé
 21/12/2019
(x 2)(x^2-2x 4)-(x^3 2)
21/12/2019
(x 2)(x^2-2x 4)-(x^3 2)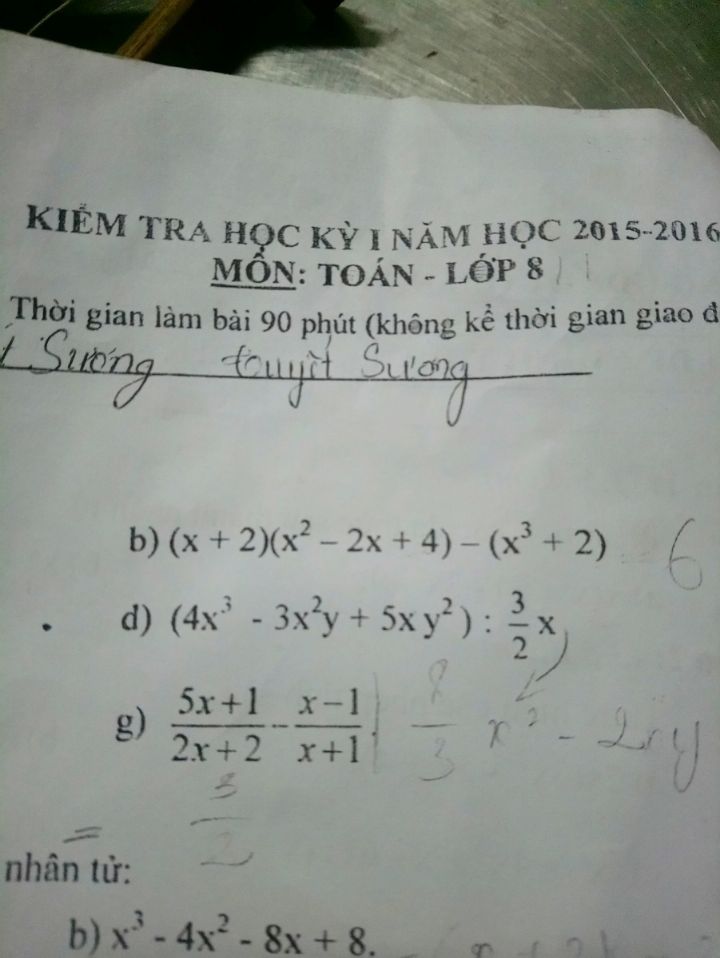 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Tìm x biết (3x-1).(x 5)=0
bởi Hợp Nguyễn
 30/09/2019
Tìm x biếtTheo dõi (1) 30 Trả lời
30/09/2019
Tìm x biếtTheo dõi (1) 30 Trả lời -


Tìm x biết (x+2).(x+3)-(x-2).(x+5)=0
bởi Nguyễn Nhật Linh
 12/08/2019
12/08/2019
1, tìm x :
a) (x+2).(x+3)-(x-2).(x+5)=0
b) (2x+3).(x-4)+(x-5).(x-2)=(x-4).(3x-5)
c) (3x-5).(7-5x)-(5x+2).(2-3x)=3
d)(x-7).(x+7)-(x-4)2-x=10+3
e) (x+1/2)2-(x-1).(x+1)=2x-1
2, Thu gọn :
a) (x+5)2-(3-x)2-2(x-4).(x+4)
b)4(x-1)2+(2x+3)2-8(x-2)(x+2)
Theo dõi (1) 18 Trả lời -


Rút gọn biểu thức A=(5x 5)^2 10(x-3)(1 x) x^2-6x 9C=(x-y-z)^2 2(x-y-z)(y z) (y z)^2
bởi Đỗ Mai
 11/08/2019
A=(5x 5)^2 10(x-3)(1 x) x^2-6x 9C=(x-y-z)^2 2(x-y-z)(y z) (y z)^2 Mn giúp mình với!!Theo dõi (0) 2 Trả lời
11/08/2019
A=(5x 5)^2 10(x-3)(1 x) x^2-6x 9C=(x-y-z)^2 2(x-y-z)(y z) (y z)^2 Mn giúp mình với!!Theo dõi (0) 2 Trả lời -


Tính nhanh 51,7-2x51,7x31,7+31,7^2
bởi Lại Lâm Nhi
 03/08/2019
03/08/2019
Tính nhanh:
51,7-2x51,7x31,7+31,72
Theo dõi (1) 9 Trả lời -


Tính 5(x+4)^2+4(x-5)^2-9(4+x)(4-x)
bởi Lưu Quang Ngọc
 27/06/2019
27/06/2019
a, 5(x+4)^2+4(x-5)^2-9(4+x)(4-x)
b, (x+2y)^2+(2x-y)^2+5(x+y)(x-y)-10(y-3)(y+3)
Moi nguoi giup mik nhe
Cam on rat nhieu
Theo dõi (0) 2 Trả lời -


Chứng minh a=b=c biết (a+b+c)^2 =3. (ab + ac + bc)
bởi ice 1509
 21/06/2019
21/06/2019
cho biết :
( a+b+c )2 = 3. ( ab + ac + bc )
chứng minh rằng a = b = c
Theo dõi (1) 12 Trả lời -


Tìm x, y biết x^2+2x-4y+y^2+5=0
bởi ice 1509
 21/06/2019
21/06/2019
a) x2 + 2x - 4y + y2 + 5= 0
b) 2x2 - 2xy + y2 - 4x +4= 0
Theo dõi (1) 7 Trả lời -


Chứng minh a^2+ab+b^2>=0 với mọi a, b
bởi Lương Thùy Linh
 08/04/2019
08/04/2019
Chứng minh rằng:
với mọi a,b
Giúp mk nhanh nha!MK đag cần gấp!
Theo dõi (0) 2 Trả lời -


Chứng minh (a+b)^2 = (a-b)^2+4ab
bởi Huỳnh Đức Minh Tiến
 09/09/2018
09/09/2018
CMR
(a+b)2 = (a-b)2+4ab
(a-b)2 = (a+b)2-4ab
Tính (a-b)2, biết a+b=7 và a.b=12
Tính (a+b)2, biết a-b=20 và a.b=3
Theo dõi (0) 4 Trả lời -


Tìm GTNN của biểu thức x^2-x+2018
bởi thuy tien
 21/09/2018
21/09/2018
giải giúp em bài này với tim giá trị nhỏ nhất của biểu thức x mũ 2-x+2018
Theo dõi (0) 1 Trả lời -


Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:
\(C=4u^4v^8+\left(u^2v^4\right)^4+4\)
Theo dõi (0) 2 Trả lời -


Tìm số nguyên x, y biết 4x^2+4y^2-4x-4=32
bởi Thanh Nguyên
 21/09/2018
21/09/2018
Tìm x,y biết \(4x^2+4y^2-4x-4=32\)
\(x,y\in Z\)
Ai nhanh tick cho ạ !!! I đang gấp !!!
Thanku !!
Theo dõi (0) 1 Trả lời -


Tìm GTNN của C=9x^2+y^2-2xy-8x+10
bởi Phạm Hoàng Thị Trà Giang
 21/09/2018
21/09/2018
C=9x\(^2\) +y\(^2\) -2xy -8x+10
Tìm Giá trị nhỏ nhất của biểu thức
Theo dõi (0) 2 Trả lời -


điền vào dấu ? để có hăng đẳng thức đúng
a/(?+?)^2=?+m+1/4
b/?-16y^4=(x+?)(x-?)
c/25a^2-?=(?+1/2b)(?-1/2b)
Theo dõi (0) 2 Trả lời -


Tìm x biết (x^2+2x-1)^2-9=0
bởi Trần Phương Khanh
 21/09/2018
21/09/2018
Gi ải phương trình:
(x2 + 2x - 1)2 - 9 = 0
Phân tích thành nhân tử: x2 + 2x - 4
Theo dõi (0) 1 Trả lời -


Chứng minh x^2-6x+10>0 với mọi x
bởi Goc pho
 21/09/2018
21/09/2018
1. CM:
a) x2 - 6x + 10 > 0 với mọi x
b) x2 - 4x + 7 > hoặc = 3 với mọi x
c) x2 + x + 1 > 0 với mọi x
d) x2 + y2 + 4x - 6y + 15 = 0 với mọi x
2. CM: (a - b)2 = (a + b)2 - 4ab
3. Cho x + y = 7 và xy = -3. Tính: x2 + y2
Theo dõi (0) 1 Trả lời -


Chứng minh (a+1)(b+1)(c+1) > =8 biết abc=1
bởi thu phương
 21/09/2018
21/09/2018
cho các số dưng thỏa abc=1.cm (a+1)(b+1)(c+1)\(\ge\)8
Theo dõi (0) 1 Trả lời -


\(50^2-49^2+48^2-47^2+...+2^2-1^2\)
Theo dõi (0) 1 Trả lời -


Tìm GTNN của x^2+6x+5
bởi An Nhiên
 06/09/2018
06/09/2018
Tìm min:
A= x2+6x+5
B= (x-1).(x-3)
C= x2-x+8
D= x2-3x
Theo dõi (0) 1 Trả lời -


A=(4+1)(4^2+1)(4^4+1)(4^8+1)(4^16+1)(4^32+1)
B=4^64-1
CMR:B=3A
Theo dõi (0) 1 Trả lời -


Chứng minh (a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca
bởi A La
 16/10/2018
16/10/2018
CMR:\(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
Theo dõi (0) 1 Trả lời -


Tìm GTLN của biểu thức -x^2+x+1/2
bởi hai trieu
 25/10/2018
25/10/2018
Đề bài: Tìm GTLN của biểu thức: ( theo hằng đẳng thức đáng nhớ )
5. -x mũ 2 + x + 1/2
6. -1/4x mũ 2 + x - 2
7. -1/9x mũ 2 - 1/3x + 1
8. -2x mũ 2 + 2xy - 2y mũ 2 + 2x + 2y - 8
Theo dõi (0) 3 Trả lời -


Tính (x-1/2)^2
bởi bach hao
 30/10/2018
30/10/2018
Tính (x-1/2)2
Theo dõi (0) 1 Trả lời -


Cho x + y=a và xy=b. Tính GTBT sau theo a và b:
a, x^2 + y^2
b, x^3 + y^3
c, x^4 + y^4
d, x^5 + y^5
Theo dõi (0) 1 Trả lời -


viết các biểu thức sau dưới dạng bình phương của một tổng hoặc hiệu
a/9a^2 -30a+25
b/1+4x+4x^2
c/a^2+16+8a
d/25x^2+4y^2-20xy
Theo dõi (0) 1 Trả lời -


Tìm GTNN của K = x^2+y^2+z^2 biết x + y + z = 1
bởi Lê Minh Trí
 28/03/2019
28/03/2019
Cho x + y + z = 1. Tìm GTNN của K = \(x^2+y^2+z^2\)
Theo dõi (0) 1 Trả lời -


Tìm x , biết :
( 5x - 1 ) ( x + 1 ) - 2 ( x - 3 )2 = ( x + 2 ) ( 3x - 1 ) - ( x + 4 )2 + ( x2 - x )
Các bạn giải nhanh cho mình câu này nha . Bạn nào giải chi tiết đúng mình tick cho.
Theo dõi (0) 1 Trả lời -


Tính A=(2+1) (2^2+1) (2^4+1) (2^8+1)
bởi Hy Vũ
 21/09/2018
21/09/2018
Tính A=(2+1) (22+1) (24+1) (28+1)
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức sau
A=\(^{2x^2+10y^2-6xy-6x-2y+16}\)
Help meee
Theo dõi (0) 2 Trả lời -


Tính tổng 2 lập phương 8x^3+6^4
bởi ngọc trang
 30/10/2018
30/10/2018
Giúp mk với nhanh nhanh nhé mai nộp rồi
Tính tổng hai lập phương hoặc hiệu hai lập phương
a, \(8x^3+6^4\)
b,\(125x^3+27y^3\)
c,\(27-y^3\)
d,\(125x-8y^3\)
e,\(125+x^3\)
g,\(x^3+216y^3\)
h,\(x^3-343y^3\)
i,\(125-27y^3\)
Theo dõi (0) 1 Trả lời -


Rút gọn 2x-(2x-1)^2-3x(x+3)(x-3)-4x(x+1)^2
bởi Suong dem
 21/09/2018
21/09/2018
Rút gọn:
2x-(2x-1)^2-3x(x+3)(x-3)-4x(x+1)^2
giải thích chi tiết giúp mình nha.Cần trong đêm nay.
Theo dõi (0) 1 Trả lời -


Tính M = ab + bc + ac biết ( a - b )^2 + ( b - c )^2 + ( a - c )^2 = a^2 + b^2 + c^2 và a + b + c = 6
bởi het roi
 30/10/2018
30/10/2018
Cho a, b, c là các số dướng thỏa mãn :
( a - b )2 + ( b - c ) 2 + ( a - c )2 = a2 + b2 + c2
và a + b + c = 6
Tính M = ab + bc + ac
Theo dõi (0) 1 Trả lời -


Tính (3x + 1)(3x - 1)
bởi Nguyễn Hạ Lan
 25/10/2018
25/10/2018
Tính :
1) ( 3x + 1 )( 3x - 1 )
2) ( 3x2 - y )( 3x2 + y )
3) ( 5x - 3/2 )( 5x + 3/2 )
4) ( x - 1 )( x2 + x + 1 )
5) ( x2 - 2 )( x4 + 2x2 + 4 )
6) ( x + 4 )( x2 - 4x + 16 )
7) ( 3x + 2 )( 9x2 - 6x + 4 )
8) ( x - 4 )( x2 + 4x + 16 )
9) ( x - 1/3 )( x2 + x/3 + 1/9 )
10) ( x + 1/3 )( x2 - 1/3x + 1/9 )
CÁC BẠN GIẢI NHANH CHO MÌNH NHA. BẠN NÀO GIẢI NHANH , ĐÚNG MÌNH TICK CHO
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A=(x+1)(2x-1)
bởi Lê Thánh Tông
 05/11/2018
05/11/2018
Tìm GTNN và GTLN
a)A=(x+1)(2x-1)
b)B=4x2-4xy+2y2+1|
c)C=5x-3x2+2
d)D=-8x2+4xy-y2+3
e)E=x2-8x+38
f)F=6x-x2+1Theo dõi (0) 1 Trả lời -


Tính ( x + y + z )^2
bởi Anh Trần
 25/10/2018
25/10/2018
Tính :
1) ( x + y + z )2
2) ( 1 - 5a )2
3) ( 5a - 4b )2
4) ( a - b - c )2
5) ( a + 1 )3
6) ( x + 2 )3
7) ( 2x + 3y )3
8) ( 4x + 2y )3
9) ( x - 3 )3
10) ( 4 - 4y2 )3
Các bạn giải nhanh cho mình nha. Bạn nào giải nhanh , đúng mình tick cho
Theo dõi (0) 1 Trả lời -


Chứng tỏ rằng 4x-x^2-5 < 0 với mọi x
bởi hi hi
 30/10/2018
30/10/2018
1:Chứng tỏ rằng:
\(4x-x^2-5\) <0 với mọi x
2:Tìm giá trị nhỏ nhất của các đa thức sau:
a)\(M=x^2+y^2-x+6y+10\)
b)\(Q=2x^2-6x\)
Theo dõi (0) 1 Trả lời -


Tìm x biết 27x^3+27x^2+9x+1=64
bởi Nguyễn Anh Hưng
 05/11/2018
05/11/2018
Tìm x
a)\(27x^3+27x^2+9x+1=64\) b)\(\left(x-2\right)^3-x^2\left(x-6\right)=4\) c)\(\left(x-1\right)^3-\left(x+3\right)\left(x^2-3x+9\right)+3\left(x-2\right)\left(x+2\right)=2\)Theo dõi (0) 1 Trả lời -


Tính (x + 4 ) (x^2 - 4x + 16)
bởi My Le
 30/10/2018
30/10/2018
Tính :
a) (x + 4 ) (x2 - 4x + 16)
b) (x - 3y ) ( x2 +3xy + 9y2)
TÍNH NGẮn GỌN GIÚP EM VS.
Theo dõi (0) 1 Trả lời -


Tìm GTLN của biểu thức A= 4x^2+2x
bởi Phan Thị Trinh
 05/11/2018
05/11/2018
Tìm GTLN
a, A= 4-\(x^2+2x\)
b , B=\(4x-x^2\)
Theo dõi (0) 2 Trả lời -


Tính A=3(x-1)^2-(x+1)^2+2.(x-3)(x+3)-(2x+3)^2-(5-20x)
bởi Bi do
 23/11/2018
23/11/2018
A=\(3\cdot\left(x-1\right)^2-\left(x+1\right)^2+2\cdot\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
Theo dõi (0) 2 Trả lời -


Viết tổng thành tích 9x^2 - 12xy + 4y^2 - 3
bởi Nguyễn Thanh Trà
 17/11/2018
17/11/2018
Viết tổng thành tích ( xoắn 3 đại số )
1. 9x mũ 2 - 12xy + 4y mũ 2 - 3
2. x mũ 2 + 4x + 1
3. x mũ 2 - 4x + 7
4. x mũ 2 + 6x + 15
5. x mũ 2 - x + 1/3
6. 1/4x mũ 2 + x
7. 3x mũ 2 + 2x + 1
8. 2x mũ 2 - 2x + 1
9. 10a mũ 2 + 5b mũ 2 + 12ab + 4a - 6b + 15
M.n giúp e ak, e sẽ tick cho mọi người, e đang cần gấp, e cảm ơn nhiều !!!!!!!!!!
Theo dõi (0) 1 Trả lời -


Viết tổng thành tích 9x^2 - 12xy + 4y^2 - 3
bởi thuy tien
 23/11/2018
23/11/2018
Viết tổng thành tích ( xoắn 3 đại số )
1. 9x mũ 2 - 12xy + 4y mũ 2 - 3
2. x mũ 2 + 4x + 1
3. x mũ 2 - 4x + 7
4. x mũ 2 + 6x + 15
5. x mũ 2 - x + 1/3
6. 1/4x mũ 2 + x
7. 3x mũ 2 + 2x + 1
8. 2x mũ 2 - 2x + 1
9. 10a mũ 2 + 5b mũ 2 + 12ab + 4a - 6b + 15
M.n giúp e ak, e sẽ tick cho mọi người, e cảm ơn nhiều !!!!!!!!!!
Theo dõi (0) 1 Trả lời -


Chứng minh a^2 chia 5 dư 1 biết a chia 5 dư 4
bởi trang lan
 25/10/2018
25/10/2018
Biết số tự nhiên a chia 5 dư 4.Chứng minh rằng \(a^2\) chia 5 dư 1
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức 2(x-y)(x+y)+(x+y)^2+(x-y)^2
bởi Thanh Truc
 30/10/2018
30/10/2018
Rút gọn biểu thức:
\(2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
Theo dõi (0) 1 Trả lời -


Chứng minh n^2 chia cho 3 thì dư 1 với n là một số tự nhiên không chia hết cho 3
bởi Suong dem
 05/11/2018
05/11/2018
cho n là một số tự nhiên không chia hết cho 3. khẳng định n2 chia cho 3 thì dư 1
Theo dõi (0) 1 Trả lời -


Tính nhanh A=2018^2-2017^2
bởi Hoa Lan
 30/10/2018
30/10/2018
Tính nhanh :
a ) A=\(2018^2-2017^2\)
b ) \(B=2018^2-2017^2+2016^2-2015^2+...+2^2-1^2\)
Theo dõi (0) 1 Trả lời -


Tìm x biết 16x^2-(4x-5)^2=15
bởi Nguyễn Thanh Trà
 30/10/2018
30/10/2018
Tìm x :
a ) \(16x^2-\left(4x-5\right)^2=15\)
b ) \(\left(2x+3\right)^2\)\(-4.\left(x-1\right).\left(x+1\right)=49\)
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức R=x^2+2y^2+2xy-2y
bởi Bo bo
 30/10/2018
30/10/2018
tìm giá trị nhỏ nhất R=x2+2y2+2xy-2y
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức Q=3/2x^2+x+1
bởi Nguyễn Trà Giang
 05/11/2018
05/11/2018
tìm giá trị nhỏ nhất
Q=\(\dfrac{3}{2}\)x2+x+1
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức (2x-3)^2-(4x-6)(2x-5)+(2x-5)^2
bởi Goc pho
 05/11/2018
05/11/2018
Rút gọn biểu thức :\(\left(2x-3\right)^2-\left(4x-6\right)\left(2x-5\right)+\left(2x-5\right)^2\)
Theo dõi (0) 1 Trả lời -


So sánh (a-b)^2 và (b-a)^2
bởi Suong dem
 25/10/2018
25/10/2018
so sánh
(a-b)^2 và (b-a)^2
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức x^2+3x+3
bởi Hy Vũ
 25/10/2018
25/10/2018
tìm giá trị nhỏ nhất x2+3x+3
Theo dõi (0) 1 Trả lời -


( x ^2 - 1 ) ^3 - ( x ^4 + x ^2 +1 ) . ( x ^2 - 1 ) = 0
Theo dõi (0) 1 Trả lời -


Chứng minh 2(x^3+y^3)-3(x^2+y^2) không phụ thuộc vào biến
bởi Quế Anh
 25/10/2018
25/10/2018
I : C/m các biểu thức sau không phụ thuộc vào biến
a) 2(x^3+y^3)-3(x^2+y^2) với x+y=1
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức(2x-1)(4x^2+2x+1)-8x^3+16x
bởi Lan Anh
 30/10/2018
30/10/2018
Rút gọn biểu thức:
a)(2x-1)(4x^2+2x+1)-8x^3+16x
b)(x+2)^3-x^2(x+6)-2x-5
Theo dõi (0) 1 Trả lời -


Tìm GTLN của biểu thức A=-x^2-4x-2
bởi thu phương
 25/10/2018
25/10/2018
bài 1 tìm gtnn của biểu thức sau
G=(3x^2+y-2xy-7)
bài 2 tìm gtln của các biểu thức sau
A=-x^2-4x-2
B=-2x^2-3x+5
mn ơi giúp mình với ạ mình đang cần gấp ạTheo dõi (0) 1 Trả lời -


Tính a^4+b^4+c^4 biết a+b+c=0, a^2+b^2+c^2=1
bởi Chai Chai
 25/10/2018
25/10/2018
Cho a+b+c=0
a2+b2+c2=1
Tính a4+b4+c4
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức M= x^2+y^2-x+6y+10
bởi Tram Anh
 25/10/2018
25/10/2018
Tìm giá trị nhỏ nhất của đa thức sau:
M= x2+y2-x+6y+10
(Trình bày từng bước nhé!)
Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức P=x^3+y^3+3xy biết x+y=1
bởi can chu
 05/11/2018
05/11/2018
Cho x+y=1. Tính giá trị của:
a) \(P=x^3+y^3+3xy\)
b) \(Q=x^3+y^3+3xy\left(x^2+y^2\right)+6x^2y^2\left(x+y\right)\)
Theo dõi (0) 1 Trả lời -


( 3+1) . ( 32 +1) . ( 34 +1) . ( 36+ 1) . ( 38+ 1 ) . (316 + 1)
Theo dõi (0) 1 Trả lời -


Tìm x biết (x+4)^2-(x+1)(x-1)=16
bởi thu hảo
 30/10/2018
30/10/2018
Tìm x , biết :
\(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=16\)
Theo dõi (0) 1 Trả lời -


Tìm x biết (3x-5)(5-3x)+9(x+1)^2=30
bởi thủy tiên
 05/11/2018
05/11/2018
Tìm x , biết :
\(\left(3x-5\right)\left(5-3x\right)+9\left(x+1\right)^2=30\)
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức :
\(\left(m^3-m+1\right)^2+\left(m^2-3\right)^2-2\left(m^2-3\right)\left(m^3-m+1\right)\)
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức Q=(a+b+1)^3-(a+b-1)^3-6(a+b)^2
bởi Lê Minh
 25/10/2018
25/10/2018
rút gọn biểu thức:
Q=(a+b+1)3-(a+b-1)3-6(a+b)2
Theo dõi (0) 1 Trả lời -


Rút gọn 9x^2-16y+5-6x+16y^2
bởi Phan Thị Trinh
 25/10/2018
25/10/2018
Rút gọn:
9x^2-16y+5-6x+16y^2
Theo dõi (0) 1 Trả lời





