Bài tập 4 trang 8 SGK Giải tích 12 nâng cao

Tập xác định \(D=\mathbb{R}\)

y' = a - 3x²

- Nếu a < 0 thì y' < 0 với mọi x \(\in\) \(\mathbb{R}\), khi đó hàm số nghịch biến trên \(\mathbb{R}\).

- Nếu a = 0 thì \(y'=-3x^2\leq 0\) với mọi x \(\in\) \(\mathbb{R}\), đẳng thức chỉ xảy ra với x = 0. Vậy hàm số nghịch biến trên \(\mathbb{R}\).

- Nếu a > 0 thì \(y'=0\Leftrightarrow x=\pm \sqrt{\frac{a}{3}}\)

Ta có bảng biến thiên

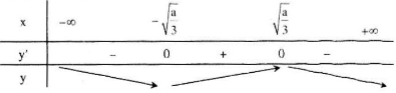
Trong trường hợp này: Hàm số không đồng biến trên \(\mathbb{R}\).

Vậy hàm số nghịch biến trên \(\mathbb{R}\) khi và chỉ khi \(a\leq 0\).

-- Mod Toán 12 HỌC247