Giải bài 10 tr 9 sách GK Toán GT lớp 12 Nâng cao
Số dân của một thị trấn sau t năm kể từ năm 1970 ước tính bởi công thức \(f(t)=\frac{26t+10}{t+5}\)(f(x) được tính bằng nghìn người)
a) Tính số dân của thị trấn vào đầu năm 1980 và đầu năm 1995
b) Xem f là một hàm số xác định trên nữa khoảng \([0; +\infty )\). Tính f'(t) và xét chiều biến thiên của f trên nữa khoảng \([0; +\infty )\).
c) Đạo hàm của hàm số f biểu thị tốc độ tăng dần số cảu thị trấn (tính bằng nghìn người/ năm)
- Tính tốc độ tăng dân số vào đầu năm 1990 của thị trấn
- Tính tốc độ tăng dân số được dự kiến vào năm 2008.
- Vào năm nào thì tốc độ tăng dân số là 0,125 nghìn người/ năm.
Hướng dẫn giải chi tiết
Câu a:
Vào đầu năm 1980, ta có t = 10; f(10) = 18
Vậy số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
Vào đầu năm 1995, ta có t = 25; f(25) = 22
Số dân của thị trấn vào đầu năm 1995 là 22 nghìn người.
Câu b:
\(f'(t)=\frac{120}{(t+5)^2}\) với mọi t > 0; f(t) liên tục trên \([0; +\infty )\) (vì liên tục trên khoảng \((-5;+\infty )\)
Vậy hàm số đồng biến trên \([0; +\infty )\)
Câu c:
Tốc độ tăng dần số vào đầu năm 1990 là:
\(f'(20)=\frac{120}{25^2}=0,192\) (do t = 1990 - 1970 = 20)
Tốc độ tăng dân số được dự kiến vào năm 2008 của thị trấn là:
\(f'(38)=\frac{120}{43^2}\approx 0,065\) (do t = 2008 - 1970 = 38)
Ta có f'(t) = 0,125
\(\Leftrightarrow \frac{120}{(t+5)^2}=0,125\Leftrightarrow t+5= \sqrt{\frac{120}{0,125}}\approx 31\Rightarrow t \approx 26\)
Vậy vào năm 1996. Tốc độ tăng dân số của thị trấn là 0,125.
-- Mod Toán 12 HỌC247
-


Xét tính đồng biến, nghịch biến của hàm số
bởi phan vy
 14/05/2021
14/05/2021
Xét tính đồng biến, nghịch biến:
a) y=b) y=
c) y=
c) y=
Theo dõi (0) 6 Trả lời -


Cho hàm số f(x). Hàm số f'(x) có đồ thị như hình bên
bởi Thảo Còi'ss
 08/05/2021
Giúp e với ạ
08/05/2021
Giúp e với ạ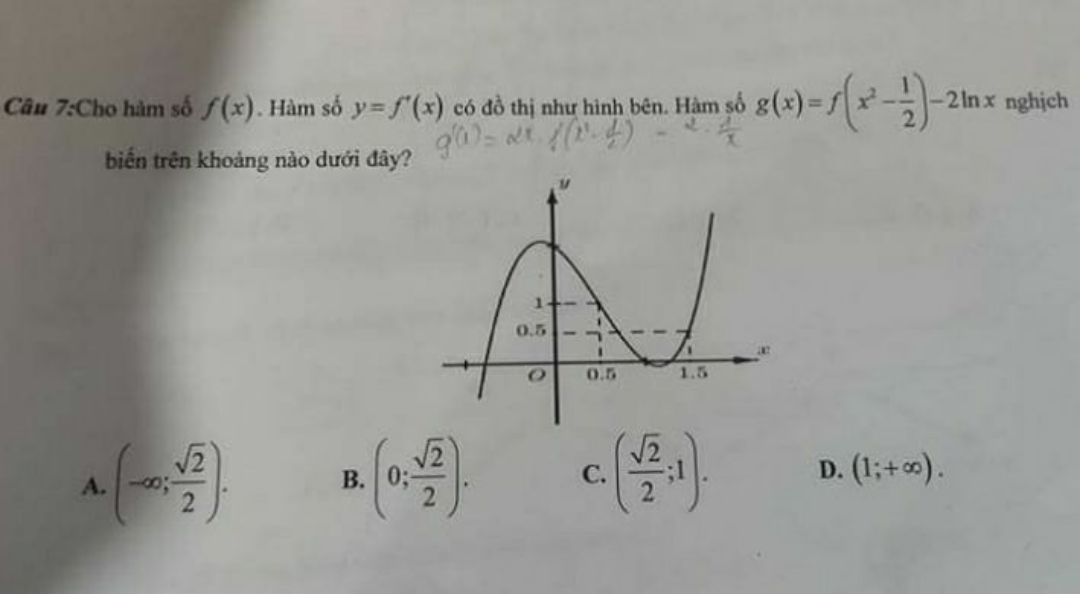 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh bất đẳng thức sau: \(\tan x>x+\dfrac{{{x}^{3}}}{3}\) \(( 0 < x < \frac{\pi }{2} ) \).
bởi Nguyễn Trà Giang
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Chứng minh bất đẳng thức sau: \(\tan x>x\) ( \(0 < x < \frac{\pi }{2})\)
bởi Nguyễn Trọng Nhân
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Chứng minh rằng hàm số \(y=\sqrt{2x-{{x}^{2}}}\) đồng biến trên khoảng \(\left( 0;\ 1 \right)\) và nghịch biến trên khoảng \(\left( 1;\ 2 \right).\)
bởi Trần Phương Khanh
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Chứng minh rằng hàm số \(y=\dfrac{x}{{{x}^{2}}+1}\) đồng biến trên khoảng \(\left( -1;\ 1 \right)\) và nghịch biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 1;+\infty \right).\)
bởi Thùy Trang
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Xét sự đồng biến, nghịch biến của hàm số: \(y = x^4\) - \(2x^2\) +\( 3\)
bởi Trần Hoàng Mai
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Xét sự đồng biến, nghịch biến của hàm số: \(y ={1 \over 3}x^3\) + \(3x^2-7x - 2\)
bởi Mai Đào
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 8 trang 8 SGK Giải tích 12 Nâng cao
Bài tập 9 trang 9 SGK Giải tích 12 Nâng cao
Bài tập 1.1 trang 7 SBT Toán 12
Bài tập 1.2 trang 7 SBT Toán 12
Bài tập 1.3 trang 8 SBT Toán 12
Bài tập 1.4 trang 8 SBT Toán 12
Bài tập 1.5 trang 8 SBT Toán 12
Bài tập 1.6 trang 8 SBT Toán 12
Bài tập 1.7 trang 8 SBT Toán 12
Bài tập 1.8 trang 8 SBT Toán 12
Bài tập 1.9 trang 8 SBT Toán 12
Bài tập 1.10 trang 8 SBT Toán 12
Bài tập 1.11 trang 9 SBT Toán 12
Bài tập 1.12 trang 9 SBT Toán 12
Bài tập 1.13 trang 9 SBT Toán 12
Bài tập 1.14 trang 9 SBT Toán 12
Bài tập 1.15 trang 9 SBT Toán 12
Bài tập 1.16 trang 9 SBT Toán 12
Bài tập 1 trang 7 SGK Toán 12 NC
Bài tập 2 trang 7 SGK Toán 12 NC
Bài tập 3 trang 8 SGK Toán 12 NC
Bài tập 4 trang 8 SGK Toán 12 NC
Bài tập 5 trang 8 SGK Toán 12 NC
Bài tập 6 trang 8 SGK Toán 12 NC
Bài tập 7 trang 8 SGK Toán 12 NC
Bài tập 8 trang 8 SGK Toán 12 NC







