Giải bài 1.2 tr 7 SBT Toán 12
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a) \({y = \frac{{3 - 2x}}{{x + 7}}}\);
b) \(y = \frac{1}{{{{(x - 5)}^2}}}\);
c) \(y = \frac{{2x}}{{{x^2} - 9}}\);
d) \(y = \frac{{{x^4} + 48}}{x}\);
e) \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\);
g) \(y = \frac{{{x^2} - 5x + 3}}{{x - 2}}\).
Hướng dẫn giải chi tiết
a) TXĐ: \ {-7}.
\(y' = \frac{{ - 17}}{{{{(x + 7)}^2}}}\)
trên các khoảng nên hàm số nghịch biến trên các khoảng đó.
b) TXĐ: \ {5}
\(y' = \frac{{ - 2}}{{{{(x - 5)}^3}}}\)
trên khoảng nên y nghịch biến trên khoảng .
trên khoảng nên y đồng biến trên khoảng .
c) TXĐ: \{-3;3}
\(y' = \frac{{ - 2({x^2} + 9)}}{{{{({x^2} - 9)}^2}}}\)
trên các khoảng nên hàm số nghịch biến trên các khoảng đó.
d) TXĐ: \{0}
\(\begin{array}{l}
y' = \frac{{3\left( {{x^4} - 16} \right)}}{{{x^2}}} = \frac{{3\left( {{x^2} - 4} \right)\left( {{x^2} + 4} \right)}}{{{x^2}}}\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 2\\
x = 2
\end{array} \right.
\end{array}\)
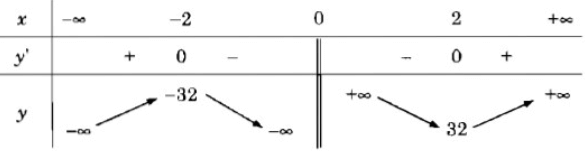
Bảng biến thiên:
Vậy hàm số đã cho đồng biến trên các khoảng và nghịch biến trên các khoảng
e) TXĐ: \{-1}
\(\begin{array}{l}
y' = \frac{{{x^2} + 2x - 5}}{{{{\left( {x + 1} \right)}^2}}}\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 1 - \sqrt 6 \\
x = - 1 + \sqrt 6
\end{array} \right.
\end{array}\)
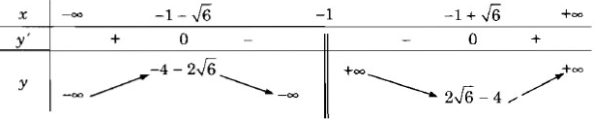
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng \(( - \infty ; - 1 - \sqrt 6 ),( - 1 + \sqrt 6 ; + \infty )\)
và nghịch biến trên các khoảng \(( - 1 - \sqrt 6 ; - 1),( - 1; - 1 + \sqrt 6 )\)
g) TXĐ: \{2}
\(y' = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\) (do \({x^2} - 4x + 7\) có \(\Delta ' = - 3 < 0\))
Vậy hàm số đã cho đồng biến trên các khoảng
-- Mod Toán 12 HỌC247
-


Cho đồ thị hàm số y = -x3 như hình vẽ. Hàm số \(y = - {x^3}\) nghịch biến trên khoảng:
bởi Nguyễn Thủy
 26/01/2021
26/01/2021
.png)
A. (-1;0) B. (-∞;0)
C. (0;+∞) D. (-1;1)
Theo dõi (0) 2 Trả lời -


.png)
Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- π/2 ; 3π/2]
Theo dõi (0) 1 Trả lời -


Có bao nhiêu giá trị nguyên của tham số m, để hàm số đã cho đồng biến trên từng khoảng xác định của nó?
bởi Tiên Thủy
 15/09/2020
E cần gấp ạ
15/09/2020
E cần gấp ạ Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Giải phương trình y=x^4+4x^2+5.
bởi nguyễn hữu Tiên
 14/09/2020
14/09/2020
y=x^4+4x^2+5
Theo dõi (1) 6 Trả lời -


Xét tính đơn điệu của hàm số, biết y= (3 - x)/x.
bởi Nguyễn Selina
 14/09/2020
14/09/2020
y= (3 - x)/x
y= x + 1/x
Theo dõi (2) 1 Trả lời -


Hàm số (2{x^4} + 1) đồng biến trên khoảng nào?
bởi Nguyên Uyên
 14/09/2020
Giúp mik vớiTheo dõi (0) 3 Trả lời
14/09/2020
Giúp mik vớiTheo dõi (0) 3 Trả lời -


Xét tính đơn điệu của hàm số y=x + 1/x
bởi Nguyễn Thị Tĩnh
 14/09/2020
14/09/2020
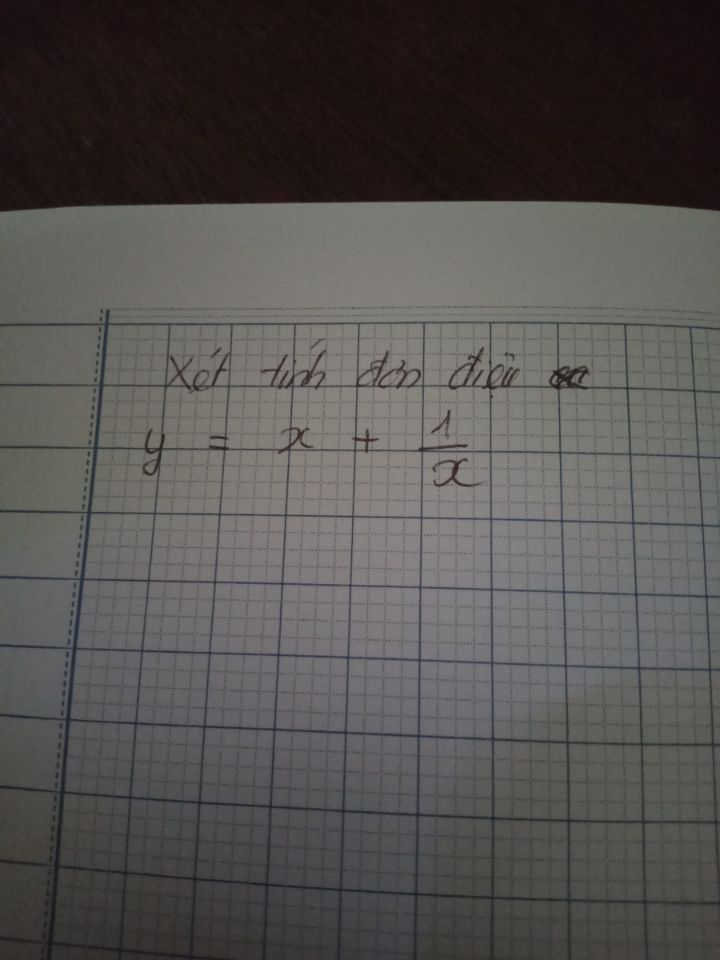 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Giải giúp e vs ạ
Giải giúp e vs ạ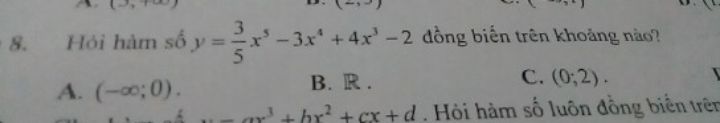 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Nếu hàm số y=f(x)liên tục và đồng biến trên khoảng ( -2;3) thì hàm số y=f(x) + 3 đồng biến trên khoảng nào?
bởi Tien Cao
 12/09/2020
12/09/2020
A. khoảng(1;6)
B. khoảng( 5;0)
C. khoảng( 2;6)
D. khoảng(- 2;3)
giúp em với ạ cả cách giải càng tốt ạTheo dõi (0) 6 Trả lời -


Xét tính đơn điệu của y= 3-2x
bởi Đỗ Hoài
 12/09/2020
Lập cả bảng biến thiênTheo dõi (0) 1 Trả lời
12/09/2020
Lập cả bảng biến thiênTheo dõi (0) 1 Trả lời -


Tìm khoảng đồng biến nghịch biến của hàm số y=x căn(4-x)
Theo dõi (0) 1 Trả lời -


Tìm tất cả gt m sao cho hàm số y tăng trên từng khoảng xđ của nó. Biết y=x^2-(m+1)+2m-1/x-m
bởi Thanh Ngân
 11/09/2020
11/09/2020
y=x^2-(m+1)+2m-1/x-m
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 10 trang 9 SGK Giải tích 12 Nâng cao
Bài tập 1.1 trang 7 SBT Toán 12
Bài tập 1.3 trang 8 SBT Toán 12
Bài tập 1.4 trang 8 SBT Toán 12
Bài tập 1.5 trang 8 SBT Toán 12
Bài tập 1.6 trang 8 SBT Toán 12
Bài tập 1.7 trang 8 SBT Toán 12
Bài tập 1.8 trang 8 SBT Toán 12
Bài tập 1.9 trang 8 SBT Toán 12
Bài tập 1.10 trang 8 SBT Toán 12
Bài tập 1.11 trang 9 SBT Toán 12
Bài tập 1.12 trang 9 SBT Toán 12
Bài tập 1.13 trang 9 SBT Toán 12
Bài tập 1.14 trang 9 SBT Toán 12
Bài tập 1.15 trang 9 SBT Toán 12
Bài tập 1.16 trang 9 SBT Toán 12
Bài tập 1 trang 7 SGK Toán 12 NC
Bài tập 2 trang 7 SGK Toán 12 NC
Bài tập 3 trang 8 SGK Toán 12 NC
Bài tập 4 trang 8 SGK Toán 12 NC
Bài tập 5 trang 8 SGK Toán 12 NC
Bài tập 6 trang 8 SGK Toán 12 NC
Bài tập 7 trang 8 SGK Toán 12 NC
Bài tập 8 trang 8 SGK Toán 12 NC