Giải bài 1.7 tr 8 SBT Toán 12
Chứng minh các bất đẳng thức sau:
a) \(\tan x > \sin x,0 < x < \frac{\pi }{2}\)
b) \(1 + \frac{1}{2}x - \frac{{{x^2}}}{8} < \sqrt {1 + x} < 1 + \frac{1}{2}\) với x > 0.
Hướng dẫn giải chi tiết
a) Xét hàm \(f\left( x \right) = \tan x - \sin x\) trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) ta có:
\(f'\left( x \right) = \frac{1}{{{{\cos }^2}x}} - \cos x\)\(=\frac{{1 - {{\cos }^3}x}}{{{{\cos }^2}x}} > 0\) với \(\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Vì \(\cos x < 1\) với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\)
Nên \({\cos ^3}x < 1,\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Do đó hàm số \(f\left( x \right) = \tan x - \sin x\) đồng biến trên \(\left( {0;\frac{\pi }{2}} \right)\)
\( \Rightarrow f\left( x \right) > f\left( 0 \right) = 0\)
\( \Rightarrow \tan x - \sin x > 0 \Leftrightarrow \tan x > \sin x\) với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\).
b) Xét \(f\left( x \right) = 1 + \frac{1}{2}x - \frac{{{x^2}}}{8} - \sqrt {1 + x} \) trên (0;+∞) ta có:
\(f'\left( x \right) = \frac{1}{2} - \frac{1}{4}x - \frac{1}{{2\sqrt {x + 1} }}\)
Vì x>0 nên \(f'\left( x \right) < \frac{1}{2} - \frac{1}{4}.0 - \frac{1}{{2\sqrt {0 + 1} }} = 0\)
Suy ra hàm số y = f(x) nghịch biến trên (0;+∞)
Do đó: \(f\left( x \right) < f\left( 0 \right) = 0 \)
\(\Rightarrow 1 + \frac{1}{2}x - \frac{{{x^2}}}{8} - \sqrt {1 + x} < 0\)
\(\Leftrightarrow 1 + \frac{1}{2}x - \frac{{{x^2}}}{8} < \sqrt {1 + x} \,\,\,\left( 1 \right)\)
Xét \(g\left( x \right) = \sqrt {1 + x} - 1 - \frac{1}{2}x\) trên (0;+∞) ta có: \(g'\left( x \right) = \frac{1}{{2\sqrt {x + 1} }} - \frac{1}{2}\)
Vì x>0 nên \(g'\left( x \right) < \frac{1}{{2\sqrt {0 + 1} }} - \frac{1}{2} = 0\) hay y = g(x) nghịch biến trên (0;+∞)
Do đó g(x)
Từ (1) và (2) ta được :
\(1 + \frac{1}{2}x - \frac{{{x^2}}}{8} < \sqrt {1 + x} < 1 + \frac{1}{2}x\) với x > 0. (đpcm)
-- Mod Toán 12 HỌC247
-


Tìm tập nghiệm của bất phương trình -1
bởi Minh Vương
 24/04/2020
Thầy cô giải giúp em với ạ
24/04/2020
Thầy cô giải giúp em với ạ Theo dõi (0) 10 Trả lời
Theo dõi (0) 10 Trả lời -


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tất cả các giá trị của tham số m sao cho hàm số y=(mx-9)/(x-m) đồng biến trên khoảng 2 đến dương vô cùng
bởi anhh
 20/04/2020
help
20/04/2020
help Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính đạo hàm của hàm số y = ( x^2+x+1)^1/3
bởi Lê Thanh Ánh
 16/04/2020
16/04/2020
Tính đạo hàm của hàm số y = ( x^2+x+1)^1/3
Theo dõi (1) 3 Trả lời -


Có bao nhiêu giá trị của m để hàm số nghịch biến?
bởi Hùng Quang
 11/04/2020
11/04/2020
Câu 29
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tại sao phải chứng minh Fx đồng biến
bởi Bắc Nguyễn
 07/04/2020
Tại sao Fx phải đồng biến ?Đồng biến để làm gì ?
07/04/2020
Tại sao Fx phải đồng biến ?Đồng biến để làm gì ? Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm giá trị thực của tham số m để hàm số y=2x^3-3(m+2)+x^2+6(m+1) x-3m+5 luôn đồng biến trên R
bởi Duong Ninh
 07/04/2020
07/04/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


TÌm tất cả các số nguyên n sao cho: 4n3+n+3 chia hết cho 2n2+n+1
Theo dõi (0) 2 Trả lời -


Hàm số y= -x^3+3x đồng biến trên khoảng nào?
bởi Hường Em
 01/04/2020
giải ra và đáp án
01/04/2020
giải ra và đáp án Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Có bao nhiêu số nguyên dương m để hàm số y=2/3x^3-(2m+9)x^2+2(m^2+9m)x+10 nghịch biến trên khoảng (3; 6)?
bởi sunshine
 29/03/2020
C31
29/03/2020
C31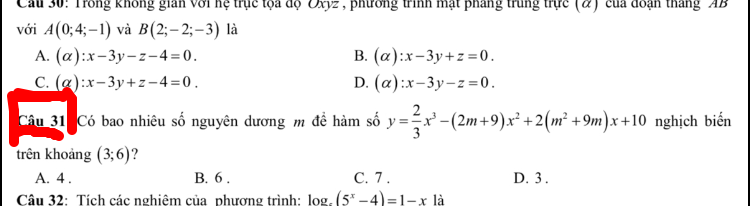 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


Hàm số y=x^3-3x+1 nghịch biến trên những khoảng nào?
bởi Lê Thị Huyền
 26/03/2020
26/03/2020
 Theo dõi (0) 16 Trả lời
Theo dõi (0) 16 Trả lời -


 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời
Bài tập SGK khác
Bài tập 1.5 trang 8 SBT Toán 12
Bài tập 1.6 trang 8 SBT Toán 12
Bài tập 1.8 trang 8 SBT Toán 12
Bài tập 1.9 trang 8 SBT Toán 12
Bài tập 1.10 trang 8 SBT Toán 12
Bài tập 1.11 trang 9 SBT Toán 12
Bài tập 1.12 trang 9 SBT Toán 12
Bài tập 1.13 trang 9 SBT Toán 12
Bài tập 1.14 trang 9 SBT Toán 12
Bài tập 1.15 trang 9 SBT Toán 12
Bài tập 1.16 trang 9 SBT Toán 12
Bài tập 1 trang 7 SGK Toán 12 NC
Bài tập 2 trang 7 SGK Toán 12 NC
Bài tập 3 trang 8 SGK Toán 12 NC
Bài tập 4 trang 8 SGK Toán 12 NC
Bài tập 5 trang 8 SGK Toán 12 NC
Bài tập 6 trang 8 SGK Toán 12 NC
Bài tập 7 trang 8 SGK Toán 12 NC
Bài tập 8 trang 8 SGK Toán 12 NC





