Giải bài 1.4 tr 8 SBT Toán 12
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \({y = x - \sin x,x \in [0;2\pi ]}\);
b) \({y = \sin \frac{1}{x},(x > 0)}\).
Hướng dẫn giải chi tiết
a) \({y = x - \sin x,x \in \left[ {0;2\pi } \right]}\)
\(y' = 1 - \cos x \ge 0\) với mọi \(x \in \left[ {0;2\pi } \right]\)
Dâu “=” xảy ra chỉ tại và \(x = 2\pi \).
Vậy hàm số đồng biến trên đoạn \(\left[ {0;2\pi } \right]\).
b) Xét hàm số \(y = \sin \frac{1}{x}\) với x > 0
\(y' = - \frac{1}{{{x^2}}}cos\frac{1}{x}\).
Giải bất phương trình sau trên khoảng :
\(\begin{array}{l}
\frac{1}{{{x^2}}}\left( { - \cos \frac{1}{x}} \right) > 0 \Leftrightarrow \cos \frac{1}{x} < 0\\
\Leftrightarrow \frac{\pi }{2}\left( {1 + 4k} \right) < \frac{1}{x} < \frac{\pi }{2}\left( {3 + 4k} \right),k = 0,1,2...\\
\Leftrightarrow \frac{2}{{\pi \left( {1 + 4k} \right)}} > x > \frac{2}{{\pi \left( {3 + 4k} \right)}},k = 0,1,2...
\end{array}\)
Do đó hàm số đồng biến trên các khoảng
\(...,\left( {\frac{2}{{\left( {4k + 3} \right)\pi }};\frac{2}{{\left( {4k + 1} \right)\pi }}} \right),\left( {\frac{2}{{\left( {4k - 1} \right)\pi }};\frac{2}{{\left( {4k - 3} \right)\pi }}} \right)\)
\(,...,\left( {\frac{2}{{7\pi }};\frac{2}{{5\pi }}} \right),\left( {\frac{2}{{3\pi }};\frac{2}{\pi }} \right)\)
và nghịch biến trên các khoảng
\(...,\left( {\frac{2}{{\left( {4k + 1} \right)\pi }};\frac{2}{{\left( {4k - 1} \right)\pi }}} \right),...,\left( {\frac{2}{{5\pi }};\frac{2}{{3\pi }}} \right)\)
\(,\left( {\frac{2}{\pi }; + \infty } \right)\) với k = 0, 1, 2,...
-- Mod Toán 12 HỌC247
-


Tính y trong bảng biến thiên đã cho.
bởi Nguyễn Phấn
 08/09/2020
08/09/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm m để hàm số y đồng biến (nghịch biến) trên R.
bởi Như Quỳnh
 08/09/2020
Giúp em với ạ.
08/09/2020
Giúp em với ạ.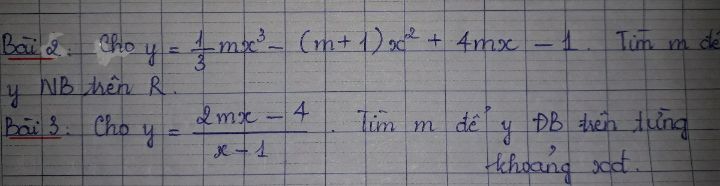 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Xét tính đồng biến , nghịch biến của hàm số
bởi Như Quỳnh
 08/09/2020
Giúp mình với!!!
08/09/2020
Giúp mình với!!! Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh rằng: sinx < x với mọi x thuộc (0; ∞)
bởi Như Quỳnh
 08/09/2020
Giúp mình với ạ.Chứng minh rằng: sinx < x với mọi x thuộc (0; ∞)Theo dõi (1) 0 Trả lời
08/09/2020
Giúp mình với ạ.Chứng minh rằng: sinx < x với mọi x thuộc (0; ∞)Theo dõi (1) 0 Trả lời -


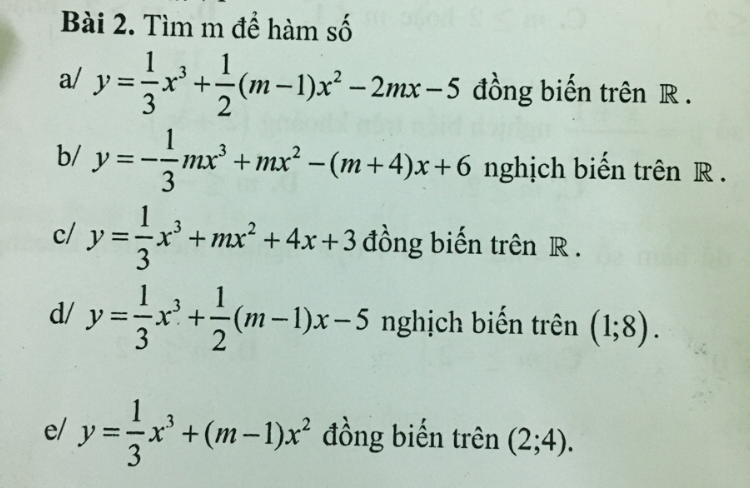 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tham số m để hàm số y = 1/3mx^3-(m-1)x^2 3(m-2)x 1/3 đồng biến trên [2; vô cực)
bởi Võ Nguyễn Yến Nhi
 06/09/2020
06/09/2020
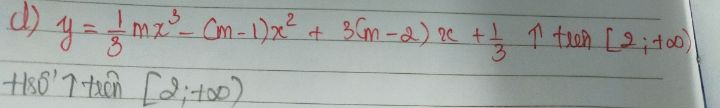 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho em xin lời giải ạ
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tìm m để hàm số \(y=\dfrac{1}{3}x^3+ (m +1)x^2-(m +1)x +1\) đồng biến?
bởi nguyễn thị hà chi
 13/08/2020
Theo dõi (0) 1 Trả lời
13/08/2020
Theo dõi (0) 1 Trả lời -


Tìm tính đơn điệu của hàm số \(y=\sqrt {2x^2+1}\)?
bởi Đặng Linh
 10/08/2020
10/08/2020
Mọi người giúp e với ạ. Em cảm ơn
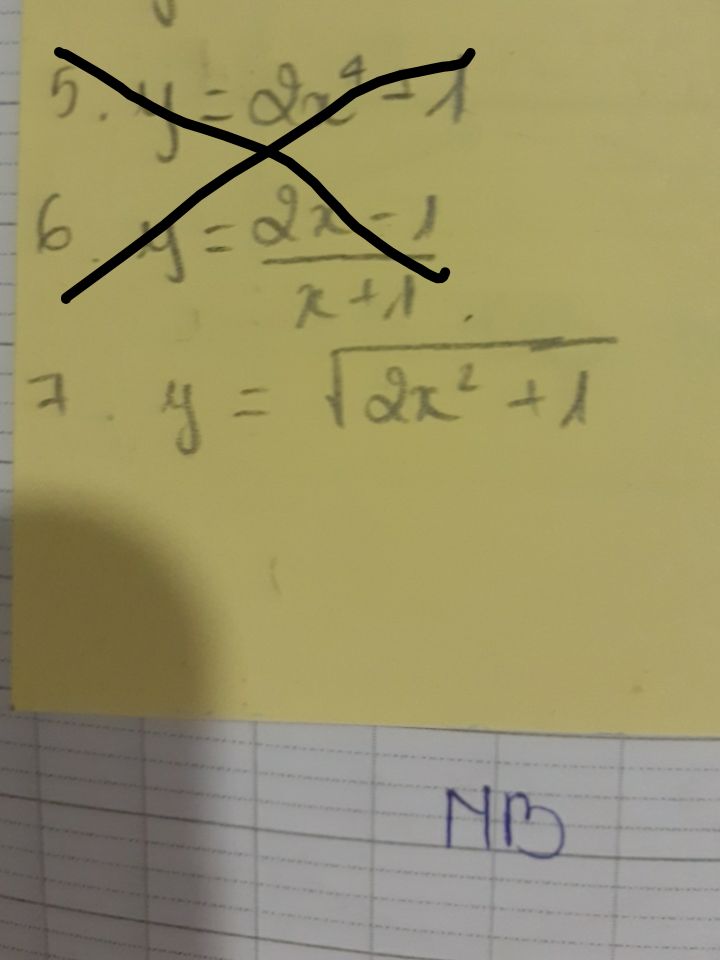 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tất cả các giá trị thực của m để hàm số \(y=\dfrac{x+3}{x+m}\) đồng biến trên khoảng \((-\infty ; -6)\)?
bởi Trần Phước Trường Vũ
 09/08/2020
09/08/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Khảng định nào sau đây là đúng?
bởi Trang Thư
 09/08/2020
09/08/2020
Câu 13 ạ
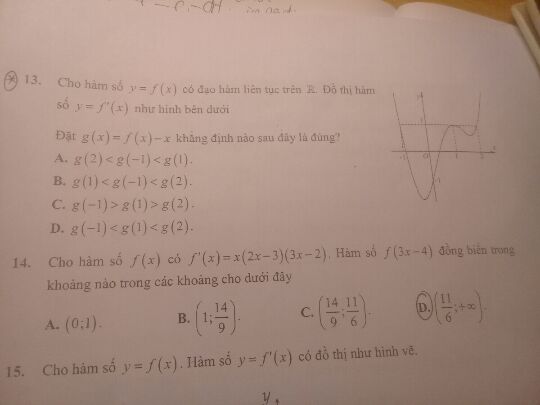 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm tất cả giá trị thực của m để hàm số \(y=(m^2+ m +1)x+ (m^2-m +1)\sin x\) luôn đồng biến trên (0;2π)?
bởi hung2k3
 09/08/2020
Theo dõi (1) 0 Trả lời
09/08/2020
Theo dõi (1) 0 Trả lời -


Hàm số dưới đây nghịch biến trên khoảng nào?
bởi BT
 07/08/2020
07/08/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời
Bài tập SGK khác
Bài tập 1.2 trang 7 SBT Toán 12
Bài tập 1.3 trang 8 SBT Toán 12
Bài tập 1.5 trang 8 SBT Toán 12
Bài tập 1.6 trang 8 SBT Toán 12
Bài tập 1.7 trang 8 SBT Toán 12
Bài tập 1.8 trang 8 SBT Toán 12
Bài tập 1.9 trang 8 SBT Toán 12
Bài tập 1.10 trang 8 SBT Toán 12
Bài tập 1.11 trang 9 SBT Toán 12
Bài tập 1.12 trang 9 SBT Toán 12
Bài tập 1.13 trang 9 SBT Toán 12
Bài tập 1.14 trang 9 SBT Toán 12
Bài tập 1.15 trang 9 SBT Toán 12
Bài tập 1.16 trang 9 SBT Toán 12
Bài tập 1 trang 7 SGK Toán 12 NC
Bài tập 2 trang 7 SGK Toán 12 NC
Bài tập 3 trang 8 SGK Toán 12 NC
Bài tập 4 trang 8 SGK Toán 12 NC
Bài tập 5 trang 8 SGK Toán 12 NC
Bài tập 6 trang 8 SGK Toán 12 NC
Bài tập 7 trang 8 SGK Toán 12 NC
Bài tập 8 trang 8 SGK Toán 12 NC





