Giải bài 3 tr 17 sách GK Toán Hình lớp 10
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho \( \overrightarrow{MB}=3\overrightarrow{MC}\). Hãy phân tích vectơ \(\overrightarrow{AM}\) theo hai vectơ \(\overrightarrow{u}=\overrightarrow{AB}, \overrightarrow{v}=\overrightarrow{AC}\).
Hướng dẫn giải chi tiết bài 3
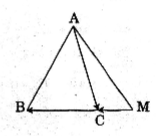
Ta có: \(\overrightarrow {AM} = \overrightarrow {AC} + \overrightarrow {CM} \,\,\,\,\,\,\,\,\,(1)\)
Vì \(\overrightarrow {CM} \) cùng hướng với \(\overrightarrow {BC} ,\) hơn nữa \(\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {CM} } \right|,\) nên
\(\overrightarrow {CM} = \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}(\overrightarrow {AC} - \overrightarrow {AB} )\,\,\,\,\,\,(2)\)
Từ (1) và (2) ta có:
\(\overrightarrow {AM} = \overrightarrow {AC} + \frac{1}{2}(\overrightarrow {AC} - \overrightarrow {AB} ) \Leftrightarrow \overrightarrow {AM} = \frac{3}{2}\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} .\)
Vậy \(\overrightarrow {AM} = \frac{3}{2}\vec v - \frac{1}{2}\vec u.\)
-- Mod Toán 10 HỌC247
-


Cho tam giác \(ABC\) và ba vec tơ cố định \(\overrightarrow u ,\,\overrightarrow v ,\,\overrightarrow w \). Với mỗi số thực \(t\), ta lấy các điểm \(A’, B’, C’\) sao cho \(\overrightarrow {AA'} = t\overrightarrow u \,;\,\,\overrightarrow {BB'} = t\overrightarrow v \,;\,\,\overrightarrow {CC'} = t\overrightarrow w \). Tìm quỹ tích trọng tâm \(G’\) của hai tam giác \(A’B’C’\) khi \(t\) thay đổi.
bởi Anh Thu
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho điểm \(O\) cố định và hai vec tơ \(\overrightarrow u \,,\,\overrightarrow v \) cố định. Với mỗi số \(m\) ta xác định điểm \(M\) sao cho \(\overrightarrow {OM} = m\overrightarrow u + (1 - m)\overrightarrow v \). Tìm tập hợp các điểm \(M\) khi \(m\) thay đổi.
bởi Mai Đào
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho điểm \(O\) cố định và đường thẳng \(d\) đi qua hai điểm \(A, B\) cố định. Chứng minh rằng điểm M thuộc đường thẳng \(d\) khi và chỉ khi có số \(\alpha \) sao cho \(\overrightarrow {OM} = \alpha \overrightarrow {OA} + (1 - \alpha )\overrightarrow {OB} \). Với điều kiện nào của \(\alpha \) thì \(M\) thuộc đoạn thẳng \(AB\)?
bởi thi trang
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho hai điểm phân biệt \(A, B\). Hãy xác định các điểm \(P, Q, R\), biết: \(2\overrightarrow {PA} + 3\overrightarrow {PB} = \overrightarrow 0;\) \(- 2\overrightarrow {QA} + \overrightarrow {QB} = \overrightarrow 0 ;\) \(\overrightarrow {RA} - 3\overrightarrow {RB} = \overrightarrow 0 \)
bởi Huong Hoa Hồng
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 17 SGK Hình học 10
Bài tập 2 trang 17 SGK Hình học 10
Bài tập 4 trang 17 SGK Hình học 10
Bài tập 5 trang 17 SGK Hình học 10
Bài tập 6 trang 17 SGK Hình học 10
Bài tập 7 trang 17 SGK Hình học 10
Bài tập 8 trang 17 SGK Hình học 10
Bài tập 9 trang 17 SGK Hình học 10
Bài tập 1.20 trang 31 SBT Hình học 10
Bài tập 1.21 trang 35 SBT Hình học 10
Bài tập 1.22 trang 31 SBT Hình học 10
Bài tập 1.23 trang 31 SBT Hình học 10
Bài tập 1.24 trang 31 SBT Hình học 10
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC





