Bài tập 22 trang 24 SGK Toán 10 NC
Cho tam giác OAB. Gọi M, N lần lượt là trung điểm hai cạnh OA và OB. Hãy tìm các số m và n thích hợp trong mỗi đẳng thức sau đây:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OM} = m\overrightarrow {OA} + n\overrightarrow {OB} \\
\overrightarrow {MN} = m\overrightarrow {OA} + n\overrightarrow {OB}
\end{array}\\
\begin{array}{l}
\overrightarrow {AN} = m\overrightarrow {OA} + n\overrightarrow {OB} \\
\overrightarrow {MB} = m\overrightarrow {OA} + n\overrightarrow {OB.}
\end{array}
\end{array}\)
Hướng dẫn giải chi tiết
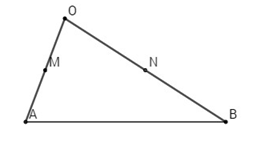
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OM} = \frac{1}{2}\overrightarrow {OA} = \frac{1}{2}\overrightarrow {OA} + 0.\overrightarrow {OB} \\
\Rightarrow m = \frac{1}{2},n = 0
\end{array}\\
{\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = \frac{1}{2}\overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} }\\
{ = \left( { - \frac{1}{2}} \right)\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \Rightarrow m = - \frac{1}{2},n = \frac{1}{2}}\\
{\overrightarrow {AN} = \overrightarrow {ON} - \overrightarrow {OA} = \frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} }\\
{ = \left( { - 1} \right)\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \Rightarrow m = - 1,n = \frac{1}{2}{\mkern 1mu} }\\
{\overrightarrow {MB} = \overrightarrow {OB} - \overrightarrow {OM} = \overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} }\\
{ = \left( { - \frac{1}{2}} \right)\overrightarrow {OA} + \overrightarrow {OB} \Rightarrow m = - \frac{1}{2},n = 1}
\end{array}\)
-- Mod Toán 10 HỌC247
-


Cho tam giác ABC nội tiếp trong đường tròn tâm O. Gọi G và H theo thứ tự là trọng tâm và trực tâm của tam giác. Chứng minh rằng
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)
Từ đó chứng minh G,H, O thẳng hàng.
Theo dõi (0) 1 Trả lời






