Giải bài 9 tr 17 sách GK Toán Hình lớp 10
Cho tam giác đều ABC có trọng tâm O và M là một điểm tùy ý trong tam giác. Gọi D,E,F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng: \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF} =\frac{3}{2}\overrightarrow{MO}\)
Hướng dẫn giải chi tiết bài 9
Ta có:
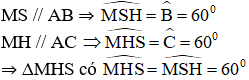
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
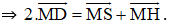
Chứng minh tương tự ta có:
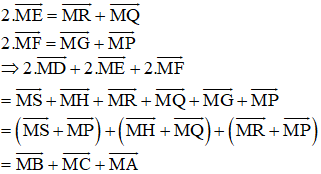
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
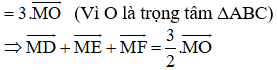
-- Mod Toán 10 HỌC247
-
Tìm giá trị của \(m\) sao cho \(\overrightarrow a = m\overrightarrow b \) trong trường hợp sau: \(\overrightarrow a \ne \overrightarrow 0 ,\overrightarrow b = \overrightarrow 0 \)
bởi sap sua
21/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị của \(m\) sao cho \(\overrightarrow a = m\overrightarrow b \) trong trường hợp sau: \(\overrightarrow a = \overrightarrow 0 ,\overrightarrow b \ne \overrightarrow 0 \).
bởi Ban Mai
21/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị của \(m\) sao cho \(\overrightarrow a = m\overrightarrow b \) trong trường hợp sau: \(\overrightarrow a ,\overrightarrow b \) ngược hướng và \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 15\).
bởi Trần Bảo Việt
21/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị của \(m\) sao cho \(\overrightarrow a = m\overrightarrow b \) trong trường hợp sau: \(\overrightarrow a ,\overrightarrow b \) cùng hướng và \(\left| {\overrightarrow a } \right| = 20,\left| {\overrightarrow b } \right| = 5\)
bởi Hoa Hong
22/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 17 SGK Hình học 10
Bài tập 8 trang 17 SGK Hình học 10
Bài tập 1.20 trang 31 SBT Hình học 10
Bài tập 1.21 trang 35 SBT Hình học 10
Bài tập 1.22 trang 31 SBT Hình học 10
Bài tập 1.23 trang 31 SBT Hình học 10
Bài tập 1.24 trang 31 SBT Hình học 10
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
