Giải bài 1.27 tr 31 SBT Hình học 10
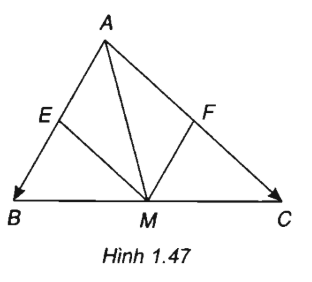
Cho tam giác ABC có trung tuyến \(\overrightarrow {AM} \) (M là trung điểm của BC). Phân tích vec tơ \(\overrightarrow {AM} \) theo hai vec tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
Hướng dẫn giải chi tiết
Gọi E, F lần lượt là trung điểm của AB, AC.
Ta có tứ giác AFME là hình bình hành nên \(\overrightarrow {AM} = \overrightarrow {AE} + \overrightarrow {AF} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \).
-- Mod Toán 10 HỌC247
-


cho ngũ giác ABCDE . Chứng minh :
a) vecto AB + vecto CD = vecto AE - vecto BC - vecto DE
b) vecto AB = vecto AC - vecto DC - vecto BE - vecto ED
Theo dõi (0) 1 Trả lời -


Tìm tập hợp điểm M thỏa |3vt MA-2vt MC|=|vt MB-vt MC|
bởi Truc Ly
 13/10/2018
13/10/2018
Cho tam giác ABC, tìm tập hợp những điểm M thỏa mãn:
\(\left|3\overrightarrow{MA}-2\overrightarrow{MC}\right|=\left|\overrightarrow{MB}-\overrightarrow{MC}\right|\)
Theo dõi (0) 1 Trả lời -


Chứng minh vt IM + vt IN + vt IP=1/2(vt IA + vt IB + vt IC + vt ID + vt IE + vt IF) với mọi I
bởi thùy trang
 13/10/2018
13/10/2018
Cho lục giác đều ABCDEF có M,N,P lần lượt là trung điểm của AB,CD,EF
a. Chứng minh : vt IM + vt IN + vt IP=1/2(vt IA + vt IB + vt IC + vt ID + vt IE + vt IF) với mọi I
b. Tìm G để vt GA + vt GB + vt GC + vt GD + vt GE + vt GF=vt 0
c. Gọi G1,G2,G3,G4,G5,G6 lần lượt là trọng tâm của tam giác ABC , tam giác DEF , tam giác BCD , tam giác EFA , tam giác CDE , tam giác FAB. Chứng minh G1G2 , G3G4 , G5G6 đồngTheo dõi (0) 1 Trả lời -


Các bạn làm ơn giúp mình câu này với: Cho tam giác ABC. Tìm tập hợp các điểm M thỏa:
\(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC