Giải bài 1.30 tr 32 SBT Hình học 10
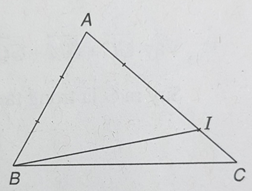
Cho tam giác ABC. Điểm I trên cạnh AC sao cho \(CI = \frac{1}{4}CA\), J là điểm mà \(\overrightarrow {BJ} = \frac{1}{2}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} \).
a) Chứng minh \(\overrightarrow {BI} = \frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \).
b) Chứng minh B, I, J thẳng hàng.
c) Hãy dựng điểm J thỏa mãn điều kiện đề bài.
Hướng dẫn giải chi tiết
a) \(\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} = - \overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \)
b) Ta có: \(\frac{2}{3}\overrightarrow {BI} = \frac{2}{3}\left( {\frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{2}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} = \overrightarrow {BJ} \)
Vậy \(\overrightarrow {BJ} = \frac{2}{3}\overrightarrow {BI} \) hay ba điểm B, J, I thẳng hàng.
c) Do \(\overrightarrow {BJ} = \frac{2}{3}\overrightarrow {BI} \) nên ta dựng được hình như hình vẽ trên.
-- Mod Toán 10 HỌC247
-


cho tam giác ABC tìm điểm J sao cho vecto JA-JB-2JC=0
Theo dõi (0) 1 Trả lời -


Xác định điểm M để |vt MA+vt MB|=căn 3
bởi na na
 23/10/2018
23/10/2018
Cho đoạn thẳng AB, xát định điểm M sao cho |\(\overrightarrow{MA}\)+\(\overrightarrow{MB}\)|=\(\sqrt{3}\)
Theo dõi (0) 1 Trả lời -


giúp mình với nhá
cho hình bình hành abcd có tâm o. hãy xác định các điểm i,f,k thỏa mãn đẳng thức :
a) vecto IA+ vecto IB + vecto IC =4 vecto ID
b) 2vecto FA +2 vecto FB = 3 vecto FC - vecto FD
c)4 vecto KA +3 vecto KB +2 vecto KC + vecto KD = vecto 0
Theo dõi (0) 1 Trả lời -


Chứng minh |vt MA_1+vt MA_2+...+vt MA_2014-2014.vt MA_2015| không phụ thuộc điểm M
bởi hi hi
 23/10/2018
23/10/2018
trong mặt phẳng cho20015 điểm A1,A2,...,A2015 cố định và điểm M thay đổi .cm
\(|\overrightarrow{MA_1}+\overrightarrow{MA_2}+....+\overrightarrow{MA_{2014}}-2014\overrightarrow{MA_{2015}}|\) không phụ thuộc vào vị trí điểm M
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC