Giải bài 1.24 tr 31 SBT Hình học 10
Cho hai tam giác ABC và A′B′C′. Chứng minh rằng nếu \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0\) thì hai tam giác đó có cùng trọng tâm.
Hướng dẫn giải chi tiết
Gọi G và G′ lần lượt là trọng tâm của hai tam giác ABC và A′B′C′. Ta có:
\(\begin{array}{l}
\overrightarrow {AA'} = \overrightarrow {AG} + \overrightarrow {GG'} + \overrightarrow {G'A'} \\
\overrightarrow {BB'} = \overrightarrow {BG} + \overrightarrow {GG'} + \overrightarrow {G'B'} \\
\overrightarrow {CC'} = \overrightarrow {CG} + \overrightarrow {GG'} + \overrightarrow {GC'}
\end{array}\)
Cộng từng vế của ba đẳng thức trên ta được:
\(\begin{array}{l}
\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) + 3\overrightarrow {GG'} + \left( {\overrightarrow {G'A'} + \overrightarrow {G'B'} + \overrightarrow {G'C'} } \right)\\
= \overrightarrow 0 + 3\overrightarrow {GG'} + \overrightarrow 0 = 3\overrightarrow {GG'}
\end{array}\)
Do đó, nếu \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0\) thì \(\overrightarrow {GG'} = \overrightarrow 0 \) hay G ≡ G′
Chú ý: Từ chứng minh trên cũng suy ra rằng nếu hai tam giác ABC và A′B′C′ có cùng trọng tâm thì \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0\)
-- Mod Toán 10 HỌC247
-


Tìm đẳng thức đúng biết ABCD là hình bình hành, M, N là trung điểm của BC và CD
bởi Hân Ngọc
 06/01/2020
Mong các thầy cô và các bạn giúp e
06/01/2020
Mong các thầy cô và các bạn giúp e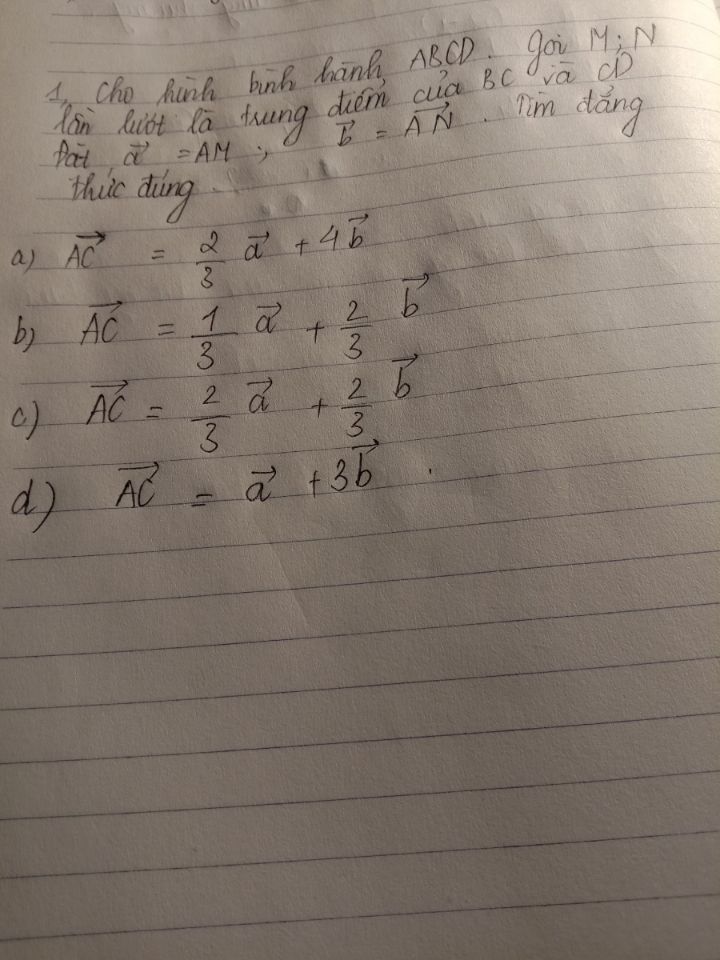 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tính vectơ CI theo vt a va vt b vt la vecto
bởi Nguyễn Thị Thanh Hoài
 30/11/2019
Giúp mk vs ạTheo dõi (1) 0 Trả lời
30/11/2019
Giúp mk vs ạTheo dõi (1) 0 Trả lời -

 Cho hình bình hành ABCD tâm O, I là tr ui sẽung điểm của BO. Hãy biểu diễn vectơ AI theo vectơ AB và ADTheo dõi (1) 0 Trả lời
Cho hình bình hành ABCD tâm O, I là tr ui sẽung điểm của BO. Hãy biểu diễn vectơ AI theo vectơ AB và ADTheo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 1.22 trang 31 SBT Hình học 10
Bài tập 1.23 trang 31 SBT Hình học 10
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC





