Bài tập 21 trang 23 SGK Hình học 10 NC
Cho tam giác vuông cân OAB với OA = OB = a. Hãy dựng các vec tơ sau đây và tính độ dài của chúng
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} ;\\
\overrightarrow {OA} - \overrightarrow {OB} ;\\
3\overrightarrow {OA} + 4\overrightarrow {OB} ;\\
\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} ;\\
\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} .
\end{array}\)
Hướng dẫn giải chi tiết
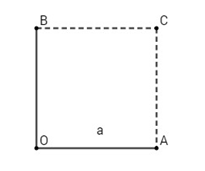
Vẽ hình vuông OACB, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \\
\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = a\sqrt 2
\end{array}\\
\begin{array}{l}
\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \\
\Rightarrow \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right| = \left| {\overrightarrow {BA} } \right| = a\sqrt 2
\end{array}
\end{array}\)
Gọi M, N là điểm thỏa mãn:
\(\overrightarrow {OM} = 3\overrightarrow {OA} ,\overrightarrow {ON} = 4\overrightarrow {OB} \)
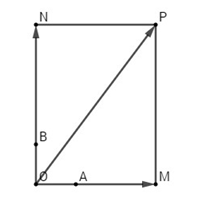
Vẽ hình chữ nhật MONP, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OM} + \overrightarrow {ON} = {\mkern 1mu} \overrightarrow {OP} \\
\Rightarrow \left| {\overrightarrow {OM} + \overrightarrow {ON} } \right| = \left| {\overrightarrow {OP} } \right|\\
= \sqrt {O{M^2} + O{N^2}}
\end{array}\\
{ = \sqrt {9{a^2} + 16{a^2}} = 5a}
\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}
\left| {\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} } \right|\\
= \sqrt {{{\left( {\frac{{21}}{4}a} \right)}^2} + {{\left( {\frac{5}{2}a} \right)}^2}} \\
= \frac{{\sqrt {241} }}{4}a
\end{array}\)
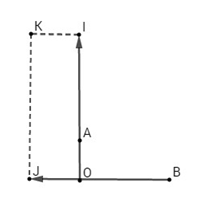
Gọi I, J là điểm thỏa mãn:
\(\overrightarrow {OI} = \frac{{11}}{4}\overrightarrow {OA} ;\overrightarrow {OJ} = - \frac{3}{7}\overrightarrow {OB} \)
Vẽ hình chữ nhật OIKJ, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} = \frac{{11}}{4}\overrightarrow {OA} + \left( { - \frac{3}{7}} \right)\overrightarrow {OB} \\
= \overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow {OK}
\end{array}\\
\begin{array}{l}
\Rightarrow \left| {\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} } \right| = \left| {\overrightarrow {OK} } \right|\\
= \sqrt {{{\left( {\frac{{11}}{4}a} \right)}^2} + {{\left( { - \frac{3}{7}a} \right)}^2}} = \frac{{\sqrt {6073} }}{{28}}a
\end{array}
\end{array}\)
-- Mod Toán 10 HỌC247
-


Cho tam giác ABC nội tiếp trong đường tròn tâm O. Gọi G và H theo thứ tự là trọng tâm và trực tâm của tam giác. Chứng minh rằng
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)
Từ đó chứng minh G,H, O thẳng hàng.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC






